Modul 2 Praktikum Persamaan Diferensial Biasa: Metode Taylor Orde n dan Runge-Kutta

Kembali ke Praktikum Persamaan Diferensial Biasa

Metode Taylor orde \(n\)

Metode Taylor orde \(n\) adalah perluasan dari metode Euler (di mana metode Taylor orde 1 sama saja dengan metode Euler). Rumus iterasinya bisa ditulis sebagai berikut:

\[w_1 = \alpha\]

\[\begin{align*} T^{(n)} \left(t_i, w_i\right) &= f\left(t_i, w_i\right) + \frac{h}{2}f'\left(t_i, w_i\right) + \cdots + \frac{h^{n-1}}{n!} f^{\left(n-1\right)} \left(t_i,w_i\right) \\ \end{align*}\]

\[w_{i+1} = w_i + hT^{(n)} \left(t_i, w_i\right) \]

Perhatikan bahwa, dengan metode Taylor orde \(n\), kita perlu memperoleh terlebih dahulu rumus analitik untuk sejumlah turunan (terhadap \(t\)) dari \(f\left(t_i, w_i\right)\) yaitu \(f', f'', \dots, f^{(n-1)}\).

Kebetulan, untuk metode Euler, yaitu metode Taylor orde 1 (\(n=1\)), kita tidak perlu menghitung turunan fungsinya sama sekali.

Untuk mempermudah pemrograman, kita coba tulis ulang rumus \(T^{(n)} \left(t_i, w_i\right)\) dengan sumasi:

\[\begin{align*} T^{(n)} \left(t_i, w_i\right) &= f\left(t_i, w_i\right) + \frac{h}{2}f'\left(t_i, w_i\right) + \cdots + \frac{h^{n-1}}{n!} f^{\left(n-1\right)} \left(t_i,w_i\right) \\ &= \sum_{j=1}^{n} \frac{h^{j-1}}{j!} f^{\left(j-1\right)} \left(t_i,w_i\right) \\ &= f\left(t_i,w_i\right) + \sum_{j=2}^{n} \frac{h^{j-1}}{j!} f^{\left(j-1\right)} \left(t_i,w_i\right) \end{align*}\]

Dengan demikian, kita bisa menyimpan fungsi-fungsi \(f', f'', \dots, f^{(n-1)}\) di dalam suatu cell array, misal dinamakan fp, sehingga

• kita bisa mengakses turunan ke-\(i\) dengan menulis fp{i}
• orde \(n\) untuk metode Taylor bisa ditentukan menggunakan panjang cell array tersebut, yaitu n = length(fp) + 1;
• jika cell array kosong (tidak ada fungsi turunan), otomatis \(n=1\) dan algoritmanya menjadi sama saja dengan metode Euler (sesuai harapan)
• penjumlahannya bisa menggunakan for loop sederhana
• kita cukup mendefinisikan fungsi metode Taylor ini sekali saja di Octave, daripada harus membuat definisi terpisah untuk orde 2, orde 3, orde 4, dan seterusnya (di mana banyaknya fungsi turunan memang berbeda)

Secara keseluruhan, metode Taylor orde \(n\) dapat ditulis sebagai berikut.

\[w_1 = \alpha\]

\[w_{i+1} = w_i + hT^{(n)} \left(t_i, w_i\right)\]

\[T^{(n)} \left(t_i, w_i\right) = f\left(t_i,w_i\right) + \sum_{j=2}^{n} \frac{h^{j-1}}{j!} f^{\left(j-1\right)} \left(t_i,w_i\right)\]

Perhatikan bahwa metode Taylor orde 1 adalah metode Euler pada pertemuan sebelumnya.

Function file taylor.m - nama file harus sama dengan nama fungsi

function [t, w] = taylor(f, fp, a, b, N, alpha)
  h = (b - a) / N;
  n = length(fp) + 1;
  t = zeros(n + 1, 1);
  w = zeros(n + 1, 1);
  t(1) = a;
  w(1) = alpha;
  for i = 1 : N
    t(i + 1) = t(i) + h;
    
    T = f(t(i), w(i));
    for j = 2 : n
      T += h^(j-1) * fp{j-1}(t(i),w(i)) / factorial(j);
    endfor
    
    w(i + 1) = w(i) + h * T;
  endfor
endfunction

Misalkan diberikan MNA sebagai berikut, yang diminta untuk diselesaikan secara numerik dengan metode Taylor orde 4:

\[y' = y - t^2 + 1\] \[0 \le t \le 2\] \[y(0) = 0.5\]

Maka, dengan \(y' = f\left(t, y\right) = y - t^2 + 1\), bisa dihitung:

\[f'\left(t, y\right) = y - t^2 + 1 - 2t\]

\[f''\left(t, y\right) = y - t^2 - 2t - 1\]

\[f^{(3)}\left(t, y\right) = y - t^2 - 2t - 1, \hspace{0.2cm} \text{kebetulan sama persis dengan} \hspace{0.2cm} f''\left(t, y\right)\]

Script file coba_taylor4.m - nama file bebas

% contoh pakai: subbab 5.3 example 1b (orde 4)

% f(t_i, w_i)
f0 = @(t,y) y - t^2 + 1;

% f'(t_i, w_i)
f1 = @(t,y) y - t^2 + 1 - 2*t;

% f''(t_i, w_i)
f2 = @(t,y) y - t^2 - 2*t - 1;

% f'''(t_i, w_i)
f3 = @(t,y) y - t^2 - 2*t - 1;

% hitung pada interval [0,2], N=10, y(0)=alpha=0.5
[t, w] = taylor(f0, {f1, f2, f3}, 0, 2, 10, 0.5);
% otomatis Taylor orde 4 karena
% ada tiga fungsi turunan f1, f2, f3
% yang diinput di cell array

% bandingkan dengan Tabel 5.4
[t, w]

ans =

        0   0.5000
   0.2000   0.8293
   0.4000   1.2141
   0.6000   1.6489
   0.8000   2.1272
   1.0000   2.6409
   1.2000   3.1800
   1.4000   3.7324
   1.6000   4.2835
   1.8000   4.8152
   2.0000   5.3056

Kita bisa membandingkan antara solusi eksak, metode Euler, dan metode Taylor orde 4, baik dalam menampilkan tabel iterasi maupun menampilkan plot:

Script file bandingkan_taylor.m - nama file bebas

% fungsi f(t,y) dan turunan pertama, kedua, ketiga
f0 = @(t,y) y - t^2 + 1;
f1 = @(t,y) y - t^2 + 1 - 2*t;
f2 = @(t,y) y - t^2 - 2*t - 1;
f3 = @(t,y) y - t^2 - 2*t - 1;

a = 0;
b = 2;
N = 10;
alpha = 0.5;

% menghitung metode Euler dan metode Taylor orde 4
[t_euler, w_euler] = euler(f0, a, b, N, alpha);
[t_taylor, w_taylor] = taylor(f0, {f1,f2,f3}, a, b, N, alpha);

% solusi eksak
sln = @(t) (t + 1).^2 - 0.5 * exp(t);
y_eksak = sln(t_euler);

% tampilkan tabel
[t_euler, w_euler, w_taylor, y_eksak]

% plotting
hold on;
fplot(sln, [a, b], 'b');
scatter(t_euler, w_euler, 'r');
scatter(t_taylor, w_taylor, 'g');
legend("Solusi Eksak", "Metode Euler", "Metode Taylor orde 4");

ans =

        0   0.5000   0.5000   0.5000
   0.2000   0.8000   0.8293   0.8293
   0.4000   1.1520   1.2141   1.2141
   0.6000   1.5504   1.6489   1.6489
   0.8000   1.9885   2.1272   2.1272
   1.0000   2.4582   2.6409   2.6409
   1.2000   2.9498   3.1800   3.1799
   1.4000   3.4518   3.7324   3.7324
   1.6000   3.9501   4.2835   4.2835
   1.8000   4.4282   4.8152   4.8152
   2.0000   4.8658   5.3056   5.3055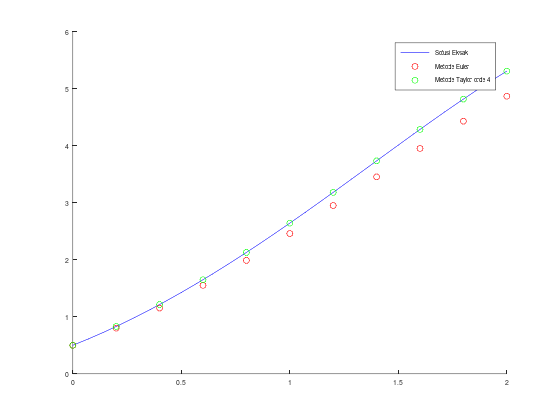

Output Octave

Metode Runge-Kutta dan variasinya

Orde 2: Metode Midpoint

\[w_1=\alpha\] \[w_{i+1}=w_i+h f\left(t_i+\frac{h}{2}, w_i+\frac{h}{2} f\left(t_i, w_i\right)\right)\]

bisa juga ditulis,

\[w_1=\alpha\] \[m_1 = f\left(t_i, w_i\right)\] \[w_{i+1}=w_i+h f\left(t_i+\frac{h}{2}, w_i+\frac{h}{2} m_1\right)\]

atau bahkan,

\[w_1=\alpha\] \[m_1 = f\left(t_i, w_i\right)\] \[m_2 = f\left(t_i+\frac{h}{2}, w_i+\frac{h}{2} m_1\right)\] \[w_{i+1}=w_i+h m_2\]

Function file midpoint.m - nama file harus sama dengan nama fungsi

function [t, w] = midpoint(f, a, b, N, alpha)
  h = (b - a) / N;
  t = zeros(N + 1, 1);
  w = zeros(N + 1, 1);
  t(1) = a;
  w(1) = alpha;
  for i = 1 : N
    t(i + 1) = t(i) + h;
    m1 = f(t(i), w(i));
    m2 = f(t(i) + (h / 2), w(i) + (h / 2) * m1);
    w(i + 1) = w(i) + h * m2;
  endfor
endfunction

Misalkan diberikan MNA sebagai berikut, yang ingin diselesaikan secara numerik dengan \(N = 10\):

\[y' = y - t^2 + 1\] \[0 \le t \le 2\] \[y(0) = 0.5\]

yang kebetulan memiliki solusi eksak:

\[y\left(t\right) = \left( t + 1 \right)^2 - 0.5 e^t\]

Contoh penggunaan:

Script file coba_midpoint.m - nama file bebas

f = @(t, y) (y - t .^ 2 + 1);
a = 0;
b = 2;
N = 10;
alpha = 0.5;

[t, w] = midpoint(f, a, b, N, alpha);

sln = @(t) (t + 1) .^ 2 - 0.5 * exp(t);
y_eksak = sln(t);

err_midpoint = abs(w - y_eksak);
err_midpoint_total = sum(err_midpoint); % norm L1 (taxicab/Manhattan)

disp("Tabel aproksimasi w, solusi eksak y, dan error:");
[t, w, y_eksak, err_midpoint]
disp("Error total (norm L1):");
disp(err_midpoint_total);

hold on;
fplot(sln, [a, b], 'b');
scatter(t, w, 'r');
legend("Solusi Eksak", "Metode Midpoint");

Tabel aproksimasi w, solusi eksak y, dan error:
ans =

        0   0.5000   0.5000        0
   0.2000   0.8280   0.8293   0.0013
   0.4000   1.2114   1.2141   0.0027
   0.6000   1.6447   1.6489   0.0043
   0.8000   2.1213   2.1272   0.0059
   1.0000   2.6332   2.6409   0.0077
   1.2000   3.1705   3.1799   0.0095
   1.4000   3.7212   3.7324   0.0112
   1.6000   4.2706   4.2835   0.0129
   1.8000   4.8010   4.8152   0.0142
   2.0000   5.2904   5.3055   0.0151

Error total (norm L1):
0.084840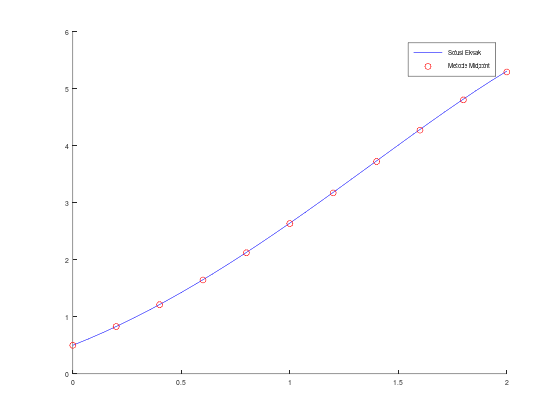

Orde 2: Metode Modified Euler

\[w_1=\alpha\] \[w_{i+1}=w_i+\frac{h}{2}\left(f\left(t_i, w_i\right)+f\left(t_{i+1}, w_i+h f\left(t_i, w_i\right)\right)\right)\]

bisa juga ditulis,

\[w_1=\alpha\] \[m_1 = f\left(t_i, w_i\right)\] \[w_{i+1}=w_i+\frac{h}{2}\left(m_1+f\left(t_{i+1}, w_i+h m_1\right)\right)\]

atau bahkan,

\[w_1=\alpha\] \[m_1 = f\left(t_i, w_i\right)\] \[m_2 = f\left(t_{i+1}, w_i+h m_1\right)\] \[w_{i+1}=w_i+\frac{h}{2}\left(m_1+m_2\right)\]

Function file modified_euler.m - nama file harus sama dengan nama fungsi

function [t, w] = modified_euler(f, a, b, N, alpha)
  h = (b - a) / N;
  t = zeros(N + 1, 1);
  w = zeros(N + 1, 1);
  t(1) = a;
  w(1) = alpha;
  for i = 1 : N
    t(i + 1) = t(i) + h;
    m1 = f(t(i), w(i));
    m2 = f(t(i + 1), w(i) + h * m1);
    w(i + 1) = w(i) + h * (m1 + m2) / 2;
  endfor
endfunction

Misalkan diberikan MNA sebagai berikut, yang ingin diselesaikan secara numerik dengan \(N = 10\):

\[y' = y - t^2 + 1\] \[0 \le t \le 2\] \[y(0) = 0.5\]

dan misalkan solusi eksak tidak diketahui.

Contoh penggunaan (perbandingan metode Runge-Kutta orde 2):

Script file bandingkan_rko2.m - nama file bebas

f = @(t, y) (y - t .^ 2 + 1);
a = 0;
b = 2;
N = 10;
alpha = 0.5;

[t1, w1] = midpoint(f, a, b, N, alpha);
[t2, w2] = modified_euler(f, a, b, N, alpha);

[t1, w1, w2]

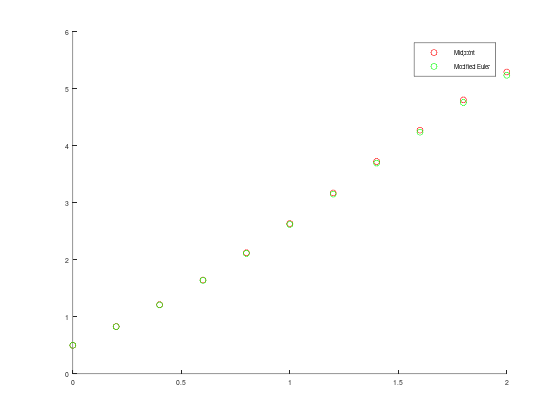
hold on;
scatter(t1, w1, 'r');
scatter(t2, w2, 'g');
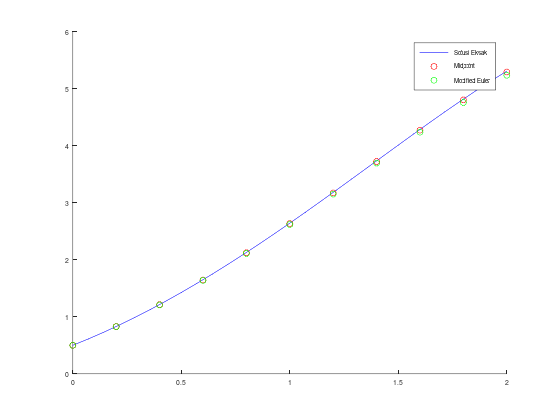
legend("Midpoint", "Modified Euler");

ans =

        0   0.5000   0.5000
   0.2000   0.8280   0.8260
   0.4000   1.2114   1.2069
   0.6000   1.6447   1.6372
   0.8000   2.1213   2.1102
   1.0000   2.6332   2.6177
   1.2000   3.1705   3.1496
   1.4000   3.7212   3.6937
   1.6000   4.2706   4.2351
   1.8000   4.8010   4.7556
   2.0000   5.2904   5.2331

Misalkan diketahui solusi eksak:

\[y\left(t\right) = \left( t + 1 \right)^2 - 0.5 e^t\]

Maka kita juga bisa menghitung error dari masing-masing metode.

Script file bandingkan2_rko2.m - nama file bebas

f = @(t, y) (y - t .^ 2 + 1);
a = 0;
b = 2;
N = 10;
alpha = 0.5;

[t1, w1] = midpoint(f, a, b, N, alpha);
[t2, w2] = modified_euler(f, a, b, N, alpha);

sln = @(t) (t + 1) .^ 2 - 0.5 * exp(t);
y_eksak = sln(t1);

err1 = abs(y_eksak - w1);
err2 = abs(y_eksak - w2);

[t1, y_eksak, w1, err1, w2, err2]

hold on;
fplot(sln, [a, b], 'b');
scatter(t1, w1, 'r');
scatter(t2, w2, 'g');
legend("Solusi Eksak", "Midpoint", "Modified Euler");

ans =

        0   0.5000   0.5000        0   0.5000        0
   0.2000   0.8293   0.8280   0.0013   0.8260   0.0033
   0.4000   1.2141   1.2114   0.0027   1.2069   0.0072
   0.6000   1.6489   1.6447   0.0043   1.6372   0.0117
   0.8000   2.1272   2.1213   0.0059   2.1102   0.0170
   1.0000   2.6409   2.6332   0.0077   2.6177   0.0232
   1.2000   3.1799   3.1705   0.0095   3.1496   0.0304
   1.4000   3.7324   3.7212   0.0112   3.6937   0.0387
   1.6000   4.2835   4.2706   0.0129   4.2351   0.0484
   1.8000   4.8152   4.8010   0.0142   4.7556   0.0596
   2.0000   5.3055   5.2904   0.0151   5.2331   0.0724

Orde 3: Metode Heun

\[w_1=\alpha\] \[w_{i+1}=w_i+\frac{h}{4}\left(f\left(t_i, w_i\right)+3 f\left(t_i+\frac{2 h}{3}, w_i+\frac{2 h}{3} f\left(t_i+\frac{h}{3}, w_i+\frac{h}{3} f\left(t_i, w_i\right)\right)\right)\right)\]

bisa juga ditulis,

\[w_1=\alpha\] \[m_1 = f\left(t_i, w_i\right)\] \[w_{i+1}=w_i+\frac{h}{4}\left(m_1+3 f\left(t_i+\frac{2 h}{3}, w_i+\frac{2 h}{3} f\left(t_i+\frac{h}{3}, w_i+\frac{h}{3} m_1\right)\right)\right)\]

atau,

\[w_1=\alpha\] \[m_1 = f\left(t_i, w_i\right)\] \[m_2 = f\left(t_i+\frac{h}{3}, w_i+\frac{h}{3} m_1\right)\] \[w_{i+1}=w_i+\frac{h}{4}\left(m_1+3 f\left(t_i+\frac{2 h}{3}, w_i+\frac{2 h}{3} m_2\right)\right)\]

atau bahkan,

\[w_1=\alpha\] \[m_1 = f\left(t_i, w_i\right)\] \[m_2 = f\left(t_i+\frac{h}{3}, w_i+\frac{h}{3} m_1\right)\] \[m_3 = f\left(t_i+\frac{2 h}{3}, w_i+\frac{2 h}{3} m_2\right)\] \[w_{i+1}=w_i+\frac{h}{4}\left(m_1+3 m_3\right)\]

Function file heun.m - nama file harus sama dengan nama fungsi

function [t, w] = heun(f, a, b, N, alpha)
  h = (b - a) / N;
  t = zeros(N + 1, 1);
  w = zeros(N + 1, 1);
  t(1) = a;
  w(1) = alpha;
  for i = 1 : N
    t(i + 1) = t(i) + h;
    m1 = f(t(i), w(i));
    m2 = f(t(i) + (h / 3), w(i) + (h / 3) * m1);
    m3 = f(t(i) + (2 * h / 3), w(i) + (2 * h / 3) * m2);
    w(i + 1) = w(i) + (h / 4) * (m1 + 3 * m3);
  endfor
endfunction

Misalkan diberikan MNA sebagai berikut, yang ingin diselesaikan secara numerik dengan \(N = 10\):

\[y' = y - t^2 + 1\] \[0 \le t \le 2\] \[y(0) = 0.5\]

yang kebetulan memiliki solusi eksak:

\[y\left(t\right) = \left( t + 1 \right)^2 - 0.5 e^t\]

Contoh penggunaan:

Script file coba_heun.m - nama file bebas

f = @(t, y) (y - t .^ 2 + 1);
a = 0;
b = 2;
N = 10;
alpha = 0.5;

[t, w] = heun(f, a, b, N, alpha);

sln = @(t) (t + 1) .^ 2 - 0.5 * exp(t);
y_eksak = sln(t);

err_heun = abs(w - y_eksak);
err_heun_total = sum(err_heun); % norm L1 (taxicab/Manhattan)

disp("Tabel aproksimasi w, solusi y, dan error:");
[t, w, y_eksak, err_heun]
disp("Error total (norm L1):");
disp(err_heun_total);

hold on;
fplot(sln, [a, b], 'b');
scatter(t, w, 'r');
legend("Solusi Eksak", "Metode Heun");

Tabel aproksimasi w, solusi y, dan error:
ans =

        0   0.5000   0.5000        0
   0.2000   0.8292   0.8293   0.0001
   0.4000   1.2140   1.2141   0.0001
   0.6000   1.6488   1.6489   0.0002
   0.8000   2.1270   2.1272   0.0002
   1.0000   2.6406   2.6409   0.0003
   1.2000   3.1796   3.1799   0.0004
   1.4000   3.7320   3.7324   0.0004
   1.6000   4.2830   4.2835   0.0005
   1.8000   4.8147   4.8152   0.0005
   2.0000   5.3050   5.3055   0.0005

Error total (norm L1):
3.0743e-03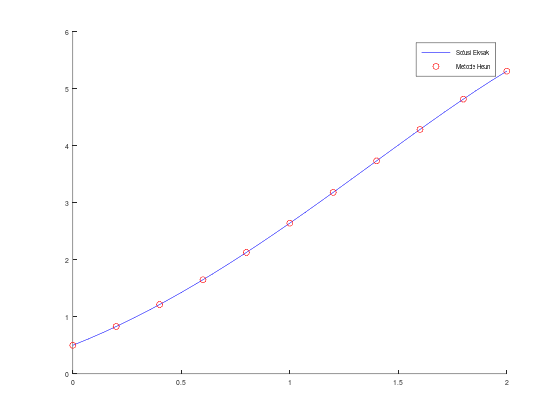

Ternyata errornya sangat kecil! KIta bisa melihat errornya dengan lebih detail/presisi, dengan menggunakan format long

Script file coba2_heun.m - nama file bebas

f = @(t, y) (y - t .^ 2 + 1);
a = 0;
b = 2;
N = 10;
alpha = 0.5;

[t, w] = heun(f, a, b, N, alpha);

sln = @(t) (t + 1) .^ 2 - 0.5 * exp(t);
y_eksak = sln(t);

err_heun = abs(w - y_eksak);
err_heun_total = sum(err_heun); % norm L1 (taxicab/Manhattan)

format long; % pasang format output menjadi panjang (lebih presisi)
disp("Tabel aproksimasi w, solusi y, dan error:");
[t, w, y_eksak, err_heun]
disp("Error total (norm L1):");
disp(err_heun_total);
format; % kembali ke ukuran default

hold on;
fplot(sln, [a, b], 'b');
scatter(t, w, 'r');
legend("Solusi Eksak", "Metode Heun");

Tabel aproksimasi w, solusi y, dan error:
ans =

                   0   0.500000000000000   0.500000000000000                   0
   0.200000000000000   0.829244444444444   0.829298620919915   0.000054176475471
   0.400000000000000   1.213974992592593   1.214087651179365   0.000112658586772
   0.600000000000000   1.648765902064198   1.648940599804746   0.000174697740548
   0.800000000000000   2.126990532832184   2.127229535753766   0.000239002921582
   1.000000000000000   2.640555548543485   2.640859085770478   0.000303537226992
   1.200000000000000   3.179576287732221   3.179941538631727   0.000365250899506
   1.400000000000000   3.731980283861397   3.732400016577663   0.000419732716265
   1.600000000000000   4.283023031133831   4.283483787802441   0.000460756668610
   1.800000000000000   4.814696573135897   4.815176267793527   0.000479694657630
   2.000000000000000   5.305007192434419   5.305471950534676   0.000464758100256

Error total (norm L1):
3.074265993633474e-03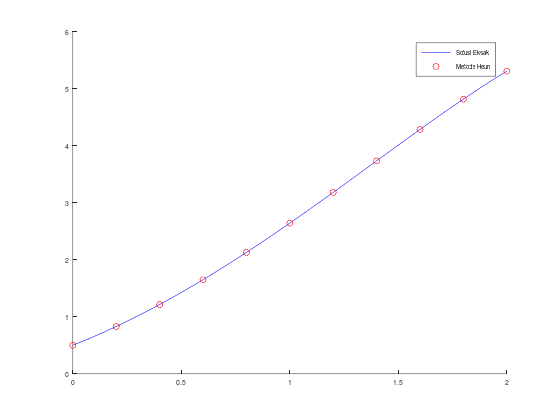

Metode Runge-Kutta orde 4

\[w_1=\alpha\] \[k_1=h f\left(t_i, w_i\right)\] \[k_2=h f\left(t_i+\frac{h}{2}, w_i+\frac{k_1}{2}\right)\] \[k_3=h f\left(t_i+\frac{h}{2}, w_i+\frac{k_2}{2}\right)\] \[k_4=h f\left(t_{i+1}, w_i+k_3\right)\] \[w_{i+1}=w_i+\frac{1}{6}\left(k_1+2 k_2+2 k_3+k_4\right)\]

Function file rko4.m - nama file harus sama dengan nama fungsi

function [t, w] = rko4(f, a, b, N, alpha)
  h = (b - a) / N;
  t = zeros(N + 1, 1);
  w = zeros(N + 1, 1);
  t(1) = a;
  w(1) = alpha;
  for i = 1 : N
    t(i + 1) = t(i) + h;
    k1 = h * f(t(i), w(i));
    k2 = h * f(t(i) + (h / 2), w(i) + (k1 / 2));
    k3 = h * f(t(i) + (h / 2), w(i) + (k2 / 2));
    k4 = h * f(t(i + 1), w(i) + k3);
    w(i + 1) = w(i) + (k1 + 2 * k2 + 2 * k3 + k4) / 6;
  endfor
endfunction

Misalkan diberikan MNA sebagai berikut, yang ingin diselesaikan secara numerik dengan \(N = 10\):

\[y' = y - t^2 + 1\] \[0 \le t \le 2\] \[y(0) = 0.5\]

yang kebetulan memiliki solusi eksak:

\[y\left(t\right) = \left( t + 1 \right)^2 - 0.5 e^t\]

Script file coba_rko4.m - nama file bebas

f = @(t, y) (y - t .^ 2 + 1);
a = 0;
b = 2;
N = 10;
alpha = 0.5;

[t, w] = rko4(f, a, b, N, alpha);

sln = @(t) (t + 1) .^ 2 - 0.5 * exp(t);
y_eksak = sln(t);

err_rko4 = abs(w - y_eksak);
err_rko4_total = sum(err_rko4); % norm L1 (taxicab/Manhattan)

format long; % pasang format output menjadi panjang (lebih presisi)
disp("Tabel aproksimasi w, solusi y, dan error:");
[t, w, y_eksak, err_rko4]
disp("Error total (norm L1):");
disp(err_rko4_total);
format; % kembali ke ukuran default

hold on;
fplot(sln, [a, b], 'b');
scatter(t, w, 'r');
legend("Solusi Eksak", "Metode Runge-Kutta orde 4");

Tabel aproksimasi w, solusi y, dan error:
ans =

                   0   0.500000000000000   0.500000000000000                   0
   0.200000000000000   0.829293333333333   0.829298620919915   0.000005287586582
   0.400000000000000   1.214076210666667   1.214087651179365   0.000011440512698
   0.600000000000000   1.648922017041600   1.648940599804746   0.000018582763146
   0.800000000000000   2.127202684947944   2.127229535753766   0.000026850805823
   1.000000000000000   2.640822692728752   2.640859085770478   0.000036393041726
   1.200000000000000   3.179894170232231   3.179941538631727   0.000047368399497
   1.400000000000000   3.732340072854980   3.732400016577663   0.000059943722683
   1.600000000000000   4.283409498318406   4.283483787802441   0.000074289484035
   1.800000000000000   4.815085694579435   4.815176267793527   0.000090573214092
   2.000000000000000   5.305363000692655   5.305471950534676   0.000108949842021

Error total (norm L1):
4.796793723015336e-04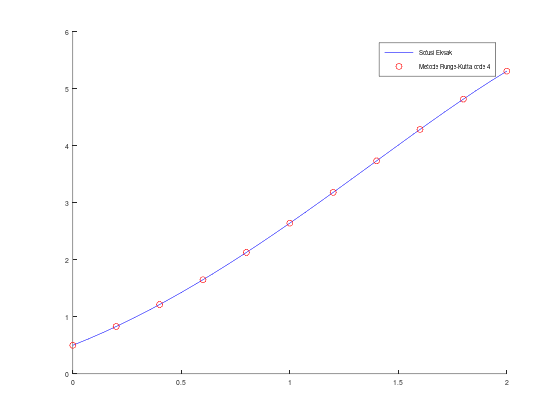

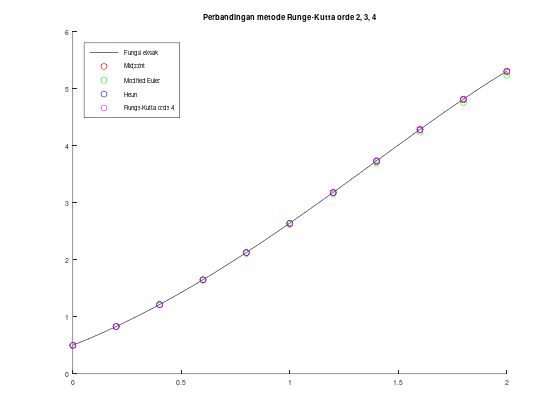
Perbandingan metode Runge-Kutta orde 2, 3, 4

Misalkan diberikan MNA sebagai berikut, yang ingin diselesaikan secara numerik dengan \(N = 10\):

\[y' = y - t^2 + 1\] \[0 \le t \le 2\] \[y(0) = 0.5\]

yang kebetulan memiliki solusi eksak:

\[y\left(t\right) = \left( t + 1 \right)^2 - 0.5 e^t\]

Script file bandingkan_rk234.m - nama file bebas

f = @(t, y) (y - t .^ 2 + 1);
a = 0;
b = 2;
N = 10;
alpha = 0.5;

[t1, w1] = midpoint(f, a, b, N, alpha);
[t2, w2] = modified_euler(f, a, b, N, alpha);
[t3, w3] = heun(f, a, b, N, alpha);
[t4, w4] = rko4(f, a, b, N, alpha);

sln = @(t) (t + 1) .^ 2 - 0.5 * exp(t);
y_eksak = sln(t1);

[t1, w1, w2, w3, w4, y_eksak]

hold on;
fplot(sln, [a, b], 'k');
scatter(t1, w1, 'r');
scatter(t2, w2, 'g');
scatter(t3, w3, 'b');
scatter(t4, w4, 'm');
legend('Fungsi eksak', 'Midpoint', 'Modified Euler', 'Heun', 'Runge-Kutta orde 4');
legend("location", "northwest");
title('Perbandingan metode Runge-Kutta orde 2, 3, 4');

ans =

        0   0.5000   0.5000   0.5000   0.5000   0.5000
   0.2000   0.8280   0.8260   0.8292   0.8293   0.8293
   0.4000   1.2114   1.2069   1.2140   1.2141   1.2141
   0.6000   1.6447   1.6372   1.6488   1.6489   1.6489
   0.8000   2.1213   2.1102   2.1270   2.1272   2.1272
   1.0000   2.6332   2.6177   2.6406   2.6408   2.6409
   1.2000   3.1705   3.1496   3.1796   3.1799   3.1799
   1.4000   3.7212   3.6937   3.7320   3.7323   3.7324
   1.6000   4.2706   4.2351   4.2830   4.2834   4.2835
   1.8000   4.8010   4.7556   4.8147   4.8151   4.8152
   2.0000   5.2904   5.2331   5.3050   5.3054   5.3055