Logistic Regression

Pembelajaran regresi logistic

Offline di Departemen Matematika

Published

November 25, 2024

Struktur Pembelajaran

Halo, selamat sejahtera semua. Kali ini kita akan masuk pembelajaran regresi logistik. Pembelajaran kali ini akan memiliki bertujuan untuk mengetahui secara sederhana untuk kalian dapat menentukan kapan kalian menggunakan regresi linear sederhana & regresi logistik sederhana.

Akan tetapi, bagi kalian yang ingin memahami secara penuh, kita tetap menyediakan penjelasan pada link halaman lainnya.

Mempersiapkan code

Attach Data

Kita akan mendapatkan koleksi data real dari repositori pembelajaran mesin UCI khususnya kita akan mengambil data penyakit jantung

Kita mulai dengan membuat variabel bernama URL dan menyetelnya ke lokasi data yang kita inginkan

url <- "https://raw.githubusercontent.com/StatQuest/logistic_regression_demo/master/processed.cleveland.data"
 
data <- read.csv(url, header=FALSE)

beginilah cara R membaca collection data dari URL.

Fungsi head menunjukkan kepada kita 6 baris data pertama, sayangnya tidak ada kolom yang diberi label

head(data)

  V1 V2 V3  V4  V5 V6 V7  V8 V9 V10 V11 V12 V13 V14
1 63  1  1 145 233  1  2 150  0 2.3   3 0.0 6.0   0
2 67  1  4 160 286  0  2 108  1 1.5   2 3.0 3.0   2
3 67  1  4 120 229  0  2 129  1 2.6   2 2.0 7.0   1
4 37  1  3 130 250  0  0 187  0 3.5   3 0.0 3.0   0
5 41  0  2 130 204  0  2 172  0 1.4   1 0.0 3.0   0
6 56  1  2 120 236  0  0 178  0 0.8   1 0.0 3.0   0

Oh no!

Data nya tidak rapih. Kalau begitu, sekarang …

Pre-Processing Data

Kita menamai kolom tersebut dengan nama yang terdaftar di situs web UCI.

Mari kita format ulang data nya agar:

Mudah digunakan
Ditafsirkan ( interpreted ) dengan benar oleh glm().

colnames(data) <- c(
  "age",
  "sex",# 0 = female, 1 = male
  "cp", # chest pain
  # 1 = typical angina,
  # 2 = atypical angina,
  # 3 = non-anginal pain,
  # 4 = asymptomatic
  "trestbps", # resting blood pressure (in mm Hg)
  "chol", # serum cholestoral in mg/dl
  "fbs",  # fasting blood sugar if less than 120 mg/dl, 1 = TRUE, 0 = FALSE
  "restecg", # resting electrocardiographic results
  # 1 = normal
  # 2 = having ST-T wave abnormality
  # 3 = showing probable or definite left ventricular hypertrophy
  "thalach", # maximum heart rate achieved
  "exang",   # exercise induced angina, 1 = yes, 0 = no
  "oldpeak", # ST depression induced by exercise relative to rest
  "slope", # the slope of the peak exercise ST segment
  # 1 = upsloping
  # 2 = flat
  # 3 = downsloping
  "ca", # number of major vessels (0-3) colored by fluoroscopy
  "thal", # this is short of thalium heart scan
  # 3 = normal (no cold spots)
  # 6 = fixed defect (cold spots during rest and exercise)
  # 7 = reversible defect (when cold spots only appear during exercise)
  "hd" # (the predicted attribute) - diagnosis of heart disease
  # 0 if less than or equal to 50% diameter narrowing
  # 1 if greater than 50% diameter narrowing
)

Hoorayy 🥰 sekarang ketika kita melihat 6 baris pertama dengan fungsi head segalanya terlihat jauh lebih baik🎉

head(data)

  age sex cp trestbps chol fbs restecg thalach exang oldpeak slope  ca thal hd
1  63   1  1      145  233   1       2     150     0     2.3     3 0.0  6.0  0
2  67   1  4      160  286   0       2     108     1     1.5     2 3.0  3.0  2
3  67   1  4      120  229   0       2     129     1     2.6     2 2.0  7.0  1
4  37   1  3      130  250   0       0     187     0     3.5     3 0.0  3.0  0
5  41   0  2      130  204   0       2     172     0     1.4     1 0.0  3.0  0
6  56   1  2      120  236   0       0     178     0     0.8     1 0.0  3.0  0

Namun, fungsi str yang menjelaskan struktur data memberi tahu kita bahwa beberapa kolom sedang kacau saat ini.

str(data) # this shows that we need to tell R which columns contain factors

'data.frame':   303 obs. of  14 variables:
 $ age     : num  63 67 67 37 41 56 62 57 63 53 ...
 $ sex     : num  1 1 1 1 0 1 0 0 1 1 ...
 $ cp      : num  1 4 4 3 2 2 4 4 4 4 ...
 $ trestbps: num  145 160 120 130 130 120 140 120 130 140 ...
 $ chol    : num  233 286 229 250 204 236 268 354 254 203 ...
 $ fbs     : num  1 0 0 0 0 0 0 0 0 1 ...
 $ restecg : num  2 2 2 0 2 0 2 0 2 2 ...
 $ thalach : num  150 108 129 187 172 178 160 163 147 155 ...
 $ exang   : num  0 1 1 0 0 0 0 1 0 1 ...
 $ oldpeak : num  2.3 1.5 2.6 3.5 1.4 0.8 3.6 0.6 1.4 3.1 ...
 $ slope   : num  3 2 2 3 1 1 3 1 2 3 ...
 $ ca      : chr  "0.0" "3.0" "2.0" "0.0" ...
 $ thal    : chr  "6.0" "3.0" "7.0" "3.0" ...
 $ hd      : int  0 2 1 0 0 0 3 0 2 1 ...

# it also shows us that there are some missing values. There are "?"s
# in the dataset. These are in the "ca" and "thal" columns...

kekacauannya adalah sebagai berikut:

sex adalah angka (number) tetapi seharusnya menjadi factor di mana nol mewakili perempuan dan satu mewakili laki laki
CP alias nyeri dada juga seharusnya menjadi factor di mana level 1 hingga 3 mewakili berbagai jenis nyeri dan 4 tidak mewakili nyeri dada
CA dan Thal disebut dengan benar sebagai faktor tetapi salah satu levelnya adalah tanda tanya saat kita membutuhkannya

Jadi kita harus melakukan pembersihan

Cleaning Data

Hal pertama yang kita lakukan adalah

mengubah tanda tanya menjadi NA

## First, convert "?"s to NAs...
data[data == "?"] <- NA

lalu hanya untuk mempermudah melihat data kita mengubah angka nol dalam sex menjadi F untuk perempuan dan yang menjadi M untuk laki laki

## Now add factors for variables that are factors and clean up the factors
## that had missing data...
data[data$sex == 0,]$sex <- "F"
data[data$sex == 1,]$sex <- "M"
data$sex <- as.factor(data$sex)

terakhir kita mengubah kolom yang seharusnya menjadi factor karena memang seharusnya demikian lihat situs web UCI

data$cp <- as.factor(data$cp)
data$fbs <- as.factor(data$fbs)
data$restecg <- as.factor(data$restecg)
data$exang <- as.factor(data$exang)
data$slope <- as.factor(data$slope)

Oh no! Coba perhatikan yang lain sekarang. Karena kolom CA awalnya memiliki tanda tanya di dalamnya alih-alih menganggap itu kolom string, kita mengoreksi asumsi itu dengan memberi tahu bahwa itu adalah kolom integer dan kemudian kita mengubahnya menjadi factor, lalu kita melakukan hal yang sama untuk Thal.

data$ca <- as.integer(data$ca) # since this column had "?"s in it
# R thinks that the levels for the factor are strings, but
# we know they are integers, so first convert the strings to integers...
data$ca <- as.factor(data$ca)  # ...then convert the integers to factor levels

data$thal <- as.integer(data$thal) # "thal" also had "?"s in it.
data$thal <- as.factor(data$thal)

hal lain yang perlu kita lakukan pada data adalah menjadikan HD alias penyakit jantung sebagai factor yang mudah dilihat.

## This next line replaces 0 and 1 with "Healthy" and "Unhealthy"
data$hd <- ifelse(test=data$hd == 0, yes="Healthy", no="Unhealthy")
data$hd <- as.factor(data$hd) # Now convert to a factor

Di sini saya menggunakan trik fancy dengan fungsi if-else untuk mengubah angka nol menjadi sehat dan yang menjadi tidak sehat.

Kita bisa saja melakukan trik serupa untuk sex tapi saya ingin menunjukkan kepada Anda, kedua cara ini untuk mengubah angka menjadi string.

Setelah selesai memperbaiki data, kita periksa bahwa kita telah membuat perubahan yang sesuai kita harapkan dengan fungsi str

str(data) ## this shows that the correct columns are factors

'data.frame':   303 obs. of  14 variables:
 $ age     : num  63 67 67 37 41 56 62 57 63 53 ...
 $ sex     : Factor w/ 2 levels "F","M": 2 2 2 2 1 2 1 1 2 2 ...
 $ cp      : Factor w/ 4 levels "1","2","3","4": 1 4 4 3 2 2 4 4 4 4 ...
 $ trestbps: num  145 160 120 130 130 120 140 120 130 140 ...
 $ chol    : num  233 286 229 250 204 236 268 354 254 203 ...
 $ fbs     : Factor w/ 2 levels "0","1": 2 1 1 1 1 1 1 1 1 2 ...
 $ restecg : Factor w/ 3 levels "0","1","2": 3 3 3 1 3 1 3 1 3 3 ...
 $ thalach : num  150 108 129 187 172 178 160 163 147 155 ...
 $ exang   : Factor w/ 2 levels "0","1": 1 2 2 1 1 1 1 2 1 2 ...
 $ oldpeak : num  2.3 1.5 2.6 3.5 1.4 0.8 3.6 0.6 1.4 3.1 ...
 $ slope   : Factor w/ 3 levels "1","2","3": 3 2 2 3 1 1 3 1 2 3 ...
 $ ca      : Factor w/ 4 levels "0","1","2","3": 1 4 3 1 1 1 3 1 2 1 ...
 $ thal    : Factor w/ 3 levels "3","6","7": 2 1 3 1 1 1 1 1 3 3 ...
 $ hd      : Factor w/ 2 levels "Healthy","Unhealthy": 1 2 2 1 1 1 2 1 2 2 ...

hoooraaayy berhasil 🎉🎉🎉

Handling Missing Value

Sekarang kita melihat berapa banyak baris sampel data yang memiliki nilai na. nanti kita akan memutuskan apakah kita bisa membuang sampel ini atau apakah kita harus memasukkan nilai untuk NA.

## Now determine how many rows have "NA" (aka "Missing data"). If it's just
## a few, we can remove them from the dataset, otherwise we should consider
## imputing the values with a Random Forest or some other imputation method.
nrow(data[is.na(data$ca) | is.na(data$thal),])

[1] 6

data[is.na(data$ca) | is.na(data$thal),]

    age sex cp trestbps chol fbs restecg thalach exang oldpeak slope   ca thal
88   53   F  3      128  216   0       2     115     0     0.0     1    0 <NA>
167  52   M  3      138  223   0       0     169     0     0.0     1 <NA>    3
193  43   M  4      132  247   1       2     143     1     0.1     2 <NA>    7
267  52   M  4      128  204   1       0     156     1     1.0     2    0 <NA>
288  58   M  2      125  220   0       0     144     0     0.4     2 <NA>    7
303  38   M  3      138  175   0       0     173     0     0.0     1 <NA>    3
           hd
88    Healthy
167   Healthy
193 Unhealthy
267 Unhealthy
288   Healthy
303   Healthy

## so 6 of the 303 rows of data have missing values. This isn't a large
## percentage (2%), so we can just remove them from the dataset
nrow(data)

[1] 303

6 baris sampel data memiliki NA di dalamnya.

kita dapat melihat sampel di dalamnya dengan memilih baris tersebut dari dataframe dan di sanalah mereka di sini adalah nilai NA lima dari enam sampel adalah laki-laki dan dua dari enam memiliki penyakit jantung.

data[is.na(data$ca) | is.na(data$thal),]

    age sex cp trestbps chol fbs restecg thalach exang oldpeak slope   ca thal
88   53   F  3      128  216   0       2     115     0     0.0     1    0 <NA>
167  52   M  3      138  223   0       0     169     0     0.0     1 <NA>    3
193  43   M  4      132  247   1       2     143     1     0.1     2 <NA>    7
267  52   M  4      128  204   1       0     156     1     1.0     2    0 <NA>
288  58   M  2      125  220   0       0     144     0     0.4     2 <NA>    7
303  38   M  3      138  175   0       0     173     0     0.0     1 <NA>    3
           hd
88    Healthy
167   Healthy
193 Unhealthy
267 Unhealthy
288   Healthy
303   Healthy

jika kita mau, kita dapat mengaitkan nilai untuk NA menggunakan random forest atau metode lain. namun untuk contoh ini kita hanya akan menghapus sampel ini termasuk enam sampel dalam NA.

nrow(data)

[1] 303

data <- data[!(is.na(data$ca) | is.na(data$thal)),]
nrow(data)

[1] 297

ada tiga ratus tiga sampel kemudian kita menghapus enam sampel yang memiliki NA, dan setelah menghapus sampel tersebut ada dua ratus sembilan puluh tujuh sampel yang tersisa.

Sekarang kita perlu memastikan bahwa sampel yang sehat dan berpenyakit berasal dari setiap jenis kelamin perempuan dan laki-laki.

jika hanya sampel laki-laki yang memiliki penyakit jantung, kita mungkin harus menghapus semua perempuan dari model tersebut.

kita melakukan ini dengan fungsi xtabs kita meneruskan xtabs data dan menggunakan sintaks model untuk memilih kolom dalam data yang ingin kita buat tabelnya. Dalam hal ini kita menginginkan tabel dengan penyakit jantung dan sex.

xtabs(~ hd + sex, data=data)

           sex
hd            F   M
  Healthy    71  89
  Unhealthy  25 112

## Most of the females are healthy and most of the males are unhealthy.
## Being female is likely to decrease the odds in being unhealthy.
##    In other words, if a sample is female, the odds are against it that it
##    will be unhealthy
## Being male is likely to increase the odds in being unhealthy...
##    In other words, if a sample is male, the odds are for it being unhealthy

pasien sehat dan tidak sehat sama-sama diwakili oleh banyak sampel wanita dan pria singkatnya dilaporkan oleh sekelompok pasien.

## Most of the females are healthy and most of the males are unhealthy.
## Being female is likely to decrease the odds in being unhealthy.
##    In other words, if a sample is female, the odds are against it that it
##    will be unhealthy
## Being male is likely to increase the odds in being unhealthy...
##    In other words, if a sample is male, the odds are for it being unhealthy

sekarang mari kita verifikasi bahwa keempat tingkat nyeri dada CP.

## Now we can do some quality control by making sure all of the factor
## levels are represented by people with and without heart disease (hd)
##
## NOTE: We also want to exclude variables that only have 1 or 2 samples in
## a category since +/- one or two samples can have a large effect on the
## odds/log(odds)

xtabs(~ hd + cp, data=data)

           cp
hd            1   2   3   4
  Healthy    16  40  65  39
  Unhealthy   7   9  18 103

Kemudian kita melakukan hal yang sama untuk semua variabel boolean dan categoric yang kita gunakan untuk memprediksi penyakit jantung.

xtabs(~ hd + fbs, data=data)

           fbs
hd            0   1
  Healthy   137  23
  Unhealthy 117  20

xtabs(~ hd + restecg, data=data)

           restecg
hd           0  1  2
  Healthy   92  1 67
  Unhealthy 55  3 79

Inilah sesuatu yang dapat menyebabkan masalah pada hasil istirahat elektrokardiografi. Hanya 4 pasien yang mewakili level 1, hal ini berpotensi menghalangi pencarian jalur yang paling pas (fit). Namun untuk saat ini kita hanya akan membiarkannya dan melihat apa yang terjadi dan kemudian kita terus melihat variabel yang tersisa untuk memastikan bahwa semuanya diwakili oleh sejumlah pasien.

xtabs(~ hd + exang, data=data)

           exang
hd            0   1
  Healthy   137  23
  Unhealthy  63  74

xtabs(~ hd + slope, data=data)

           slope
hd            1   2   3
  Healthy   103  48   9
  Unhealthy  36  89  12

xtabs(~ hd + ca, data=data)

           ca
hd            0   1   2   3
  Healthy   129  21   7   3
  Unhealthy  45  44  31  17

xtabs(~ hd + thal, data=data)

           thal
hd            3   6   7
  Healthy   127   6  27
  Unhealthy  37  12  88

oke kita sudah melakukan semua hal yang membosankan sekarang mari kita lakukan regresi logistik mari kita mulai dengan model yang sangat sederhana.

kita akan mencoba memprediksi penyakit jantung hanya dengan menggunakan jenis kelamin setiap pasien. inilah code call kita ke fungsi GLM fungsi yang menjalankan Generalized Linear Models.

logistic <- glm(hd ~ sex, data=data, family="binomial")

pertama kita menggunakan rumus sintaks untuk menentukan bahwa kita ingin menggunakan jenis kelamin untuk memprediksi penyakit jantung. Kita ingin menggunakan jenis kelamin untuk memprediksi penyakit jantung kemudian kita menentukan data yang kita gunakan untuk model tersebut. Terakhir kita menetapkan bahwa kita menginginkan keluarga binomial dari model linier umum, hal ini membuat fungsi GLM melakukan regresi logistik dibandingkan dengan beberapa jenis model linier umum lainnya.

Oh, saya hampir lupa menyebutkan bahwa kita menyimpan output dari fungsi GLM dalam variabel yang disebut logistic. kita kemudian menggunakan fungsi ringkasan untuk mendapatkan detail tentang regresi logistik.

summary(logistic)


Call:
glm(formula = hd ~ sex, family = "binomial", data = data)

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)  -1.0438     0.2326  -4.488 7.18e-06 ***
sexM          1.2737     0.2725   4.674 2.95e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 409.95  on 296  degrees of freedom
Residual deviance: 386.12  on 295  degrees of freedom
AIC: 390.12

Number of Fisher Scoring iterations: 4

## The intercept is the log(odds) a female will be unhealthy. This is because
## female is the first factor in "sex" (the factors are ordered,
## alphabetically by default,"female", "male")

baris pertama memiliki panggilan asli ke fungsi GLM
baris kedua memberi ringkasan deviance residuals. mereka terlihat bagus karena hampir berpusat pada nol dan kira-kira simetris .

jika Anda ingin tahu lebih banyak tentang deviance residuals, lihat modul deviance residuals yang dijelaskan dengan jelas.

kemudian kita memiliki koefisien. Mereka bersesuaiaian dengan model.

\[ \text{heart disease} = -1.0438 + 1.2737 \times \text{pasien laki-laki} \] Variabel pasien laki-laki sama dengan nol ketika pasien perempuan dan satu ketika pasien laki-laki.

jadi jika kita memprediksi penyakit jantung untuk pasien wanita kita. kita mendapatkan persamaan berikut.

\[ \text{heart disease} = -1.0438 + 1.2737 \times 0 = -1.0438 \] Oleh karena itu, kemungkinan log (odds) bahwa seorang wanita memiliki penyakit jantung $ = -1.0438 $.

jika kita memprediksi penyakit jantung untuk pasien laki-laki, kita mendapatkan persamaan berikut \[ \text{heart disease} = -1.0438 + 1.2737 \times 1 = -1.0438 + 1.2737 \] karena persamaan pertama adalah log(odds) seorang wanita terkena penyakit jantung, persamaan kedua menunjukkan peningkatan log(odds) seorang pria terkena penyakit jantung.

Dengan kata lain, suku persamaan kedua adalah log rasio peluang seorang pria terkena penyakit jantung terhadap kemungkinan seorang wanita terkena penyakit jantung.

female.log.odds <- log(25 / 71)
female.log.odds

[1] -1.043804

female.log.odds <- log(25 / 71)
female.log.odds

[1] -1.043804

## sexM is the log(odds ratio) that tells us that if a sample has sex=M, the
## odds of being unhealthy are, on a log scale, 1.27 times greater than if
## a sample has sex=F.
male.log.odds.ratio <- log((112 / 89) / (25/71))
male.log.odds.ratio

[1] 1.273667

summary(logistic)


Call:
glm(formula = hd ~ sex, family = "binomial", data = data)

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)  -1.0438     0.2326  -4.488 7.18e-06 ***
sexM          1.2737     0.2725   4.674 2.95e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 409.95  on 296  degrees of freedom
Residual deviance: 386.12  on 295  degrees of freedom
AIC: 390.12

Number of Fisher Scoring iterations: 4

Bagian Std. Error dan z Value dari keluaran regresi logistik ini menunjukkan bagaimana Wald dihitung untuk kedua koefisien dan ini adalah P-Value.

kedua P-Value jauh di bawah 0,05 dan dengan demikian log(odds) dan log(odds_ratio) keduanya signifikan secara statistik tetapi ingat P-Value yang kecil saja tidak menentukan.

kita juga menginginkan ukuran efek yang besar dan itulah yang dikatakan oleh log(odds) dan log(odds_ratio).

Jika Anda ingin mengetahui detail lebih lanjut tentang

koefisien dan uji Wald, lihat modul berikut dan
log(odds) dijelaskan dengan jelas - odds_ratio dan
log(odds_ratio) dijelaskan dengan jelas dalam detail regresi logistik bagian 1.

selanjutnya kita melihat parameter dispersi default yang digunakan untuk regresi logistik ini.

Ketika kita melakukan regresi linier sederhana, kita memperkirakan mean dan varians dari data yang berbeda.

Secara kontras, ketika regresi logistik kita memperkirakan rata-rata data sedangkan varians diturunkan dari mean. Karena kita tidak memperkirakan varians dari data dan sebaliknya hanya menurunkannya dari mean ada kemungkinan varians tersebut underestimated. Kalau begitu, Anda dapat menyesuaikan dispersi kita di dalam summary command.

Kita memiliki Null deviance dan Residual Deviance. Ini dapat digunakan untuk membandingkan model yang menghitung $R^2$ dan keseluruhan p-value.

untuk detail lebih lanjut, lihat detail regresi logistik $R^2$ dan p-value-nya dan Saturated Models dan Deviance Statistics dijelaskan dengan jelas.

kemudian kita memiliki AIC (Akaike Information Criterion) yang dalam konteks ini hanyalah Residual Deviance yang disesuaikan dengan jumlah parameter dalam model. AIC dapat digunakan untuk membandingkan satu model dengan model lainnya.
terakhir, kita memiliki Number of Fisher Scoring Iteration yang hanya memberi tahu kita seberapa cepat fungsi GLM coverge pada Maximum Likelihood Estimates untuk koefisien.

jika Anda ingin detail lebih lanjut tentang bagaimana koefisien diestimasi, lihat detail regresi logistik bagian kedua …menyesuaikan garis dengan kemungkinan maksimum.

sekarang kita telah melakukan regresi logistik sederhana hanya dengan menggunakan salah satu variabel (sex) untuk memprediksi penyakit jantung, kita dapat membuat model fancy yang menggunakan semua variabel untuk memprediksi penyakit jantung sintaks dengan rumus ini.

#####################################
##
## Now we will use all of the data available to predict heart disease
##
#####################################
 
logistic <- glm(hd ~ ., data=data, family="binomial")

. berarti kita ingin memodelkan HD penyakit jantung menggunakan semua variabel dalam data frame kita yang disebut data, kita kemudian dapat melihat seperti apa model kita dengan fungsi summary.

summary(logistic)


Call:
glm(formula = hd ~ ., family = "binomial", data = data)

Coefficients:
             Estimate Std. Error z value Pr(>|z|)    
(Intercept) -6.253978   2.960399  -2.113 0.034640 *  
age         -0.023508   0.025122  -0.936 0.349402    
sexM         1.670152   0.552486   3.023 0.002503 ** 
cp2          1.448396   0.809136   1.790 0.073446 .  
cp3          0.393353   0.700338   0.562 0.574347    
cp4          2.373287   0.709094   3.347 0.000817 ***
trestbps     0.027720   0.011748   2.359 0.018300 *  
chol         0.004445   0.004091   1.087 0.277253    
fbs1        -0.574079   0.592539  -0.969 0.332622    
restecg1     1.000887   2.638393   0.379 0.704424    
restecg2     0.486408   0.396327   1.227 0.219713    
thalach     -0.019695   0.011717  -1.681 0.092781 .  
exang1       0.653306   0.447445   1.460 0.144267    
oldpeak      0.390679   0.239173   1.633 0.102373    
slope2       1.302289   0.486197   2.679 0.007395 ** 
slope3       0.606760   0.939324   0.646 0.518309    
ca1          2.237444   0.514770   4.346 1.38e-05 ***
ca2          3.271852   0.785123   4.167 3.08e-05 ***
ca3          2.188715   0.928644   2.357 0.018428 *  
thal6       -0.168439   0.810310  -0.208 0.835331    
thal7        1.433319   0.440567   3.253 0.001141 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 409.95  on 296  degrees of freedom
Residual deviance: 183.10  on 276  degrees of freedom
AIC: 225.1

Number of Fisher Scoring iterations: 6

kita melihat bahwa usia bukanlah prediktor yang berguna karena memiliki p-value yang besar. Namun rata-rata usia dalam dataframe kita adalah $56$ tahun. Jadi sebagian besar orang sudah cukup tua dan itu menjelaskan mengapa usia tidak terlalu berguna.

Gender masih merupakan prediktor yang baik. Meskipun begitu, kita melihat bahwa residual deviance dan AIC keduanya jauh lebih kecil untuk model fancy ini daripada fungsi untuk model sederhana yakni ketika kita hanya menggunakan jenis kelamin untuk memprediksi penyakit jantung.

jika kita ingin menghitung pseudo r-squared McFadden, kita dapat mengambil log-likelihood null model dari variabel logistik, dengan mendapatkan nilai null deviance dan membaginya dengan $-2$,

## Now calculate the overall "Pseudo R-squared" and its p-value
 
## NOTE: Since we are doing logistic regression...
## Null devaince = 2*(0 - LogLikelihood(null model))
##               = -2*LogLikihood(null model)
## Residual deviacne = 2*(0 - LogLikelihood(proposed model))
##                   = -2*LogLikelihood(proposed model)
ll.null <- logistic$null.deviance/-2

dan kita dapat mengambil log-likelihood null model untuk model fancy dari variabel logistik dengan mendapatkan nilai residual deviance dan membaginya dengan $-2$.

## Now calculate the overall "Pseudo R-squared" and its p-value
 
## NOTE: Since we are doing logistic regression...
## Null devaince = 2*(0 - LogLikelihood(null model))
##               = -2*LogLikihood(null model)
## Residual deviacne = 2*(0 - LogLikelihood(proposed model))
##                   = -2*LogLikelihood(proposed model)
ll.proposed <- logistic$deviance/-2

kemudian kita hanya menghitung dan kita mendapatkan pseudo r-squared McFadden $= 0,55$.

## McFadden's Pseudo R^2 = [ LL(Null) - LL(Proposed) ] / LL(Null)
(ll.null - ll.proposed) / ll.null

[1] 0.5533531

ini dapat diartikan sebagai ukuran efek keseluruhan dan kita dapat menggunakan log-likelihood yang sama untuk menghitung p-value untuk $R^2$ tersebut menggunakan distribusi Chi-Square dalam hal ini p-value kecil sehingga nilai $R^2$ bukan karena keberuntungan yang bodoh.

## chi-square value = 2*(LL(Proposed) - LL(Null))
## The p-value for the R^2
1 - pchisq(2*(ll.proposed - ll.null), df=(length(logistic$coefficients)-1))

[1] 0

1 - pchisq((logistic$null.deviance - logistic$deviance), df=(length(logistic$coefficients)-1))

[1] 0

## p-value = 1 - pchisq(chi-square value, df = 2-1)
#1 - pchisq(2*(ll.proposed - ll.null), df=1)
#1 - pchisq((logistic$null.deviance - logistic$deviance), df=1)

## Lastly, let's  see what this logistic regression predicts, given
## that a patient is either female or male (and no other data about them).
predicted.data <- data.frame(
  probability.of.hd=logistic$fitted.values,
  sex=data$sex)

Detail lebih lanjut tentang $R^2$ dan p-value dapat ditemukan di logistic regression details bagian $R^2$ dan p-value.

Terakhir kita dapat menggambar grafik yang menunjukkan probabilitas yang diprediksi bahwa setiap pasien memiliki penyakit jantung seiring dengan status penyakit jantung yang mereka miliki.

## We can plot the data...
ggplot(data=predicted.data, aes(x=sex, y=probability.of.hd)) +
  geom_point(aes(color=sex), size=5) +
  xlab("Sex") +
  ylab("Predicted probability of getting heart disease")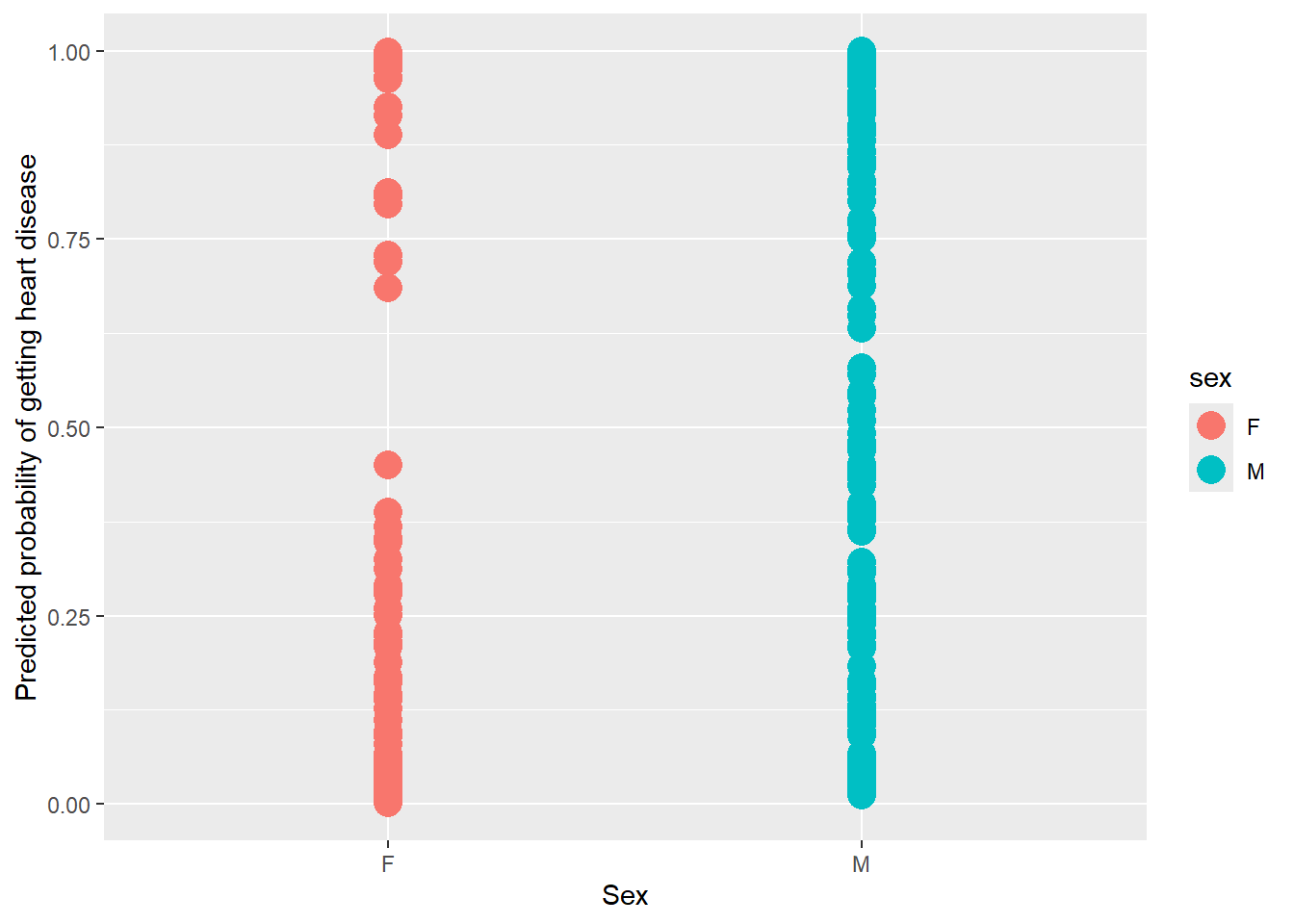

## Since there are only two probabilities (one for females and one for males),
## we can use a table to summarize the predicted probabilities.
xtabs(~ probability.of.hd + sex, data=predicted.data)

                     sex
probability.of.hd     F M
  0.00109849687364516 1 0
  0.00257595371589279 1 0
  0.00302860987165499 1 0
  0.00309742157453941 1 0
  0.00316552701639565 1 0
  0.0036173662362176  1 0
  0.00424728930168456 1 0
  0.004252341397993   1 0
  0.00458417821874386 1 0
  0.0055715691281947  1 0
  0.00612498312810293 1 0
  0.00732920502686092 1 0
  0.00798129825868711 1 0
  0.00821700650426802 1 0
  0.00835492978391896 1 0
  0.0090345742813764  1 0
  0.0102421214716949  1 0
  0.0110000338134468  1 0
  0.0113857038790058  0 1
  0.0119829653935482  1 0
  0.0129839840898876  1 0
  0.0132010374672948  1 0
  0.0141501041600713  0 1
  0.0144510378661266  0 1
  0.0145542087033473  0 1
  0.0150339481250764  1 0
  0.0158412350206649  0 1
  0.0158757921057526  1 0
  0.0163581355975179  0 1
  0.016419911634928   0 1
  0.0167460183841822  0 1
  0.0190015918666313  1 0
  0.0190266058956531  1 0
  0.0194413243424079  1 0
  0.0212397745714133  0 1
  0.0229666682951821  0 1
  0.0234657185428947  0 1
  0.0236604112915081  1 0
  0.0238167919846595  1 0
  0.0249489781010545  1 0
  0.0250971117932175  0 1
  0.0262539988650925  1 0
  0.0285145909079672  1 0
  0.0286625790957844  1 0
  0.0287950230604837  0 1
  0.03037420675039    1 0
  0.0309572735380999  1 0
  0.0311566200786876  0 1
  0.0314432385823954  0 1
  0.0336251680707966  0 1
  0.0355198593538869  0 1
  0.0366238014259639  0 1
  0.0367647167117863  1 0
  0.0386514722522503  0 1
  0.0391214089398116  1 0
  0.0410922083688951  0 1
  0.041439655434854   1 0
  0.0430109609043515  1 0
  0.04367053603076    1 0
  0.0437225372526803  1 0
  0.0440712130839445  1 0
  0.0452121237382874  1 0
  0.0465775926224517  0 1
  0.0490190635751614  0 1
  0.0491266441808808  0 1
  0.0508426014065071  1 0
  0.0508810224168613  1 0
  0.0514768857230768  0 1
  0.052258068609248   0 1
  0.0523329737612425  0 1
  0.0558810524873025  0 1
  0.056834143513995   0 1
  0.0573839959190046  0 1
  0.0583873956994075  0 1
  0.0587245196686592  1 0
  0.0598220299171169  0 1
  0.062099415895352   0 1
  0.0622084822411599  0 1
  0.0644149704119884  0 1
  0.0663940933217283  1 0
  0.0663993133043969  1 0
  0.066924128810457   0 1
  0.0799839139207208  1 0
  0.0896929021776774  1 0
  0.091311778029208   0 1
  0.0924348053526441  1 0
  0.0961869627789141  1 0
  0.096559426661432   0 1
  0.104585965563636   0 1
  0.105461312926022   0 1
  0.110839079905231   0 1
  0.110915898255908   0 1
  0.111011538132575   1 0
  0.113609757343521   0 1
  0.114492942195124   0 1
  0.116842845453753   0 1
  0.124269406166327   0 1
  0.126544057761247   1 0
  0.130489782221405   0 1
  0.138707035572436   1 0
  0.139632265793722   0 1
  0.140838233391067   1 0
  0.142744928155097   1 0
  0.142803306424549   0 1
  0.145321481619698   1 0
  0.154759366190523   0 1
  0.157514867215368   0 1
  0.158988022312673   0 1
  0.160933162511404   1 0
  0.161325645912614   0 1
  0.163686615140895   0 1
  0.16891743464227    1 0
  0.182860431522722   0 1
  0.187798107412366   1 0
  0.207789639077226   0 1
  0.209015413260763   1 0
  0.212072900541564   0 1
  0.214730318385278   1 0
  0.222771394627878   0 1
  0.224006063963778   1 0
  0.227745780140376   1 0
  0.228054267741691   0 1
  0.239284007626666   0 1
  0.241638846352508   0 1
  0.248886621454535   0 1
  0.250309803525568   1 0
  0.254486059487984   0 1
  0.260147992666944   1 0
  0.260211313582116   0 1
  0.270926284230502   0 1
  0.273754102353528   0 1
  0.274486678472416   0 1
  0.277710691706252   0 1
  0.278686451963224   1 0
  0.280420159791897   0 1
  0.28213252291425    1 0
  0.284808944916844   0 1
  0.288415392116847   0 1
  0.290319802806465   1 0
  0.290656356340781   0 1
  0.306943077761505   0 1
  0.311482759100001   0 1
  0.312001019774412   1 0
  0.321379987652644   0 1
  0.324438352928596   1 0
  0.348367591872858   1 0
  0.352439406579044   1 0
  0.361345491709285   0 1
  0.365212639286825   0 1
  0.367992856225714   1 0
  0.368698797256461   1 0
  0.37667186598856    0 1
  0.377552339146292   0 1
  0.381366127903862   0 1
  0.382113408855146   0 1
  0.38673600054482    0 1
  0.38706254718615    1 0
  0.391477771446765   0 1
  0.399258886071222   0 1
  0.422661163229807   0 1
  0.432020604805412   0 1
  0.438010086324275   0 1
  0.445261104770905   0 1
  0.450309481745517   0 1
  0.450534711787278   1 0
  0.451753243490256   0 1
  0.469440882870818   0 1
  0.475457614278839   0 1
  0.47943697237974    0 1
  0.480560386782782   0 1
  0.492615945542668   0 1
  0.509159663847104   0 1
  0.52277745210901    0 1
  0.541141848438452   0 1
  0.544980767718397   0 1
  0.545109373133998   0 1
  0.545390099142261   0 1
  0.546140317975364   0 1
  0.547420365803636   0 1
  0.570442122864816   0 1
  0.578952477298274   0 1
  0.631198562161651   0 1
  0.647739412692096   0 1
  0.658242621846726   0 1
  0.684782513929224   1 0
  0.687452168310232   0 1
  0.70248880783581    0 1
  0.705874158517764   0 1
  0.708644163082159   0 1
  0.717750550408683   0 1
  0.719224535252244   1 0
  0.72005769588199    0 1
  0.728266034396439   1 0
  0.750503476070541   0 1
  0.751145818144816   0 1
  0.754971450824077   0 1
  0.770892650822427   0 1
  0.775235459955928   0 1
  0.796637679798201   1 0
  0.800662839378138   0 1
  0.806879666034612   1 0
  0.811489542804712   1 0
  0.81216422254804    0 1
  0.813179938467691   0 1
  0.813804721189549   0 1
  0.824574972085284   0 1
  0.826936305100827   0 1
  0.845142336159083   0 1
  0.849972280247194   0 1
  0.853137161783436   0 1
  0.856640939423002   0 1
  0.865310778796839   0 1
  0.866587227490961   0 1
  0.880856759614595   0 1
  0.888731337279975   1 0
  0.889990950377614   0 1
  0.894275652973582   0 1
  0.898795127851473   0 1
  0.900556819701189   0 1
  0.913251802637605   1 0
  0.916958660271168   0 1
  0.920857416507447   0 1
  0.922972892897101   0 1
  0.923564289790845   0 1
  0.925103473375611   0 1
  0.92538048837472    1 0
  0.926670249647006   0 1
  0.932562076418011   0 1
  0.940551673245513   0 1
  0.941739080251273   0 1
  0.943991082194031   0 1
  0.954226066930809   0 1
  0.954699941321568   0 1
  0.954869282725921   0 1
  0.957285535359092   0 1
  0.958591574115299   0 1
  0.962311675299815   0 1
  0.962665557808326   1 0
  0.964616179254019   1 0
  0.967083158492448   0 1
  0.972585443725781   0 1
  0.973118236613765   0 1
  0.974849358728931   0 1
  0.974864179016031   1 0
  0.975154296989085   0 1
  0.975923511872864   0 1
  0.976316797250771   0 1
  0.976863952714786   1 0
  0.980524845402496   0 1
  0.981052201584332   0 1
  0.98129752479769    0 1
  0.981593207229319   0 1
  0.981856493751978   0 1
  0.982652584859067   0 1
  0.983817695154674   1 0
  0.984232291394245   1 0
  0.984513939155071   0 1
  0.985418186890805   0 1
  0.986597517143917   0 1
  0.986804485638748   0 1
  0.986878593097864   0 1
  0.987235288448108   0 1
  0.987553136341569   0 1
  0.988237660078016   1 0
  0.988632504331469   0 1
  0.989466670937826   0 1
  0.989498212732539   1 0
  0.990420853263466   0 1
  0.990686567185108   0 1
  0.992386273612647   0 1
  0.993102290185761   0 1
  0.993376136192944   0 1
  0.993471762504122   0 1
  0.993897346285488   0 1
  0.994017714835227   0 1
  0.994109137892823   0 1
  0.994384275170445   0 1
  0.994429272052204   0 1
  0.994568332042835   0 1
  0.994621317393877   0 1
  0.994884640329228   1 0
  0.994921517669052   0 1
  0.995593851495599   0 1
  0.996285859662292   0 1
  0.996938268641653   0 1
  0.997135274510168   0 1
  0.997439675632816   0 1
  0.997935717327889   0 1
  0.99805927561475    0 1
  0.99809095901409    0 1
  0.998313153430203   0 1
  0.998418346757509   1 0
  0.998657002941138   0 1
  0.998862240850775   0 1
  0.998977158173268   0 1
  0.99906284448998    0 1
  0.999172369060652   0 1

Sebagian besar pasien dengan penyakit jantung yang ada di warna Turqoise diprediksi memiliki kemungkinan Tinggi terkena penyakit jantung & Sebagian besar pasien tanpa penyakit jantung yang ada di salmon diprediksi memiliki kemungkinan rendah terkena penyakit jantung sehingga regresi logistik kita telah melakukan pekerjaan yang cukup baik.

Namun, kita dapat menggunakan cross validation untuk mendapatkan ide yang lebih baik tentang seberapa baik kinerjanya dengan data baru. Tetapi kita akan menyimpannya untuk kesempatan lain.

Untuk menggambar grafik kita mulai dengan membuat data frame baru yang berisi probabilitas terkena penyakit jantung bersama dengan status penyakit jantung yang sebenarnya.

## now we can plot the data
predicted.data <- data.frame(
  probability.of.hd=logistic$fitted.values,
  hd=data$hd)

kemudian kita mengurutkan data frame dari probabilitas rendah ke tinggi probabilitas

predicted.data <- predicted.data[
  order(predicted.data$probability.of.hd, decreasing=FALSE),]

kemudian kita tambahkan kolom baru ke data frame yang memiliki rank masing-masing sampel, dari probabilitas rendah ke probabilitas tinggi

predicted.data$rank <- 1:nrow(predicted.data)

kemudian kita memuat library **ggplot2** sehingga kita dapat menggambar grafik yang bagus

library(ggplot2)

kemudian kita memuat library **cowplot** sehingga**ggplot2** memiliki tampilan yang bagus secara defaults

library(cowplot)

kemudian kita memanggil ggplot() dan menggunakan geom_point() untuk menggambar data dan

## Lastly, we can plot the predicted probabilities for each sample having
## heart disease and color by whether or not they actually had heart disease
ggplot(data=predicted.data, aes(x=rank, y=probability.of.hd)) +
  geom_point(aes(color=hd), alpha=1, shape=4, stroke=2) +
  xlab("Index") +
  ylab("Predicted probability of getting heart disease")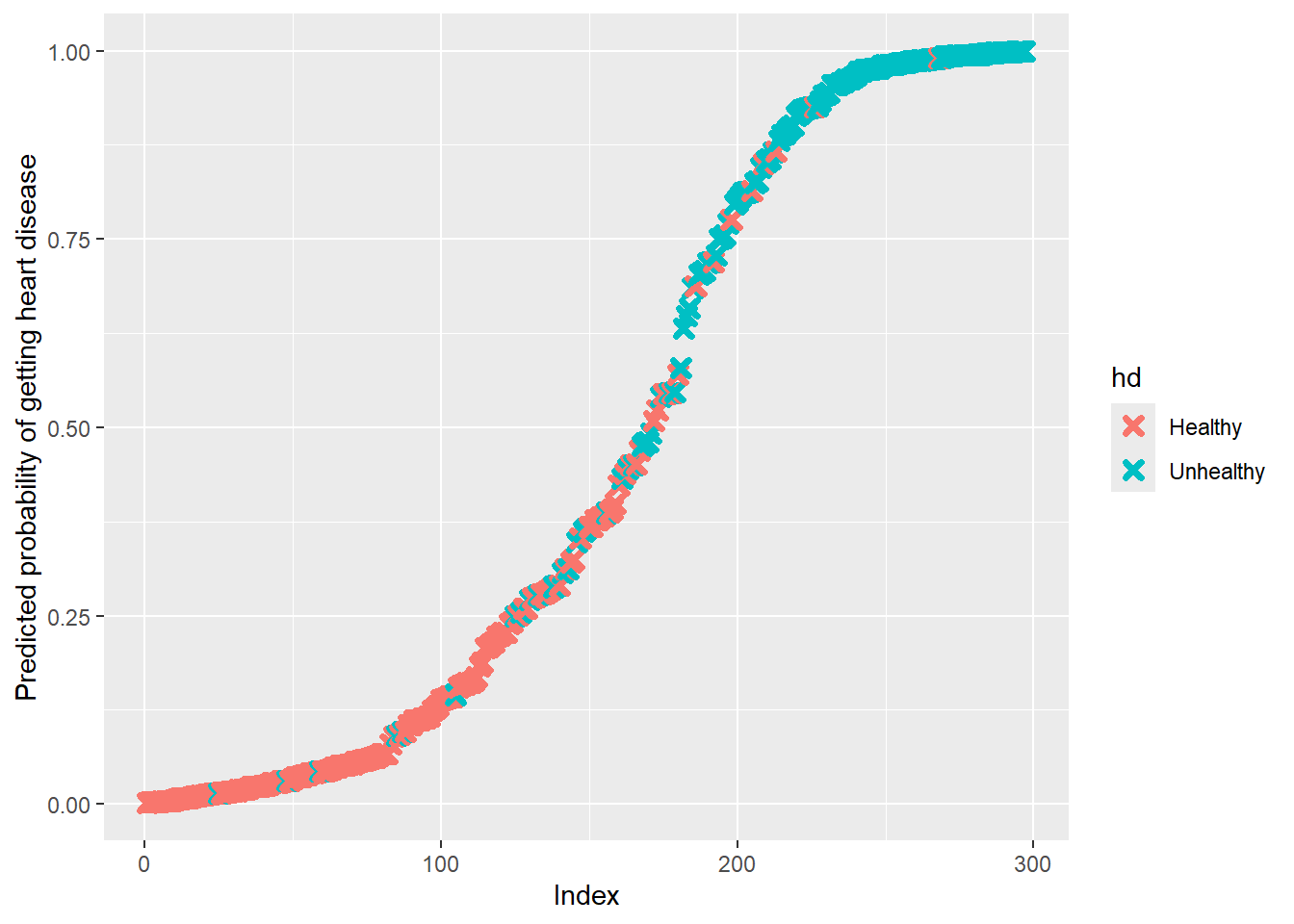

terakhir kita memanggil ggsave() untuk menyimpan grafik sebagai file PDF triple.

ggsave("heart_disease_probabilities.pdf")