Pertemuan 1: Aljabar Matriks di R

Pengantar Multivariat

Offline di Departemen Matematika
Published

September 24, 2024

Notasi Matrix di R

Untuk membuat suatu matrix di R, gunakan fungsi

matrix(<values>, nrow=<jumlah baris>, ncol=<jumlah kolom>, byrow=TRUE/FALSE)

Argumen byrow digunakan untuk mengatur apakah matrix disusun per baris atau per kolom.

A <- matrix(c(1,2,4,1,1,0,1,1,2), nrow=3, ncol=3, byrow=TRUE) # byrow=TRUE -> disusun per baris
A
     [,1] [,2] [,3]
[1,]    1    2    4
[2,]    1    1    0
[3,]    1    1    2
A <- matrix(c(1,2,4,1,1,0,1,1,2), nrow=3, ncol=3, byrow=FALSE) # byrow=FALSE -> disusun per kolom
A
     [,1] [,2] [,3]
[1,]    1    1    1
[2,]    2    1    1
[3,]    4    0    2

Tiap baris dan kolom dapat diberikan nama dengan argumen dimnames=list(rownames, colnames)

# Matriks disusun per baris diberikan nama
rownames = c("row1", "row2", "row3")
colnames = c("col1", "col2", "col3")
A <- matrix(c(1,2,4,1,1,0,1,1,2), nrow=3, ncol=3, byrow=TRUE, dimnames=list(rownames, colnames))
A
     col1 col2 col3
row1    1    2    4
row2    1    1    0
row3    1    1    2

Dataframe to Matrix

Untuk mengubah suat dataframe menjadi matrix, dapat digunakan fungsi as.matrix()

data(iris)
data <- head(iris[, c('Sepal.Length', 'Sepal.Width')])
mat_data <- as.matrix(data)
mat_data
  Sepal.Length Sepal.Width
1          5.1         3.5
2          4.9         3.0
3          4.7         3.2
4          4.6         3.1
5          5.0         3.6
6          5.4         3.9
str(data)
'data.frame':   6 obs. of  2 variables:
 $ Sepal.Length: num  5.1 4.9 4.7 4.6 5 5.4
 $ Sepal.Width : num  3.5 3 3.2 3.1 3.6 3.9
str(mat_data)
 num [1:6, 1:2] 5.1 4.9 4.7 4.6 5 5.4 3.5 3 3.2 3.1 ...
 - attr(*, "dimnames")=List of 2
  ..$ : chr [1:6] "1" "2" "3" "4" ...
  ..$ : chr [1:2] "Sepal.Length" "Sepal.Width"

Operasi Matrix

Penjumlahan dan Pengurangan

Operasi penjumlahan dan pengurangan pada matriks dapat dilakukan layaknya operasi penjumlahan dan pengurangan pada skalar di R

A <- matrix(c(1,1,2,3,1,1,4,1,3), ncol=3, byrow=T)
B <- matrix(c(1,2,3,1,1,4,5,6,7), ncol=3, byrow=T)
A
     [,1] [,2] [,3]
[1,]    1    1    2
[2,]    3    1    1
[3,]    4    1    3
B
     [,1] [,2] [,3]
[1,]    1    2    3
[2,]    1    1    4
[3,]    5    6    7
A + B
     [,1] [,2] [,3]
[1,]    2    3    5
[2,]    4    2    5
[3,]    9    7   10
A - B
     [,1] [,2] [,3]
[1,]    0   -1   -1
[2,]    2    0   -3
[3,]   -1   -5   -4

Perkalian Matriks dengan Skalar

Operasi perkalian pada matriks dapat dilakukan layaknya operasi perkalian pada skalar di R

A <- matrix(c(1,1,3,2,1,4), ncol=3, byrow=T)
k <- 2

k * A
     [,1] [,2] [,3]
[1,]    2    2    6
[2,]    4    2    8

Perkalian Matriks dengan Matriks

Operasi perkalian matriks dengan matriks harus menggunakan tanda %*%

A <- matrix(c(1,1,1,1,2,1), ncol=3, byrow=T)
B <- matrix(c(2,1,1,2,3,1), nrow=3, byrow=T)
A
     [,1] [,2] [,3]
[1,]    1    1    1
[2,]    1    2    1
B
     [,1] [,2]
[1,]    2    1
[2,]    1    2
[3,]    3    1
A %*% B
     [,1] [,2]
[1,]    6    4
[2,]    7    6
Hadamard Product (Element-wise Multiplication)

Melakukan perkalian matriks dengan matriks tanpa menggunakan tanda % akan melakukan operator lain, yaitu Hadamard Product

A <- matrix(c(2,0,-1,4,1,3), ncol=3, byrow=T)
B <- matrix(c(1,3,7,2,0,6), ncol=3, byrow=T)
A
     [,1] [,2] [,3]
[1,]    2    0   -1
[2,]    4    1    3
B
     [,1] [,2] [,3]
[1,]    1    3    7
[2,]    2    0    6
A * B
     [,1] [,2] [,3]
[1,]    2    0   -7
[2,]    8    0   18

Transpose

Transpose matriks dapat dilakukan dengan fungsi t()

A <- matrix(c(1,1,3,5,2,1,1,0,1,2,3,5), ncol=4, byrow=T)
A
     [,1] [,2] [,3] [,4]
[1,]    1    1    3    5
[2,]    2    1    1    0
[3,]    1    2    3    5
t(A)
     [,1] [,2] [,3]
[1,]    1    2    1
[2,]    1    1    2
[3,]    3    1    3
[4,]    5    0    5

Trace

Untuk penghitungan trace, diperlukan library matlib dengan fungsi tr()

library(matlib)
A <- matrix(c(1,7,6,8,3,9,4,-2,-8), ncol=3, byrow=T)
A
     [,1] [,2] [,3]
[1,]    1    7    6
[2,]    8    3    9
[3,]    4   -2   -8
tr(A) # 1 + 3 - 8 = -4
[1] -4

Determinan

Determinan matriks dapat dihitung dengan fungsi det()

A <- matrix(c(1,3,2,8,17,21,2,7,1), ncol=3, byrow=T)
A
     [,1] [,2] [,3]
[1,]    1    3    2
[2,]    8   17   21
[3,]    2    7    1
det(A)
[1] 16

Invers

Invers matriks A dapat dihitung dengan fungsi solve(A)

A <- matrix(c(1,3,2,8,17,21,2,7,1), ncol=3, byrow=T)
A
     [,1] [,2] [,3]
[1,]    1    3    2
[2,]    8   17   21
[3,]    2    7    1
solve(A)
       [,1]    [,2]    [,3]
[1,] -8.125  0.6875  1.8125
[2,]  2.125 -0.1875 -0.3125
[3,]  1.375 -0.0625 -0.4375

Power Matrix

Matriks A^n dapat dihitung dengan operator A %^% n

library(expm)
n <- 3
A <- matrix(c(1,1,2,3,1,1,4,1,3), ncol=3, byrow=T)
A
     [,1] [,2] [,3]
[1,]    1    1    2
[2,]    3    1    1
[3,]    4    1    3
A %^% n
     [,1] [,2] [,3]
[1,]   60   25   55
[2,]   65   25   55
[3,]  115   45  100
Batasan n pada A %^% n Power Matrix

Power matrix dalam fungsi dari library expm ini mengasumsikan nilai n adalah bilangan bulat positif. Jika ingin menggunakan nilai n non bilangan bulat positif.

Square Root Matrix

Dari library expm, dapat dicari akar kuadrat dari suatu matrix dengan fungsi sqrtm

sqrtm(A)
                     [,1]                 [,2]                 [,3]
[1,] 0.7996281+0.7653010i 0.3420350-0.1942727i 0.6718684-0.3063164i
[2,] 1.0505083-0.7472764i 0.8850394+0.1896972i 0.2688254+0.2991019i
[3,] 1.3315353-0.5304036i 0.2932286+0.1346437i 1.5081014+0.2122973i

Bukti:

round(Re(sqrtm(A) %*% sqrtm(A)))
     [,1] [,2] [,3]
[1,]    1    1    2
[2,]    3    1    1
[3,]    4    1    3

Matriks Identitas

Matriks identitas n x n dapat dengan mudah dibuat menggunakan fungsi diag(n)

diag_mat <- diag(5)
diag_mat
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    0    0    0    0
[2,]    0    1    0    0    0
[3,]    0    0    1    0    0
[4,]    0    0    0    1    0
[5,]    0    0    0    0    1

Vektor

Notasi vektor sama dengan membuat suatu matriks dengan ncol=1

x <- matrix(c(1,0,2), ncol=1, byrow=T)
y <- matrix(c(2,2,1), ncol=1, byrow=T)
x
     [,1]
[1,]    1
[2,]    0
[3,]    2
y
     [,1]
[1,]    2
[2,]    2
[3,]    1

Inner Product

print(t(x) %*% y) # bentuk skalar dan simetri
     [,1]
[1,]    4

Outer Product

print(x %*% t(y)) # tidak bersifat simetri
     [,1] [,2] [,3]
[1,]    2    2    1
[2,]    0    0    0
[3,]    4    4    2

Rank Matriks

Untuk menghitung rank matriks, dibutuhkan library Matrix dengan fungsi rankMatrix()

library(Matrix)
A <- matrix(c(5,-14,2,-10,-5,-10,10,2,-4), ncol=3, byrow=T)
rankMatrix(A)
[1] 3
attr(,"method")
[1] "tolNorm2"
attr(,"useGrad")
[1] FALSE
attr(,"tol")
[1] 6.661338e-16

Bentuk Eselon Baris

Untuk membuat bentuk eselon baris suatu matriks, dibutuhkan library matlib dengan fungsi echelon()

A <- matrix(c(-1,2,0,4,5,-3,3,-7,2,0,1,4,2,-5,2,4,6,1,4,-9,2,-4,-4,7), ncol=6, byrow=T)
echelon(A, reduced = TRUE)
     [,1] [,2] [,3] [,4] [,5] [,6]
[1,]    1    0   -4  -28  -37   13
[2,]    0    1   -2  -12  -16    5
[3,]    0    0    0    0    0    0
[4,]    0    0    0    0    0    0

Eigenvalues

Untuk mencari nilai eigen, gunakan fungsi eigen() dan akses nilainya dengan $values

A <- matrix(c(4,2,2,2,4,2,2,2,4), ncol=3, byrow = TRUE)
A
     [,1] [,2] [,3]
[1,]    4    2    2
[2,]    2    4    2
[3,]    2    2    4
eig_val <- eigen(A)$values
eig_val
[1] 8 2 2

Eigenvectors

Untuk mencari vektor eigen dari nilai eigen yang bersesuaian, gunakan $vectors

eig_vec <- eigen(A)$vectors * (-1) # Dikalikan dengan -1
eig_vec
          [,1]       [,2]       [,3]
[1,] 0.5773503  0.0000000 -0.8164966
[2,] 0.5773503  0.7071068  0.4082483
[3,] 0.5773503 -0.7071068  0.4082483

Dekomposisi Spectral

Dari eigenvalues dan eigenvector, dapat dibentuk suatu dekomposisi spektral dari suatu matriks.

round(eig_vec %*% diag(eig_val) %*% t(eig_vec))
     [,1] [,2] [,3]
[1,]    4    2    2
[2,]    2    4    2
[3,]    2    2    4

Dekomposisi Cholesky

Dekomposisi cholesky dari suatu matriks A dapat dilakukan dengan fungsi chol(A)

A <- matrix(c(3,0,-3,0,6,3,-3,3,6), ncol=3, byrow=T)
A
     [,1] [,2] [,3]
[1,]    3    0   -3
[2,]    0    6    3
[3,]   -3    3    6
chol(A)
         [,1]    [,2]      [,3]
[1,] 1.732051 0.00000 -1.732051
[2,] 0.000000 2.44949  1.224745
[3,] 0.000000 0.00000  1.224745

Sehingga dapat dibuktikan A = U`U dengan U matriks segitiga atas dari dekomposisi cholesky matriks A

t(chol(A)) %*% chol(A)
     [,1] [,2] [,3]
[1,]    3    0   -3
[2,]    0    6    3
[3,]   -3    3    6

Singular Value Decomposition (SVD)

A <- matrix(c(1,0,1,0,1,0), ncol=3, byrow = TRUE)
A
     [,1] [,2] [,3]
[1,]    1    0    1
[2,]    0    1    0
svd_A <- svd(A)

Nilai diagonal matriks D dapat diakses dengan $d

svd_A$d
[1] 1.414214 1.000000

Matriks U dapat diakses dengan $u

svd_A$u
     [,1] [,2]
[1,]    1    0
[2,]    0    1

Matriks V dapat diakses dengan $v

svd_A$v
          [,1] [,2]
[1,] 0.7071068    0
[2,] 0.0000000    1
[3,] 0.7071068    0

Sehingga dapat dibuktikan A = UDV`

svd_A$u %*% diag(svd_A$d) %*% t(svd_A$v)
     [,1] [,2] [,3]
[1,]    1    0    1
[2,]    0    1    0

Ortogonalisasi Matrix (Gram-Schmidt)

Ortogonalisasi matrix dengan proses Gram-Schmidt dapat dilakukan dengan fungsi GramSchmidt() dari library matlib.

A <- matrix(c( 1:3, 3:1, 1, 0, -2), 3, 3)
A
     [,1] [,2] [,3]
[1,]    1    3    1
[2,]    2    2    0
[3,]    3    1   -2
GramSchmidt(A)
          [,1]       [,2]       [,3]
[1,] 0.2672612  0.8728716 -0.4082483
[2,] 0.5345225  0.2182179  0.8164966
[3,] 0.8017837 -0.4364358 -0.4082483

Bukti:

A_gs <- GramSchmidt(A)
round(A_gs %*% t(A_gs))
     [,1] [,2] [,3]
[1,]    1    0    0
[2,]    0    1    0
[3,]    0    0    1

Latihan Soal

Diberikan matriks berikut

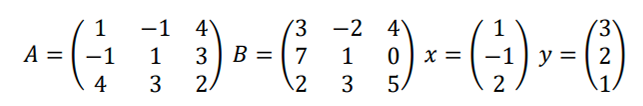
Carilah nilai:

  1. 2.576 x (A + B)

  2. Bx

  3. y`B

  4. x`Ay

  5. Inner product dari x dan x

  6. Inner product dari x dan y

  7. Outer product dari y dan y

  8. Nilai eigen dari A menggunakan eigen()$values dan hitung tanpa bantuan kode. Apakah nilainya sama?

  9. Vektor eigen dari A menggunakan fungsi eigen()$vectors dan hitung tanpa bantuan kode. Apakah nilainya sama?

  10. Matriks U, D dan V dari singular value decomposition pada invers dari matriks B