Pertemuan 3: Karakteristik Data Multivariat

Pengantar Multivariat

Offline di Departemen Matematika
Published

October 28, 2024

Pada pertemuan kali ini, kita akan menggunakan data dari tabel 3.7 (Ramus Bone) dari buku Methods of Multivariate Analysis by Alvin C. Rencher, William F. Christensen. 3rd Edition

data <- read.csv('https://raw.githubusercontent.com/farhanage/dataset-for-study/refs/heads/main/Analisis%20Multivariat/Tabel%203.7%20(Ramus%20Bone%20Length%20at%20Four%20Ages%20).csv', sep=';')

head(data)
  Individual   y1   y2   y3   y4
1          1 47.8 48.8 49.0 49.7
2          2 46.4 47.3 47.7 48.4
3          3 46.3 46.8 47.8 48.5
4          4 45.1 45.3 46.1 47.2
5          5 47.6 48.5 48.9 49.3
6          6 52.5 53.2 53.3 53.7

definisikan matriks Y

Y <- as.matrix(data[2:5])
Y
        y1   y2   y3   y4
 [1,] 47.8 48.8 49.0 49.7
 [2,] 46.4 47.3 47.7 48.4
 [3,] 46.3 46.8 47.8 48.5
 [4,] 45.1 45.3 46.1 47.2
 [5,] 47.6 48.5 48.9 49.3
 [6,] 52.5 53.2 53.3 53.7
 [7,] 51.2 53.0 54.3 54.5
 [8,] 49.8 50.0 50.3 52.7
 [9,] 48.1 50.8 52.3 54.4
[10,] 45.0 47.0 47.3 48.3
[11,] 51.2 51.4 51.6 51.9
[12,] 48.5 49.2 53.0 55.5
[13,] 52.1 52.8 53.7 55.0
[14,] 48.2 48.9 49.3 49.8
[15,] 49.6 50.4 51.2 51.8
[16,] 50.7 51.7 52.7 53.3
[17,] 47.2 47.7 48.4 49.5
[18,] 53.3 54.6 55.1 55.3
[19,] 46.2 47.5 48.1 48.4
[20,] 46.3 47.6 51.3 51.8

Vektor Mean

Vektor mean dari matriks Y dapat dihitung dengan fungsi colMeans()

colMeans(Y)
    y1     y2     y3     y4 
48.655 49.625 50.570 51.450

Matriks Varians-Kovarians

Matriks varians-kovarians dari matriks Y dapat dihitung dengan fungsi cov()

cov(Y)
         y1       y2       y3       y4
y1 6.329974 6.189079 5.777000 5.548158
y2 6.189079 6.449342 6.153421 5.923421
y3 5.777000 6.153421 6.918000 6.946316
y4 5.548158 5.923421 6.946316 7.464737

Generalized Sample Variance

Generalized Sample Variance dari matriks Y dapat dihitung dengan mencari determinan dari matriks varians-kovarians Y

cov_Y <- cov(Y)
det(cov_Y)
[1] 1.068328

Total Sample Variance

Total Sample Variance dari matriks Y dapat dihitung dengan mencari trace dari matriks varians-kovarians Y

library(matlib)
Warning: package 'matlib' was built under R version 4.4.1
tr(cov_Y)
[1] 27.16205

Matriks Korelasi

Matriks Korelasi dari matriks Y dapat dihitung dengan fungsi cor()

cor(Y)
          y1        y2        y3        y4
y1 1.0000000 0.9686511 0.8729938 0.8071246
y2 0.9686511 1.0000000 0.9212312 0.8537046
y3 0.8729938 0.9212312 1.0000000 0.9666227
y4 0.8071246 0.8537046 0.9666227 1.0000000

Matriks dengan Subset Variabel

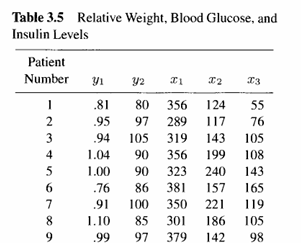
Tinjau data dari tabel 3.5 buku rencher (Relative Weight, Blood Glucose, and Insulin Levels)

T3_5 <- read.table('https://raw.githubusercontent.com/farhanage/dataset-for-study/refs/heads/main/Analisis%20Multivariat/T3_5_DIABETES.DAT')
head(T3_5)
  V1   V2  V3  V4  V5  V6
1  1 0.81  80 356 124  55
2  2 0.95  97 289 117  76
3  3 0.94 105 319 143 105
4  4 1.04  90 356 199 108
5  5 1.00  90 323 240 143
6  6 0.76  86 381 157 165

definisikan bentuk matriksnya

M3_5 <- as.matrix(T3_5[2:6])
colnames(M3_5) <- c('y1', 'y2', 'x1', 'x2', 'x3')
head(M3_5)
       y1  y2  x1  x2  x3
[1,] 0.81  80 356 124  55
[2,] 0.95  97 289 117  76
[3,] 0.94 105 319 143 105
[4,] 1.04  90 356 199 108
[5,] 1.00  90 323 240 143
[6,] 0.76  86 381 157 165

Vektor Mean Subset

Sama seperti pada vektor mean sebelumnya, dapat digunakan fungsi colMeans()

mean_vec <- colMeans(M3_5)
mean_vec
         y1          y2          x1          x2          x3 
  0.9178261  90.4130435 340.8260870 171.3695652  97.7826087 
y_bar <- mean_vec[1:2]; y_bar
        y1         y2 
 0.9178261 90.4130435 
x_bar <- mean_vec[3:5]; x_bar
       x1        x2        x3 
340.82609 171.36957  97.78261

Matriks Varians-Kovarians Subset

Sama seperti pada Matriks Varians-Kovarians sebelumnya, dapat digunakan fungsi cov()

S <- cov(M3_5)
S
            y1         y2           x1           x2          x3
y1  0.01618184   0.216029    0.7871691   -0.2138454    2.189072
y2  0.21602899  70.558937   26.2289855  -23.9560386  -20.841546
x1  0.78716908  26.228986 1106.4135266  396.7323671  108.383575
x2 -0.21384541 -23.956039  396.7323671 2381.8826087 1142.637681
x3  2.18907246 -20.841546  108.3835749 1142.6376812 2136.396135

Partisi Matriks Varians-Kovarians

Partisi dari matriks (subset) dapat diakses deangan indexing baris dan kolom suatu matriks.

Indexing pada matrix di R

Indexing pada matrix dapat dilakukan dengan format matrix_obj[<rangebaris>, <rangekolom>]

misal ingin diambil nilai baris ke 1 hingga 2 dan kolom 3 hingga 4 dari matriks Y, maka dapat dilakukan indexing:

Y[1:2, 3:4]

S_xx <- S[1:2, 1:2]; S_xx
           y1        y2
y1 0.01618184  0.216029
y2 0.21602899 70.558937
S_yy <- S[3:5, 3:5]; S_yy
          x1        x2        x3
x1 1106.4135  396.7324  108.3836
x2  396.7324 2381.8826 1142.6377
x3  108.3836 1142.6377 2136.3961
S_xy <- S[3:5, 1:2]; S_xy
           y1        y2
x1  0.7871691  26.22899
x2 -0.2138454 -23.95604
x3  2.1890725 -20.84155
S_yx <- S[1:2, 3:5]; S_yx
           x1          x2         x3
y1  0.7871691  -0.2138454   2.189072
y2 26.2289855 -23.9560386 -20.841546

Matriks Korelasi Subset

Sama seperti pada Matriks Korelasi sebelumnya, dapat digunakan fungsi cor()

R <- cor(M3_5)
R
            y1          y2         x1          x2          x3
y1  1.00000000  0.20217252 0.18603532 -0.03444497  0.37231056
y2  0.20217252  1.00000000 0.09387431 -0.05843578 -0.05368006
x1  0.18603532  0.09387431 1.00000000  0.24438735  0.07049590
x2 -0.03444497 -0.05843578 0.24438735  1.00000000  0.50653268
x3  0.37231056 -0.05368006 0.07049590  0.50653268  1.00000000

Partisi korelasi dapat dilakukan sebagaimana partisi dilakukan pada matriks Varians-Kovarians Subset

Kombinasi Linear Vektor

misal ingin dibentuk:

\(z_1 = y_1 + y_2 + y_3 + y_4\)

dan

\(z_2 = 2y_1 + 3y_2 - 4y_3 - y_4\)

# z1 = y1 + y2 + y3 + y4
z1 <- Y[, 1] + Y[, 2] + Y[, 3] + Y[, 4]
z1
 [1] 195.3 189.8 189.4 183.7 194.3 212.7 213.0 202.8 205.6 187.6 206.1 206.2
[13] 213.6 196.2 203.0 208.4 192.8 218.3 190.2 197.0
# z2 = 2y1 + 3y2 - 4y3 - y4
z2 <- 2*Y[, 1] + 3*Y[, 2] - 4*Y[, 3] - Y[, 4]
z2
 [1]  -3.7  -4.5  -6.7  -5.5  -4.2  -2.3 -10.3  -4.3 -15.0  -6.5  -1.7 -22.9
[13]  -7.2  -3.9  -6.2  -7.6  -5.6  -5.3  -5.9 -21.6
Y
        y1   y2   y3   y4
 [1,] 47.8 48.8 49.0 49.7
 [2,] 46.4 47.3 47.7 48.4
 [3,] 46.3 46.8 47.8 48.5
 [4,] 45.1 45.3 46.1 47.2
 [5,] 47.6 48.5 48.9 49.3
 [6,] 52.5 53.2 53.3 53.7
 [7,] 51.2 53.0 54.3 54.5
 [8,] 49.8 50.0 50.3 52.7
 [9,] 48.1 50.8 52.3 54.4
[10,] 45.0 47.0 47.3 48.3
[11,] 51.2 51.4 51.6 51.9
[12,] 48.5 49.2 53.0 55.5
[13,] 52.1 52.8 53.7 55.0
[14,] 48.2 48.9 49.3 49.8
[15,] 49.6 50.4 51.2 51.8
[16,] 50.7 51.7 52.7 53.3
[17,] 47.2 47.7 48.4 49.5
[18,] 53.3 54.6 55.1 55.3
[19,] 46.2 47.5 48.1 48.4
[20,] 46.3 47.6 51.3 51.8

Latihan Soal

Gunakan data dari tabel 3.5 buku rencher untuk mengerjakan soal-soal berikut:

  1. bentuk matrix \(Z = (z_1, z_2, z_3)\) dengan

\(z_1 = x_1 + x_2 + x_3\)

\(z_2 = 3y_1 + 2y_2 - x_1^{0.5} - 3x_2 + 7x_3\)

dan

\(z_3 = y_1^2 + y_2 - 5x_1 + 2x_2 - x_3\)

  1. Tentukan Vektor Mean dari matriks Z

  2. Tentukan Matriks Varians-Kovarians dari matriks Z

  3. Tentukan Nilai Generalized Sample Variance dari matriks Z

  4. Tentukan Matriks Korelasi dari matriks Z