Pertemuan 5: Uji Beda Mean Data Multivariat

Pengantar Multivariat

Offline di Departemen Matematika
Published

November 12, 2024

Review Uji Beda Mean 1 Sampel Univariat

Dalam uji beda mean 1 sampel univariat, hipotesis yang ingin kita uji adalah

\(H_0: \mu = \mu_0\)
\(H_1: \mu \neq \mu_0\)

dengan \(\mu_0\) adalah nilai mean yang ditentukan.

Ketika Variansi Diketahui

Asumsi n observasi sampel acak \(y_1, y_2, ..., y_n\) berdistribusi \(N(\mu,\sigma^2)\) dengan \(\sigma^2\) diketahui, maka digunakan statistik uji \(z\) yaitu

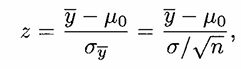
Tolak \(H_0\) pada taraf signifikansi \(\alpha\) jika \(|z| \geq z_{\alpha/2}\)

Atau dengan distribusi chi-square

Tolak \(H_0\) pada taraf signifikansi \(\alpha\) jika \(z^2 \geq \chi^2_{\alpha, 1}\)

Implementasi Program

Uji \(z\) dapat dilakukan dengan memanggil fungsi z.test() pada r dari library BSDA

library(BSDA)
data <- c(88, 92, 94, 94, 96, 97, 97, 97, 99, 99, 105, 109, 109, 109, 110, 112, 112, 113, 114, 115)
z.test(data, mu = 100, sigma.x = 15)

    One-sample z-Test

data:  data
z = 0.90933, p-value = 0.3632
alternative hypothesis: true mean is not equal to 100
95 percent confidence interval:
  96.47608 109.62392
sample estimates:
mean of x 
   103.05

Ketika Variansi Tidak Diketahui

Ketika variansi tidak diketahui, gunakan estimasi sampel dari \(\sigma^2\) yaitu \(s^2\), di mana

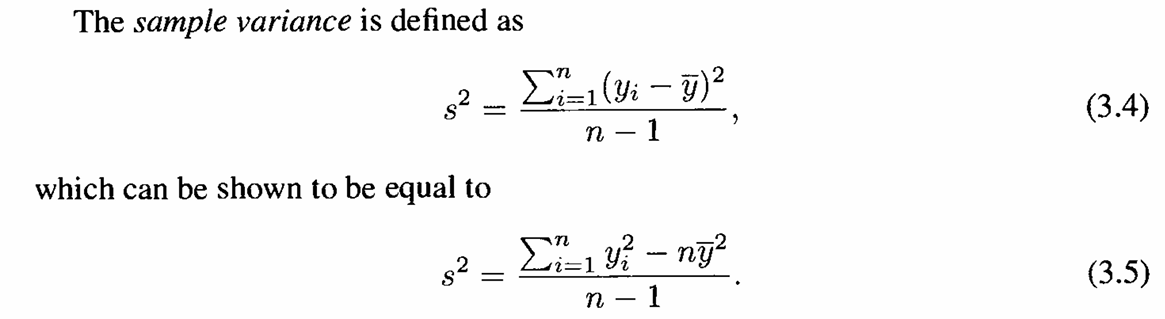
Uji yang digunakan adalah uji \(t\), dengan statistik uji:

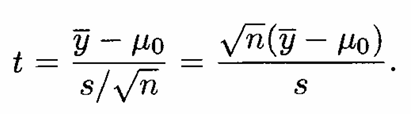
Tolak \(H_0\) pada taraf signifikansi \(\alpha\) jika \(|t| \geq t_{\alpha/2, n-1}\)

Implementasi Program

data <- c(88, 92, 94, 94, 96, 97, 97, 97, 99, 99, 105, 109, 109, 109, 110, 112, 112, 113, 114, 115)

t.test(data, mu=100)

    One Sample t-test

data:  data
t = 1.5976, df = 19, p-value = 0.1266
alternative hypothesis: true mean is not equal to 100
95 percent confidence interval:
  99.05424 107.04576
sample estimates:
mean of x 
   103.05

Uji Beda Mean 1 Sampel Multivariat

Dalam uji beda mean 1 sampel multivariat, hipotesis yang ingin kita uji adalah

\(H_0: \pmb{\mu} = \pmb{\mu_0}\)
\(H_1: \pmb{\mu} \neq \pmb{\mu_0}\)

dengan \(\pmb{\mu_0}\) adalah vektor mean yang ditentukan.

Ketika Variansi Diketahui

Asumsi n vektor observasi sampel acak \(\pmb{y}_1, \pmb{y}_2, ..., \pmb{y}_n\) berdistribusi \(N_p(\pmb{\mu},\pmb{\Sigma})\) dengan \(\pmb{\Sigma}\) diketahui, maka digunakan statistik uji \(Z^2\) yaitu

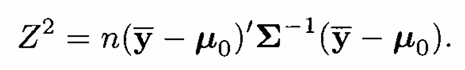
Tolak \(H_0\) pada taraf signifikansi \(\alpha\) jika \(Z^2 > \chi^2_{\alpha, p}\)

Implementasi Program

Digunakan data dari tabel 3.7 (Ramus Bone) dari buku Methods of Multivariate Analysis by Alvin C. Rencher, William F. Christensen. 3rd Edition

Misalkan ingin diuji apakah \((\mu_1, \mu_2, \mu_3, \mu_4) = (48, 49, 50, 51)\)

data <- read.csv('https://raw.githubusercontent.com/farhanage/dataset-for-study/refs/heads/main/Analisis%20Multivariat/Tabel%203.7%20(Ramus%20Bone%20Length%20at%20Four%20Ages%20).csv', sep=';')[2:5]

head(data)
    y1   y2   y3   y4
1 47.8 48.8 49.0 49.7
2 46.4 47.3 47.7 48.4
3 46.3 46.8 47.8 48.5
4 45.1 45.3 46.1 47.2
5 47.6 48.5 48.9 49.3
6 52.5 53.2 53.3 53.7

Misalkan diketahui \(\pmb{\Sigma}\) adalah matrix diagonal dengan entri-entri diagonalnya bernilai 3.

mu <- c(48, 49, 50, 51)
n <- nrow(data)
p <- length(mu)

ybar <- colMeans(data)
Sigma <- diag(3, ncol=4, nrow=4)

Maka hitung statistik uji:

Z_sq <- n * t(ybar-mu) %*% solve(Sigma) %*% (ybar-mu)
Z_sq
         [,1]
[1,] 8.980333
qchisq(p=0.05, df=p, lower.tail = FALSE)
[1] 9.487729

Apa kesimpulannya?

Ketika Variansi Tidak Diketahui

Ketika variansi tidak diketahui, gunakan estimasi sampel dari \(\pmb{\Sigma}\) yaitu \(\textbf{S}\), di mana

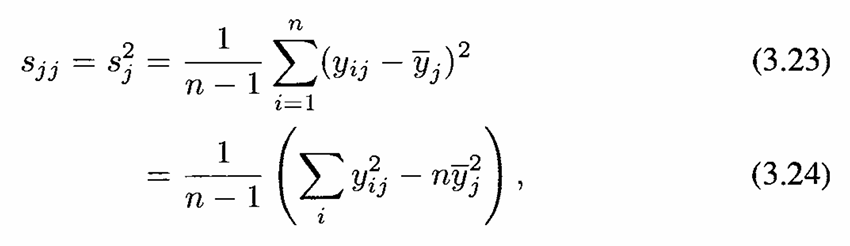
Uji yang digunakan adalah uji Hotelling’s \(T^2\), dengan statistik uji:

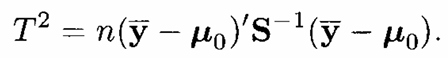
Tolak \(H_0\) pada taraf signifikansi \(\alpha\) jika \(T^2 > T^2_{\alpha, p, n-1}\)

Statistik uji \(T^2\) dapat dibawa ke distribusi \(F\) dengan hubungan:

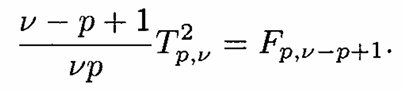
Dalam uji beda mean 1 sampel, nilai \(v\) adalah \(n-1\)

Implementasi Program

S <- cov(data)

T2 <- n * t(ybar - mu) %*% solve(S) %*% (ybar - mu)
T2
         [,1]
[1,] 1.792636

Cek nilai tabel \(T^2_{\alpha, p, n-1}\) di buku

Atau dengan Pendekatan distribusi F

F <- (n - p)/(n*p - p)*T2
F
         [,1]
[1,] 0.377397
# Titik kritis f
qf(0.05, p, n-p, lower.tail = FALSE)
[1] 3.006917
# Pvalue f
pf(F, p, n - p, lower.tail = FALSE)
          [,1]
[1,] 0.8214234
# Titik kritis T^2
((n*p - p)/(n - p))*qf(0.05, p, n-p, lower.tail = FALSE)
[1] 14.28286

Apa kesimpulannya?

Hotelling’s \(T^2\) Dengan Library

Penggunaan library kurang disarankan untuk pengerjaan karena proses penghitungan tidak terlihat, tetapi penggunaan library ini bagus untuk crosschecking jawaban kalian.

ICSNP::HotellingsT2(data, mu = mu, test = "f")

    Hotelling's one sample T2-test

data:  data
T.2 = 0.3774, df1 = 4, df2 = 16, p-value = 0.8214
alternative hypothesis: true location is not equal to c(48,49,50,51)

(Pastikan install library ICSNP)

Uji Beda Mean 2 Sampel Multivariat Independen

Dalam uji beda mean 2 sampel multivariat saling independen, hipotesis yang ingin kita uji adalah

\(H_0: \pmb{\mu_1} = \pmb{\mu_2}\)
\(H_1: \pmb{\mu_1} \neq \pmb{\mu_2}\)

dengan \(\pmb{\mu_1}\), \(\pmb{\mu_2}\) adalah vektor mean dari variabel-variabel sampel acak yang ingin diuji.

Statistik uji yang digunakan adalah:

dengan

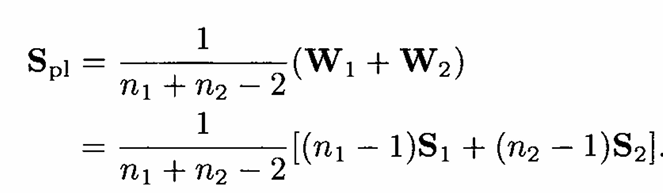
Tolak \(H_0\) pada taraf signifikansi \(\alpha\) jika \(T^2 \geq T^2_{\alpha, p, n_1+n_2-2}\)

atau dengan pendekatan distribusi \(F\)

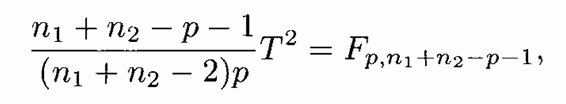
Implementasi Program

Gunakan tabel 5.9

data <- read.csv('https://raw.githubusercontent.com/farhanage/dataset-for-study/refs/heads/main/Analisis%20Multivariat/Tabel%205.9%20(Number%20of%20Words%20and%20Number%20of%20Verbs).csv', sep=';')

data
   Student  y1 y2  x1 x2
1        1 148 20 137 15
2        2 159 24 164 25
3        3 144 19 224 27
4        4 103 18 208 33
5        5 121 17 178 24
6        6  89 11 128 20
7        7 119 17 154 18
8        8 123 13 158 16
9        9  76 16 102 21
10      10 217 29 214 25
11      11 148 22 209 24
12      12 151 21 151 16
13      13  83  7 123 13
14      14 135 20 161 22
15      15 178 15 175 23

Akan diuji

\(H_0: \pmb{\mu_y} = \pmb{\mu_x}\)
\(H_1: \pmb{\mu_y} \neq \pmb{\mu_x}\)
y <- data[, 2:3]
y
    y1 y2
1  148 20
2  159 24
3  144 19
4  103 18
5  121 17
6   89 11
7  119 17
8  123 13
9   76 16
10 217 29
11 148 22
12 151 21
13  83  7
14 135 20
15 178 15
x <- data[, 4:5]
x
    x1 x2
1  137 15
2  164 25
3  224 27
4  208 33
5  178 24
6  128 20
7  154 18
8  158 16
9  102 21
10 214 25
11 209 24
12 151 16
13 123 13
14 161 22
15 175 23
n1 <- nrow(y)
n2 <- nrow(x)
p <- length(y)

# Vektor xbar ybar
ybar <- colMeans(y)
ybar
       y1        y2 
132.93333  17.93333 
xbar <- colMeans(x)
xbar
       x1        x2 
165.73333  21.46667 
# Matriks Sx dan Sy
Sy <- cov(y)
Sy
          y1       y2
y1 1405.7810 153.7095
y2  153.7095  28.6381
Sx <- cov(x)
Sx
          x1        x2
x1 1299.7810 137.34762
x2  137.3476  27.98095
# Hitung Spl
Spl <- 1/(n1 + n2 - 2) * ((n1 - 1) * Sy + (n2 - 1) * Sx)
Spl
          y1        y2
y1 1352.7810 145.52857
y2  145.5286  28.30952
# Hitung T^2
T2 <- (n1 * n2)/(n1 + n2) * t(ybar - xbar) %*% solve(Spl) %*% (ybar - xbar)
T2
         [,1]
[1,] 5.964616

Atau dengan bantuan library DescTools

library(DescTools)
HotellingsT2Test(y, x, test='chi')

    Hotelling's two sample T2-test

data:  y and x
T.2 = 5.9646, df = 2, p-value = 0.05068
alternative hypothesis: true location difference is not equal to c(0,0)

Uji t 2 Sampel Univariat Ketika H0 Ditolak

Ketika \(H_0\) ditolak, gunakan uji t 2 sampel pada masing-masing variabel

\(H_0: \mu_1 = \mu_2\)
\(H_1: \mu_1 \neq \mu_2\)

dengan statistik uji

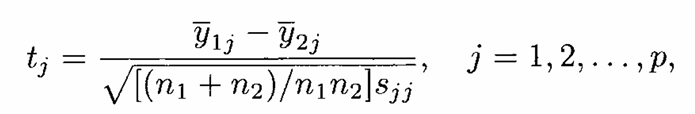
Tolak \(H_0\) pada taraf signifikansi \(\alpha\) jika \(|t| > t_{\alpha/2, n_1+n_2-2}\)

Implementasi Kode

t_values <- c()
p_values <- c()

for (i in 1:ncol(y)){
  test <- t.test(y[, i], x[, i], mu=0, var.equal=TRUE)
  t_values[i] <- test$statistic
  p_values[i] <- test$p.value
}

t_values
[1] -2.442253 -1.818649
# t penolakan
qt(0.025, n1+n2-2, lower.tail = FALSE)
[1] 2.048407
p_values
[1] 0.02116598 0.07967712

Kesimpulannya?

Uji Beda Mean 2 Sampel Berpasangan Multivariat

Tinjau data tabel 5.9 sebagai data berpasangan \((\pmb{y}, \pmb{x})\) di mana y dan x saling berkorelasi (dependen)

dapat dihitung selisih dari tiap variabel yang diukur (\(d\)):

data$d1 <- data$y1 - data$x1
data$d2 <- data$y2 - data$x2
data
   Student  y1 y2  x1 x2   d1  d2
1        1 148 20 137 15   11   5
2        2 159 24 164 25   -5  -1
3        3 144 19 224 27  -80  -8
4        4 103 18 208 33 -105 -15
5        5 121 17 178 24  -57  -7
6        6  89 11 128 20  -39  -9
7        7 119 17 154 18  -35  -1
8        8 123 13 158 16  -35  -3
9        9  76 16 102 21  -26  -5
10      10 217 29 214 25    3   4
11      11 148 22 209 24  -61  -2
12      12 151 21 151 16    0   5
13      13  83  7 123 13  -40  -6
14      14 135 20 161 22  -26  -2
15      15 178 15 175 23    3  -8

Untuk menguji

\(H_0: \pmb{\mu_y} = \pmb{\mu_x}\)
\(H_1: \pmb{\mu_y} \neq \pmb{\mu_x}\)

ekivalen dengan menguji

\(H_0: \pmb{\mu_d} = \pmb{0}\)
\(H_1: \pmb{\mu_d} \neq \pmb{0}\)

Menggunakan statistik uji

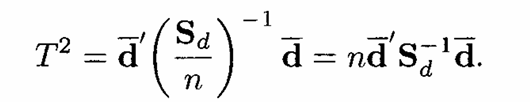
Tolak \(H_0\) pada taraf signifikansi \(\alpha\) jika \(T^2 > T^2_{\alpha, p, n-1}\)

Implementasi Kode

d <- y - x
d
     y1  y2
1    11   5
2    -5  -1
3   -80  -8
4  -105 -15
5   -57  -7
6   -39  -9
7   -35  -1
8   -35  -3
9   -26  -5
10    3   4
11  -61  -2
12    0   5
13  -40  -6
14  -26  -2
15    3  -8
dbar <- colMeans(d)
dbar
        y1         y2 
-32.800000  -3.533333 
Sd <- cov(d)
Sd
         y1        y2
y1 1096.029 139.90000
y2  139.900  31.55238
n <- nrow(d)
p <- length(d)

# Hitung T^2
T2 <- n * t(dbar) %*% solve(Sd) %*% dbar
T2
         [,1]
[1,] 15.19123

Latihan Soal