Pertemuan 6: Uji Randomization, Mann-Whitney, Smirnov, Squared Rank

Statistika Nonparametrik

Offline di Departemen Matematika
Published

November 19, 2024

Tabel Guide Uji Nonparametrik

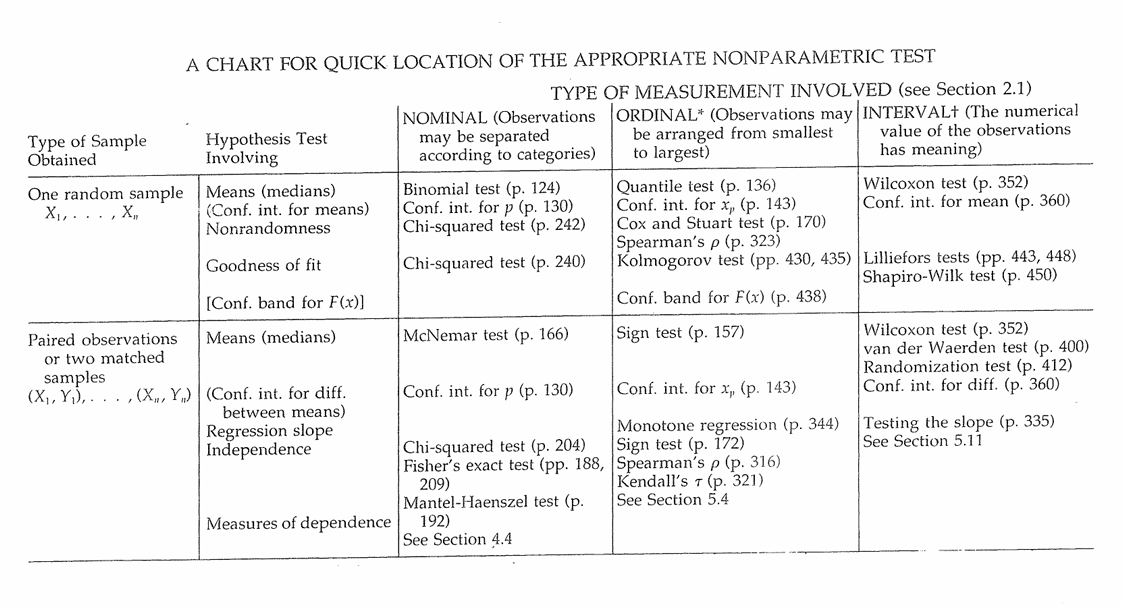
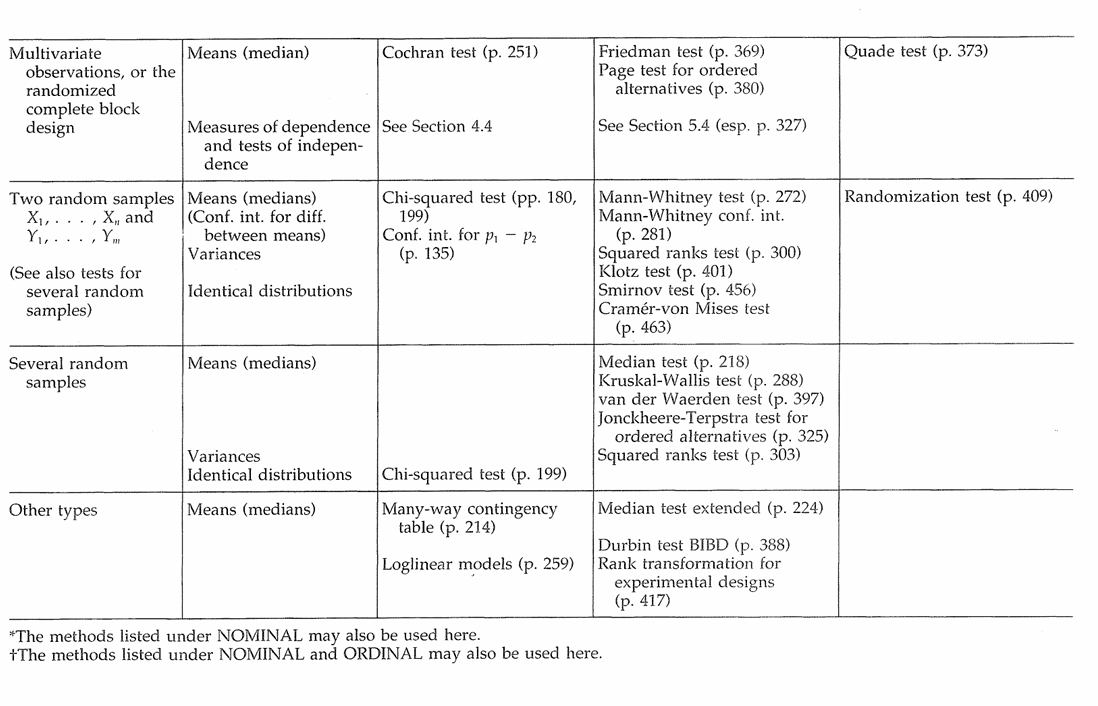
Fisher’s Randomization

  1. A tire company did a follow-up study on ten customers, randomly selected from those who had purchased new tires from them three years earlier, and asked them how many times they had encountered tire failure from any cause, such as nails, valve, leakage, etc. The study was restricted to two lines of long-life tires, called Brand A dan Bran B. These were their results.
Customer Brand A Brand B
1 0 3
2 2 5
3 0 1
4 1 4
5 2 3

Use Fisher’s randomization method to get the exact 𝑝-value for testing the null hypothesis of equal likelihood for tire failure, against the two sided alternative, that is, either Brand A or Brand B tends to have fewer tair values and a one-sided alternative that Brand A tends to have fewer tire failures.

  • Two Sided Alternative
\(H_0: E(X) = E(Y)\)
\(H_1: E(X) \neq E(Y)\)
## Bentuk vektor
A <- c(0, 2, 0, 1, 2)
B <- c(3, 5, 1, 4, 3)

## Hitung dimensi
n <- length(A)
m <- length(B)
## Bentuk list
X <- rep("X", n)
Y <- rep("Y", m)
group <- c(X,Y)
group
 [1] "X" "X" "X" "X" "X" "Y" "Y" "Y" "Y" "Y"

Dapat dicari semua kombinasi X dan Y dari group di atas menggunakan fungsi combn() dari library combinat

# install.packages("combinat")
library(combinat) 

## Hitung kombinasi
combn(group, n)

Sehingga jumlah kombinasi yang mungkin

n_kombinasi <- ncol(combn(group, n))
n_kombinasi
[1] 252

Didapat jumlah kelompok yang perlu dibentuk

## Hitung jumlah kelompok
round(n_kombinasi * 0.025)
[1] 6

Kombinasi jumlah kelompok yang mungkin

## Bentuk kombinasi
kombinasi <- unique(permn(group))

Gabungkan nilai-nilai yang mungkin dan urutkan dari yang terkecil

sorted_values <- sort(c(A,B))
sorted_values
 [1] 0 0 1 1 2 2 3 3 4 5

Fungsi Fisher’s Randomization from scratch

fisher_randomization <- function(kombinasi, sorted_values){
    result <- data.frame()

    for (i in 1:length(kombinasi)){
        T <- 0
        for (j in 1:length(kombinasi[[i]])){ 
            if (kombinasi[[i]][j] == 'X'){
                T <- T + sorted_values[j]
            } 
        }
        temp_df <- data.frame(matrix(c(kombinasi[[i]], T), nrow=1))
        result <- rbind(result, temp_df)
    }
    colnames(result) <- c(paste0(sorted_values), "T")
    result$T <- as.numeric(result$T) 
    result <- result[order(result$T), ]
    rownames(result) <- NULL
    
    return(result)
}  

result <- fisher_randomization(kombinasi, sorted_values)
head(result, n=6L)
  0 0 1 1 2 2 3 3 4 5 T
1 X X X X X Y Y Y Y Y 4
2 X X X X Y X Y Y Y Y 4
3 X X X Y X X Y Y Y Y 5
4 X X Y X X X Y Y Y Y 5
5 X X X X Y Y X Y Y Y 5
6 X X X X Y Y Y X Y Y 5

Maka didapat nilai T terbesar (\(w_{0.025}\)) = 5

Tolak \(H_0\) pada tingkat \(\alpha\) jika \(T_1 > W_{1-\alpha/2}\) atau \(T_1 < W_{\alpha/2}\)

T1 <- sum(A)
T1
[1] 5

Kesimpulannya?

Hitung exact p-value:

less_T1 <- result[result$T < 5, 'T']
less_T1
[1] 4 4
p_val <- 2 *  sum(less_T1)/ n_kombinasi
p_val
[1] 0.06349206

Kesimpulannya?

  • One Sided Alternative

Use \(w_{0.05}\) and reject \(H_0\) when \(T_1 < w_{0.05}\)

Latihan Soal

  1. A random sample of eight adults were asked how old they were when they went on their first date. The three men responded with ages 15, 17, 16, while the five women answered 12, 14, 15, 10, and 12. Test the hypothesis that the average is the same for both sexes against the alternative that girls tend to be younger on the occasion of their first date.

Uji Mann-Whitney

  1. The senior class in a particular high school had 48 boys. Twelve boys lived on farms and the other 36 lived in town. A test was devised to see if farm boys in general were more physically fit than town boys. Each boy in the class was given a physical fitness test in which a low score indicates poor physical condition. The scores of the farm boys (\(X_i\)) and the town boys (\(Y_i\)) are as follows.

## Bentuk vektor dari setiap grup
farm <- c(14.8, 7.3, 5.6, 6.3, 9, 4.2, 10.6, 12.5, 12.9, 16.1, 11.4, 2.7) #x
town <- c(12.7, 14.2, 12.6, 2.1, 17.7, 11.8, 16.9, 7.9, 16, 10.6, 5.6, 5.6, 7.6,
          11.3, 8.3, 6.7, 3.6, 1, 2.4, 6.4, 9.1, 6.7, 18.4, 3.2, 6.2, 6.1, 15.3,
          10.6, 1.8, 5.9, 9.9, 10.6, 14.8, 5, 2.6, 4) #y

Bentuk tabel untuk menghitung rank

## Lakukan dengan uji manual
### Farm
temp <- farm
category <- rep("Farm", length(temp))
df1 <- data.frame(temp, category) 

### Town
temp <- town
category <- rep("Town", length(temp))
df2 <- data.frame(temp, category)

### Gabungan
df <- rbind(df1, df2)
df <- df[order(df$temp), ]
df$rank <- rank(df$temp)
df$x <- ifelse(df$category == "Farm", df$temp, 0)
df$y <- ifelse(df$category == "Town", df$temp, 0)

df
   temp category rank    x    y
30  1.0     Town  1.0  0.0  1.0
41  1.8     Town  2.0  0.0  1.8
16  2.1     Town  3.0  0.0  2.1
31  2.4     Town  4.0  0.0  2.4
47  2.6     Town  5.0  0.0  2.6
12  2.7     Farm  6.0  2.7  0.0
36  3.2     Town  7.0  0.0  3.2
29  3.6     Town  8.0  0.0  3.6
48  4.0     Town  9.0  0.0  4.0
6   4.2     Farm 10.0  4.2  0.0
46  5.0     Town 11.0  0.0  5.0
3   5.6     Farm 13.0  5.6  0.0
23  5.6     Town 13.0  0.0  5.6
24  5.6     Town 13.0  0.0  5.6
42  5.9     Town 15.0  0.0  5.9
38  6.1     Town 16.0  0.0  6.1
37  6.2     Town 17.0  0.0  6.2
4   6.3     Farm 18.0  6.3  0.0
32  6.4     Town 19.0  0.0  6.4
28  6.7     Town 20.5  0.0  6.7
34  6.7     Town 20.5  0.0  6.7
2   7.3     Farm 22.0  7.3  0.0
25  7.6     Town 23.0  0.0  7.6
20  7.9     Town 24.0  0.0  7.9
27  8.3     Town 25.0  0.0  8.3
5   9.0     Farm 26.0  9.0  0.0
33  9.1     Town 27.0  0.0  9.1
43  9.9     Town 28.0  0.0  9.9
7  10.6     Farm 30.5 10.6  0.0
22 10.6     Town 30.5  0.0 10.6
40 10.6     Town 30.5  0.0 10.6
44 10.6     Town 30.5  0.0 10.6
26 11.3     Town 33.0  0.0 11.3
11 11.4     Farm 34.0 11.4  0.0
18 11.8     Town 35.0  0.0 11.8
8  12.5     Farm 36.0 12.5  0.0
15 12.6     Town 37.0  0.0 12.6
13 12.7     Town 38.0  0.0 12.7
9  12.9     Farm 39.0 12.9  0.0
14 14.2     Town 40.0  0.0 14.2
1  14.8     Farm 41.5 14.8  0.0
45 14.8     Town 41.5  0.0 14.8
39 15.3     Town 43.0  0.0 15.3
21 16.0     Town 44.0  0.0 16.0
10 16.1     Farm 45.0 16.1  0.0
19 16.9     Town 46.0  0.0 16.9
17 17.7     Town 47.0  0.0 17.7
35 18.4     Town 48.0  0.0 18.4

Hitung Statistik Uji

### Statistik Uji
(T.stat <- sum(df[df$category == "Farm", ]$rank))
[1] 321
n <- length(farm)
m <- length(town)
N <- n + m
r_sq <- sum(df$rank^2)
r_sq
[1] 38016
T1 <- (T.stat - n*((N + 1)/2))/sqrt((n*m*r_sq/(N*(N - 1)) - n*m*(N + 1)^2/(4*(N - 1)))) 
T1
[1] 0.6431365
  • Upper tailed, H0 ditolak: \(T_1 > z_{1-\alpha}\)
  • Lower tailed, H0 ditolak: \(T_1 < z_\alpha\)
  • Two tailed, H0 ditolak: \(T_1 < z_{\alpha/2}\) atau \(T_1 > z_{1-\alpha/2}\)
# Upper Tail - Kuantil ke 0.95 dari N(0,1)
qnorm(.95)
[1] 1.644854

Kesimpulannya?

Latihan Soal

  1. Misalkan terdapat suatu klaim yang mengatakan bahwa tanaman A memiliki khasiat dalam membantu mengurangi gejala medis suatu penyakit sistem pencernaan manusia. Kemudian, Anda diminta untuk mengecek kebenaran mengenai klaim tersebut. Setelah beberapa saat, Anda mendapatkan data mengenai 20 pasien penyakit pencernaan sebagai berikut!
Kontrol 3 6 4 5 5 8 6 5 7 2
Obat A 2 3 1 4 7 5 5 4 2 1

Dalam kasus ini, apa uji yang cocok untuk melihat signifikansi perbedaan antara pasien kelompok kontrol dengan pasien yang diberikan obat dari tanaman A? Apa saja asumsi yang perlu dipenuhi uji yang Anda pilih? Lakukanlah uji yang Anda pilih tersebut! Definisikan secara lengkap hipotesis, prosedur uji statistik, hingga keputusan dan kesimpulan yang dapat diambil dari uji tersebut! Gunakan taraf signifikansi 0.05!

Uji Smirnov

  1. Manajer sumber daya alam telah mencoba menggunakan Satellite Landsat Multispectral Scanner data untuk klasifikasi tutupan lahan yang lebih baik. Saat satelit itu diketahui terbang di atas wilayah yang berupa hutan, intensitas cahaya dibaca kemudian direkam pada pita inframerah. Diperoleh sampel yang sudah diurut seperti berikut:

77 77 78 78 81 81 82 82 82 82 82 83 83 84 84 84 84 85 86 86 86 86 86 87 87 87 87 87 87 87 89 89 89 89 89 89 89 90 90 90 91 91 91 91 91 91 91 91 91 91 93 93 93 93 93 93 94 94 94 94 94 94 94 94 94 94 94 94 95 95 95 95 95 96 96 96 96 96 96 97 97 97 97 97 97 97 97 97 98 99 100 100 100 100 100 100 100 100 100 101 101 101 101 101 101 102 102 102 102 102 102 103 103 104 104 104 105 107

Saat satelit itu terbang di atas wilayah perkotaan, intensitas cahaya yang dipantulkan oleh pita infra merah yang telah diurut seperti berikut:

71 72 73 74 75 77 78 79 79 79 79 80 80 80 81 81 81 82 82 82 82 84 84 84 84 84 84 85 85 85 85 85 85 86 86 87 88 90 91 94

Jika arti pembacaan berbeda, maka bacaan tersebut dapat digunakan untuk membedakan intensitas wilayah perkotaan dari kawasan hutan

Uji kolmogorov-smirnov dapat dilakukan dengan memanggil fungsi ks.test() dari library dgof

# install.packages("dgof")
library(dgof)
Warning: package 'dgof' was built under R version 4.4.1

Attaching package: 'dgof'
The following object is masked from 'package:stats':

    ks.test
hutan <- c(77, 77, 78, 78, 81, 81, 82, 82, 82, 82, 82, 83, 83, 84, 84, 84, 84,
           85, 86, 86, 86, 86, 86, 87, 87, 87, 87, 87, 87, 87, 89, 89, 89, 89,
           89, 89, 89, 90, 90, 90, 91, 91, 91, 91, 91, 91, 91, 91, 91, 91, 93,
           93, 93, 93, 93, 93, 94, 94, 94, 94, 94, 94, 94, 94, 94, 94, 94, 94,
           95, 95, 95, 95, 95, 96, 96, 96, 96, 96, 96, 97, 97, 97, 97, 97, 97,
           97, 97, 97, 98, 99, 100, 100, 100, 100, 100, 100, 100, 100, 100, 101,
           101, 101, 101, 101, 101, 102, 102, 102, 102, 102, 102, 103, 103, 104,
           104, 104, 105, 107)
kota <- c(71, 72, 73, 74, 75, 77, 78, 79, 79, 79, 79, 80, 80, 80, 81, 81, 81,
          82, 82, 82, 82, 84, 84, 84, 84, 84, 84, 85, 85, 85, 85, 85, 85, 86,
          86, 87, 88, 90, 91, 94)

ks.test(hutan, kota, alternative = 'two.sided')
Warning in ks.test(hutan, kota, alternative = "two.sided"): cannot compute
correct p-values with ties

    Two-sample Kolmogorov-Smirnov test

data:  hutan and kota
D = 0.68008, p-value = 1.994e-12
alternative hypothesis: two-sided

Latihan Soal

  1. Diet A was given to four overweight girls and diet B was given to five other overweight girls, with the following observed weight losses. Find a 90% confidence interval for mean difference in effectiveness of the two diets.
Diet Weight Losses (pounds)
A 7, 2, -1, 4
B 6, 5, 2, 8, 3

Uji Squared Rank

  1. Suatu perusahaan pengemasan makanan ingin mengetahui apakah kotak sereal yang diproduksi benar-benar mengandung setidaknya sesuai dengan sejumlah ons sereal yang tertera di kemasan. Dalam hal ini, harus ditentukan jumlah rata-rata per kotak sedikit lebih banyak dari jumlah yang tertera karena variasi yang disebabkan oleh mesin pengemas yang terkadang memasukkan sereal dengan jumlah yang lebih sedikit atau lebih banyak. Mesin dengan variasi yang lebih kecil akan lebih menguntungkan perusahaan karena jumlah sereal yang dimasukkan bisa lebih mendekati jumlah yang ditentukan. Sebuah mesin baru diuji untuk dilihat apakah memiliki variansi yang lebih kecil dari mesin yang lama. Beberapa kotak diisi sereal dengan mesin yang lama kemudian jumlah sereal pada setiap kotak diukur. Hal yang sama dilakukan pada mesin yang baru. Didapat data sebagai berikut
Present (X) 10,8 11,1 10,4 10,1 11,3
New (Y) 10,8 10,5 11 10,9 10,8 10,7 10,8 
## Bentuk vektor
present <- c(10.8, 11.1, 10.4, 10.1, 11.3) #X
new <- c(10.8, 10.5, 11, 10.9, 10.8, 10.7, 10.8) #Y

## Present
temp <- present
Xbar <- mean(temp)
category <- rep("Present", length(temp))
temp_absdev <- abs(temp - mean(temp))
df1 <- data.frame(temp, category, temp_absdev) 

## New
temp <- new
Ybar <- mean(temp)
category <- rep("New", length(temp))
temp_absdev <- abs(temp - mean(temp))
df2 <- data.frame(temp, category, temp_absdev)

## Gabungan
df <- rbind(df1, df2)
df <- df[order(df$temp_absdev), ]
df$rank <- rank(df$temp_absdev)
df$sqrank <- rank(df$temp_absdev)^2

## Statistik Uji
T.stat <- sum(df[df$category == "Present", ]$sqrank)
n <- length(present)
m <- length(new)
N <- n + m
rsq_bar <- mean(df$sqrank)
r_qt <- sum(df$sqrank^2)

T1 <- (T.stat - n*rsq_bar)/sqrt(n*m*r_qt/(N*(N-1)) - n*m*(rsq_bar^2)/(N-1))
T1
[1] 2.327331
  • Upper tailed, H0 ditolak: \(T_1 > z_{1-\alpha}\)
  • Lower tailed, H0 ditolak: \(T_1 < z_\alpha\)
  • Two tailed, H0 ditolak: \(T_1 < z_{\alpha/2}\) atau \(T_1 > z_{1-\alpha/2}\)
# Upper Tail - Kuantil ke 0.95 dari N(0,1)
qnorm(.95)
[1] 1.644854

Kesimpulannya?

Latihan Soal

  1. A blood bank kept a record of the rate of heartbeats for several blood donors.
Men Women
58 66
76 74
82 69
74 76
79 72
65 73
74 75
86 67
68

Is the variation among the men significantly greater than the variation among women?