(Pertemuan 06) Distribusi Kontinu di R, Distribusi di Excel

Continuous Distributions in R, Distributions in Excel

Offline di Departemen Matematika

Kembali ke Pengantar Sains Data

Melanjutkan dari pertemuan sebelumnya tentang distribusi diskirt di R, pada pertemuan kali ini, kita akan membahas tentang beberapa distribusi kontinu di R, tepatnya distribusi uniform (kontinu) dan distribusi normal, baik dengan base R ataupun dengan distr. Kemudian, kita juga akan membahas tentang distribusi probabilitas di Excel, baik diskrit maupun kontinu, terutama cara menghasilkan data random menggunakan Analysis ToolPak.

Distribusi Kontinu dengan base R

Sebenarnya ada banyak distribusi kontinu. Namun, sesuai dengan batasan materi kuliah Pengantar Sains Data, kita hanya akan membahas dua distribusi kontinu, yaitu

• distribusi uniform (kontinu), dan

• distribusi normal.

Kalian akan mempelajari lebih banyak distribusi, baik distribusi diskrit maupun distribusi kontinu, serta berbagai macam “penggabungannya”, di mata kuliah Statistika Matematika 1.

Seperti biasa, kita masih bermain dengan fungsi d…, p,…, q…, dan r… yang bisa kita ingat kembali:

• d… melambangkan PDF

• p… melambangkan CDF

• q… melambangkan inverse CDF atau fungsi kuantil (quantile function)

• r… melambangkan RNG (random number generator)

Distribusi Normal

Sesuai namanya, distribusi normal sering dijumpai di kehidupan sehari-hari; tidak jarang terjadi, persebaran berbagai data, yang awalnya terkesan acak, ternyata mendekati distribusi normal.

Distribusi normal memiliki dua parameter, yaitu

• rata-rata atau mean \(\mu\) (mu)

• variansi atau variance \(\sigma^2\) (sigma kecil, dikuadratkan), yang harus taknegatif (nonnegative)

  Catatan: sigma besar adalah \(\Sigma\) yang biasa kita gunakan untuk notasi penjumlahan atau sumasi.

Perhatikan bahwa rata-rata termasuk ukuran pemusatan data, sedangkan variansi termasuk ukuran persebaran data (juga disebut keragaman data). Nilai kedua parameter tersebut bisa diubah-ubah sesuai keperluan. Dengan demikian, distribusi normal bisa cukup fleksibel menyesuaikan dengan berbagai macam data.

Apabila suatu variabel acak \(X\) mengikuti distribusi normal, biasa ditulis

\[X \sim N(\mu, \sigma^2)\]

Namun, daripada berdasarkan rata-rata dan variansi, terkadang suatu distribusi normal ditentukan berdasarkan rata-rata dan simpangan baku (standard deviation), biasa disingkat sd, std, stdev, atau stddev, dan biasa dilambangkan \(\sigma\), yang merupakan akar dari variansi. Di R, standard deviation biasa dilambangkan sd.

Perbedaan antara variansi dan standard deviation hanyalah masalah kuadrat. Berhati-hati saja.

Selain itu, perlu diingat bahwa penulisan

\[X \sim N(\mu, \sigma^2)\]

selalu menggunakan variansi yaitu \(\sigma^2\), daripada standard deviation.

Support dari distribusi normal adalah keseluruhan garis bilangan real (the real line), yaitu interval buka \((-\infty, \infty)\)

PDF

Untuk \(-\infty < x < \infty\), PDF dari distribusi normal bisa ditulis

\[n(x; \mu, \sigma) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}\frac{(x-\mu)^2}{\sigma^2}}\]

Perhatikan, ada konstanta \(\pi\) (pi) dan konstanta Euler \(e\). Kedua konstanta tersebut tersedia di R:

pi

[1] 3.141593

exp(1)

[1] 2.718282

Sebenarnya, exp adalah fungsi eksponensial \(e^x\).

Distribusi normal standar (standard normal distribution) adalah distribusi normal istimewa, yang memiliki parameter \(\mu = 0\) dan parameter \(\sigma = 1\), atau bisa dilambangkan \(N(0,1)\).

dnorm(1.3,
      mean = 0,
      sd = 1)

[1] 0.1713686

Untuk plotting, kita tidak perlu menggunakan keseluruhan support (mustahil juga), karena untuk nilai-nilai yang tidak dekat dengan nilai tengah atau rata-rata, probabilitasnya hampir nol. Oleh karena itu, kita cukup memilih interval yang memuat titik-titik yang dekat dengan rata-rata, misal \(0 \pm 4\), tidak perlu terlalu besar.

x_norm_1 <- seq(0-4, 0+4, length = 100)
x_norm_1

  [1] -4.00000000 -3.91919192 -3.83838384 -3.75757576 -3.67676768 -3.59595960
  [7] -3.51515152 -3.43434343 -3.35353535 -3.27272727 -3.19191919 -3.11111111
 [13] -3.03030303 -2.94949495 -2.86868687 -2.78787879 -2.70707071 -2.62626263
 [19] -2.54545455 -2.46464646 -2.38383838 -2.30303030 -2.22222222 -2.14141414
 [25] -2.06060606 -1.97979798 -1.89898990 -1.81818182 -1.73737374 -1.65656566
 [31] -1.57575758 -1.49494949 -1.41414141 -1.33333333 -1.25252525 -1.17171717
 [37] -1.09090909 -1.01010101 -0.92929293 -0.84848485 -0.76767677 -0.68686869
 [43] -0.60606061 -0.52525253 -0.44444444 -0.36363636 -0.28282828 -0.20202020
 [49] -0.12121212 -0.04040404  0.04040404  0.12121212  0.20202020  0.28282828
 [55]  0.36363636  0.44444444  0.52525253  0.60606061  0.68686869  0.76767677
 [61]  0.84848485  0.92929293  1.01010101  1.09090909  1.17171717  1.25252525
 [67]  1.33333333  1.41414141  1.49494949  1.57575758  1.65656566  1.73737374
 [73]  1.81818182  1.89898990  1.97979798  2.06060606  2.14141414  2.22222222
 [79]  2.30303030  2.38383838  2.46464646  2.54545455  2.62626263  2.70707071
 [85]  2.78787879  2.86868687  2.94949495  3.03030303  3.11111111  3.19191919
 [91]  3.27272727  3.35353535  3.43434343  3.51515152  3.59595960  3.67676768
 [97]  3.75757576  3.83838384  3.91919192  4.00000000

plot(x_norm_1,
     dnorm(x_norm_1, mean = 0, sd = 1),
     type = 'o')

Contoh distribusi normal yang lain: \(N(2,5)\)

dnorm(2.7,
      mean = 2,
      sd = 5)

[1] 0.07901035

Ternyata, nilai untuk distribusi normal dengan parameter lain bisa diperoleh dari distribusi normal standar, memanfaatkan yang namanya Z-score.

\[Z = \frac{X-\mu}{\sigma}\]

Namun, ketika menghitung PDF dan sudah memperoleh hasil dari distribusi normal standar, kita perlu membagi lagi hasilnya dengan standard deviation yang aslinya, karena ada masalah scaling (skala).

Misalnya, untuk \(X=2.7\) dan \(X \sim N(2,5)\),

\[Z = \frac{X-2}{5} = \frac{2.7-2}{5}\]

Namun, daripada sekadar menghitung

dnorm((2.7-2)/(5),
      mean = 0,
      sd = 1)

[1] 0.3950517

kita harus membagi lagi dengan standard deviation yang aslinya yaitu 5, sebagai berikut:

dnorm((2.7-2)/(5),
      mean = 0,
      sd = 1)/5

[1] 0.07901035

Bandingkan:

dnorm(2.7,
      mean = 2,
      sd = 5)

[1] 0.07901035

Sama, ya!

Untuk membuat plot dari \(N(2,5)\), kita buat titik-titik x_norm_2 sedemikian sehingga nilai-nilainya berada di sekitar rata-rata 2, tetapi dengan interval yang lebih luas, misal \(2 \pm 20\), karena standard deviation yang lebih besar dibandingkan dengan membuat plot \(N(0,1)\) tadi.

x_norm_2 <- seq(2-20, 2+20, length = 100)
x_norm_2

  [1] -18.0000000 -17.5959596 -17.1919192 -16.7878788 -16.3838384 -15.9797980
  [7] -15.5757576 -15.1717172 -14.7676768 -14.3636364 -13.9595960 -13.5555556
 [13] -13.1515152 -12.7474747 -12.3434343 -11.9393939 -11.5353535 -11.1313131
 [19] -10.7272727 -10.3232323  -9.9191919  -9.5151515  -9.1111111  -8.7070707
 [25]  -8.3030303  -7.8989899  -7.4949495  -7.0909091  -6.6868687  -6.2828283
 [31]  -5.8787879  -5.4747475  -5.0707071  -4.6666667  -4.2626263  -3.8585859
 [37]  -3.4545455  -3.0505051  -2.6464646  -2.2424242  -1.8383838  -1.4343434
 [43]  -1.0303030  -0.6262626  -0.2222222   0.1818182   0.5858586   0.9898990
 [49]   1.3939394   1.7979798   2.2020202   2.6060606   3.0101010   3.4141414
 [55]   3.8181818   4.2222222   4.6262626   5.0303030   5.4343434   5.8383838
 [61]   6.2424242   6.6464646   7.0505051   7.4545455   7.8585859   8.2626263
 [67]   8.6666667   9.0707071   9.4747475   9.8787879  10.2828283  10.6868687
 [73]  11.0909091  11.4949495  11.8989899  12.3030303  12.7070707  13.1111111
 [79]  13.5151515  13.9191919  14.3232323  14.7272727  15.1313131  15.5353535
 [85]  15.9393939  16.3434343  16.7474747  17.1515152  17.5555556  17.9595960
 [91]  18.3636364  18.7676768  19.1717172  19.5757576  19.9797980  20.3838384
 [97]  20.7878788  21.1919192  21.5959596  22.0000000

plot(x_norm_2,
     dnorm(x_norm_2, mean = 2, sd = 5),
     type = 'o')

Untuk distribusi kontinu, perhitungan probabilitas harus melalui CDF, sedangkan PDF hanya menggambarkan bentuk distribusi.

Tidak seperti distribusi diskrit, PDF distribusi kontinu di \(\mathbf{x}\) TIDAK SAMA DENGAN \(\mathbf{\text{Pr}(X=x)}\). Bahkan, di distribusi kontinu, untuk tiap \(x\) selalu berlaku

\[\text{Pr}(X=x) = 0\]

Mengapa demikian? Misalnya, untuk distribusi normal, kita ingin menghitung \(\text{Pr}(X=2.7)\). Artinya, kita meminta probabilitas bahwa nilai yang kita peroleh adalah tepat 2.7, tidak boleh meleset sedikitpun. Kalau kita memperoleh misalnya 2.7000000001, itu sudah dianggap angka yang berbeda. Tentunya, memperoleh persis suatu angka tertentu sangat tidak realistis, sehingga probabilitasnya adalah nol.

Dengan demikian, untuk distribusi kontinu, probabilitas di tepat satu titik, di titik apapun, itu selalu nol.

Kalau begitu, apakah probabilitas bahwa kita dapat nilai apapun sama sekali itu adalah nol, sehingga tidak ada yang mungkin? Tidak juga. Mungkin terdengar aneh. Namun, sebenarnya, untuk distribusi kontinu, daripada menghitung probabilitas memperoleh tepat suatu nilai tertentu, kita biasa menghitung probabilitas memperoleh nilai di interval tertentu. Dengan begitu, barulah probabilitasnya taknol.

Sebagaimana di distribusi diskrit, kita bisa menghitung probabilitas untuk rentang atau interval tertentu menggunakan CDF. Oleh karena itulah, perhitungan probabilitas untuk distribusi kontinu selalu menggunakan CDF, tidak pernah menggunakan PDF.

CDF

pnorm(1.96,
      mean = 0,
      sd = 1)

[1] 0.9750021

plot(x_norm_1,
     pnorm(x_norm_1, mean = 0, sd = 1),
     type = 'o')

Contoh:

Misalkan \(X\) merupakan variabel acak yang berdistribusi normal dengan \(\mu = 50\) dan variansi standard deviation \(\sigma = 10\). Hitunglah

\[\text{Pr}(45 < X < 62)\]

Jawab:

Perhatikan bahwa

\[\begin{align*} \text{Pr}&(45 < X < 62) \\ &= \text{Pr}(X < 62) - \text{Pr}(X \leq 45) \\ &= \text{Pr}(X \leq 62) - \text{Pr}(X \leq 45) \end{align*}\]

karena

\[\begin{align*} \text{Pr}&(X < 62) \\ &= \text{Pr}(X \leq 62) - \text{Pr}(X = 62) \\ &= \text{Pr}(X \leq 62) - 0 \\ &= \text{Pr}(X \leq 62) \end{align*}\]

Sehingga, \(\text{Pr}(45 < X < 62)\) bisa dihitung dengan

\[\text{Pr}(X \leq 62) - \text{Pr}(X \leq 45)\]

yaitu selisih dua nilai CDF:

pnorm(62, mean = 50, sd = 10) -
  pnorm(45, mean = 50, sd = 10)

[1] 0.5763928

Kesimpulannya,

\[\text{Pr}(45 < X < 62) \approx 0.5763928\]

Cara lain, kita bisa juga memanfaatkan Z-score. Misalkan

\[Z = \frac{X-\mu}{\sigma} = \frac{X-50}{10}\]

Maka

\[\begin{align*} \text{Pr}&(45 < X < 62) \\ &= \text{Pr}\left(\frac{45-50}{10} < \frac{X-50}{10} < \frac{62-50}{10}\right) \\ &= \text{Pr}\left(\frac{45-50}{10} < Z < \frac{62-50}{10}\right) \\ &= \text{Pr}\left(Z \leq \frac{62-50}{10}\right) - \text{Pr}\left(Z \leq \frac{45-50}{10}\right) \end{align*}\]

Sehingga kita tinggal menghitung:

pnorm((62-50)/10, mean = 0, sd = 1) -
  pnorm((45-50)/10, mean = 0, sd = 1)

[1] 0.5763928

Daripada langsung mengetik sepanjang itu, kita juga bisa menghitung dulu

(62-50)/10

[1] 1.2

(45-50)/10

[1] -0.5

baru memasukkan,

\[\begin{align*} \text{Pr}&(45 < X < 62) \\ &= \text{Pr}\left(Z \leq \frac{62-50}{10}\right) - \text{Pr}\left(Z \leq \frac{45-50}{10}\right) \\ &= \text{Pr}\left(Z \leq 1.2\right) - \text{Pr}\left(Z \leq -0.5\right) \end{align*}\]

sehingga bisa dihitung

pnorm(1.2, mean = 0, sd = 1) -
  pnorm(-0.5, mean = 0, sd = 1)

[1] 0.5763928

Apabila sewaktu-waktu kalian perlu menghitung ini tetapi tidak bisa mengakses R, kalian bisa memanfaatkan tabel normal standar (standard normal table), yaitu tabel yang mendata berbagai nilai CDF untuk distribusi normal standar yaitu \(N(0,1)\), dan kebetulan juga disebut tabel Z-score. Carilah nilai CDF untuk \(Z=1.2\) dan nilai CDF untuk \(Z=-0.5\), lalu hitung selisihnya.

Apabila menggunakan mean = 0 dan sd = 1, kalian juga bisa saja menganggap fungsi pnorm sebagai fungsi untuk memperoleh nilai pada tabel normal standar. Misalnya, nilai di \(Z=1.2\) adalah

pnorm(1.2, mean = 0, sd = 1)

[1] 0.8849303

dan nilai di \(Z=-0.5\) adalah

pnorm(-0.5, mean = 0, sd = 1)

[1] 0.3085375

Silakan bandingkan dengan tabel normal standar, yang misalnya bisa kalian temukan di lampiran buku pengantar statistik seperti karangan Walpole.

Quantile function

Misalkan diketahui \(X \sim N(0,1)\) dan

\[\text{Pr}(X \leq x) = 0.975\]

Bagaimana cara menentukan \(x\)?

Perhatikan bahwa, fungsi probabilitas seperti di atas melambangkan CDF, dan kita ingin mencari nilai \(x\) yang membuat nilai CDF menjadi 0.975. Caranya, kita bisa menggunakan inverse CDF atau quantile function, sebagai berikut.

qnorm(0.975,
      mean = 0,
      sd = 1)

[1] 1.959964

Ternyata, nilai \(x\) yang diinginkan sekitar 1.96.

Kalau ragu, kita bisa periksa dengan menghitung nilai CDF untuk \(x=1.96\)

pnorm(1.96,
      mean = 0,
      sd = 1)

[1] 0.9750021

Benar ya!

Tentunya, mean tidak harus nol dan sd tidak harus satu. Contohnya, apabila diketahui

\[X \sim N(2,5), \quad \text{Pr}(X=x) = 0.73\]

maka kita bisa memperoleh \(x\) dengan qnorm yaitu inverse CDF

qnorm(0.73, mean = 2, sd = 5)

[1] 5.064065

Sehingga \(x \approx 5.064\), yang bisa kita periksa dengan pnorm yaitu CDF

pnorm(5.064, mean = 2, sd = 5)

[1] 0.7299957

Cukup dekat.

RNG

set.seed(62)
n <- 100
random_normal_1 <- rnorm(n, mean = 0, sd = 1)
random_normal_1

  [1]  0.801270126  0.284456708 -1.512796984  0.074637826  2.260744864
  [6]  0.061994083  0.913783028 -1.201950117  0.096915709 -0.986658430
 [11] -0.945597948  1.066644680  0.320424359 -1.547620322 -0.973418633
 [16] -0.044839783  1.100497403  0.643893414  1.158084038 -0.104914360
 [21] -1.392449727  1.018245804  0.826401081  1.289595050 -0.643231482
 [26] -0.001173311 -1.948468606  0.680949495  0.274233523 -1.905682922
 [31] -1.207395634  0.379645715 -0.832700980 -1.480467865  1.045205002
 [36]  1.203374466  1.143497941 -0.798450844  0.713542224  0.014509402
 [41]  1.065312134 -0.162379461 -0.733018312  0.283498988 -0.193434842
 [46]  1.548665726  0.277543508 -0.769101533  1.571636889  1.300682395
 [51]  0.049887057 -0.417278907  0.188247814  1.011823237  0.819801179
 [56]  0.526496313 -1.473395423 -0.686042765 -0.374751726  1.149207414
 [61]  0.309402632 -1.248579103  0.082461577  3.079093309 -1.043472726
 [66]  2.608787079 -0.223155112  0.277967984  1.341954354 -1.037490047
 [71] -0.382641299  1.068881533 -1.840465410 -0.557030007  0.566990033
 [76]  2.232051009 -0.309609288  1.386739199 -0.428271844 -0.655081698
 [81] -0.323856515 -0.071806893 -0.604127858 -0.117262945 -0.356753720
 [86]  1.342047477 -0.626166768  0.374192123 -0.370055470 -0.361204965
 [91]  0.773178206 -1.322378159  2.213237411  1.095148834 -0.155491552
 [96]  1.086000546 -0.446262004  0.399248471 -0.553159488 -0.596143996

Untuk distribusi kontinu, tidak mungkin kita buat bar plot, karena banyaknya elemen di support sudah infinite (tak berhingga), bahkan uncountable (tak terhitung).

Kita bisa membuat histogram,

hist(random_normal_1)

yang kemudian bisa kita kostumisasi (maksudnya customize) atau ubah-ubah opsinya:

hist(random_normal_1,
     breaks = 7,
     main = "Histogram 100 sampel dari N(0,1)",
     xlab = "Nilai X",
     ylab = "Banyaknya sampel",
     col = "orange")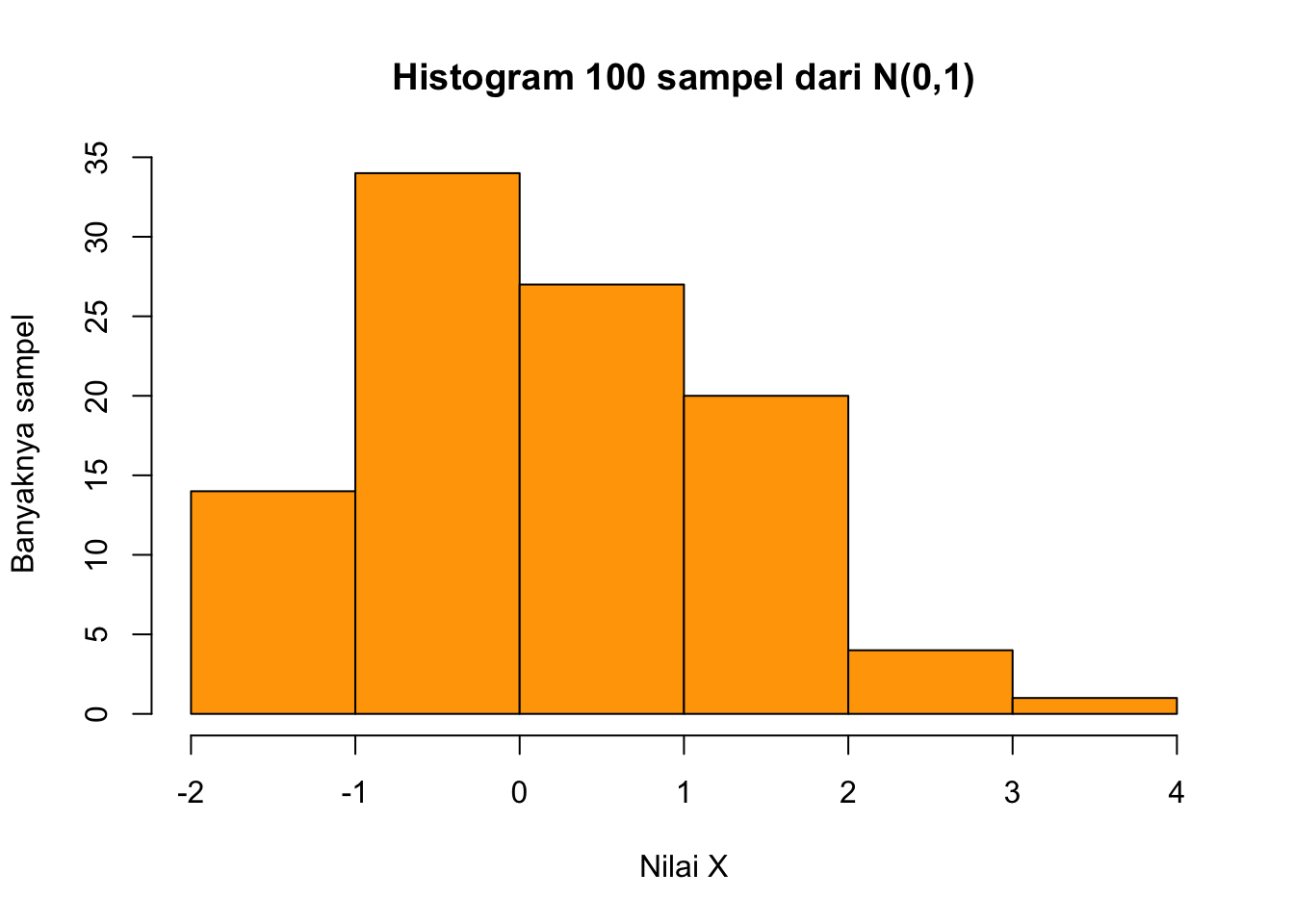

Untuk distribusi kontinu, selain membuat histogram, kita juga bisa membuat yang namanya density plot. Intinya, ini adalah perkiraan bentuk distribusi kontinu berdasarkan data yang diberikan. Dalam hal ini, dengan data random yang kita miliki, kita bisa mencoba membentuk kembali perkiraan bentuk distribusi aslinya, yakni distribusi normal.

plot(density(random_normal_1),
     main = "density plot: normal, mean 0, sd 1")

Cukup dekat, ya! Memang tidak sempurna, karena penarikan data atau sampling yang kita lakukan bersifat random, tidak menentu.

Kita baru mencoba menarik data random dari \(N(0,1)\), tapi tentunya kita bisa melakukan langkah yang sama hingga plotting untuk parameter lain, misalnya rata-rata \(\mu=10\) dan standard deviation \(\sigma=8\).

random_normal_2 <- rnorm(n, mean = 10, sd = 8)

hist(random_normal_2,
     main = "Histogram 100 sampel dari N(10,8)")

plot(density(random_normal_2),
     main = "density plot: normal, mean 10, sd 8")

(Pengayaan) Menghampiri distribusi binomial dengan distribusi normal

Misalkan kita membuat bar plot dari \(X \sim \text{Binom}(15, 0.4)\), yaitu distribusi binomial dengan banyaknya percobaan \(n=15\) dan probabilitas sukses \(p=0.4\), misalnya dengan base R,

x_binom <- seq(0, 15, by = 1)
y_binom <- dbinom(x_binom, size = 15, prob = 0.4)
barplot(height = y_binom,
        names.arg = x_binom)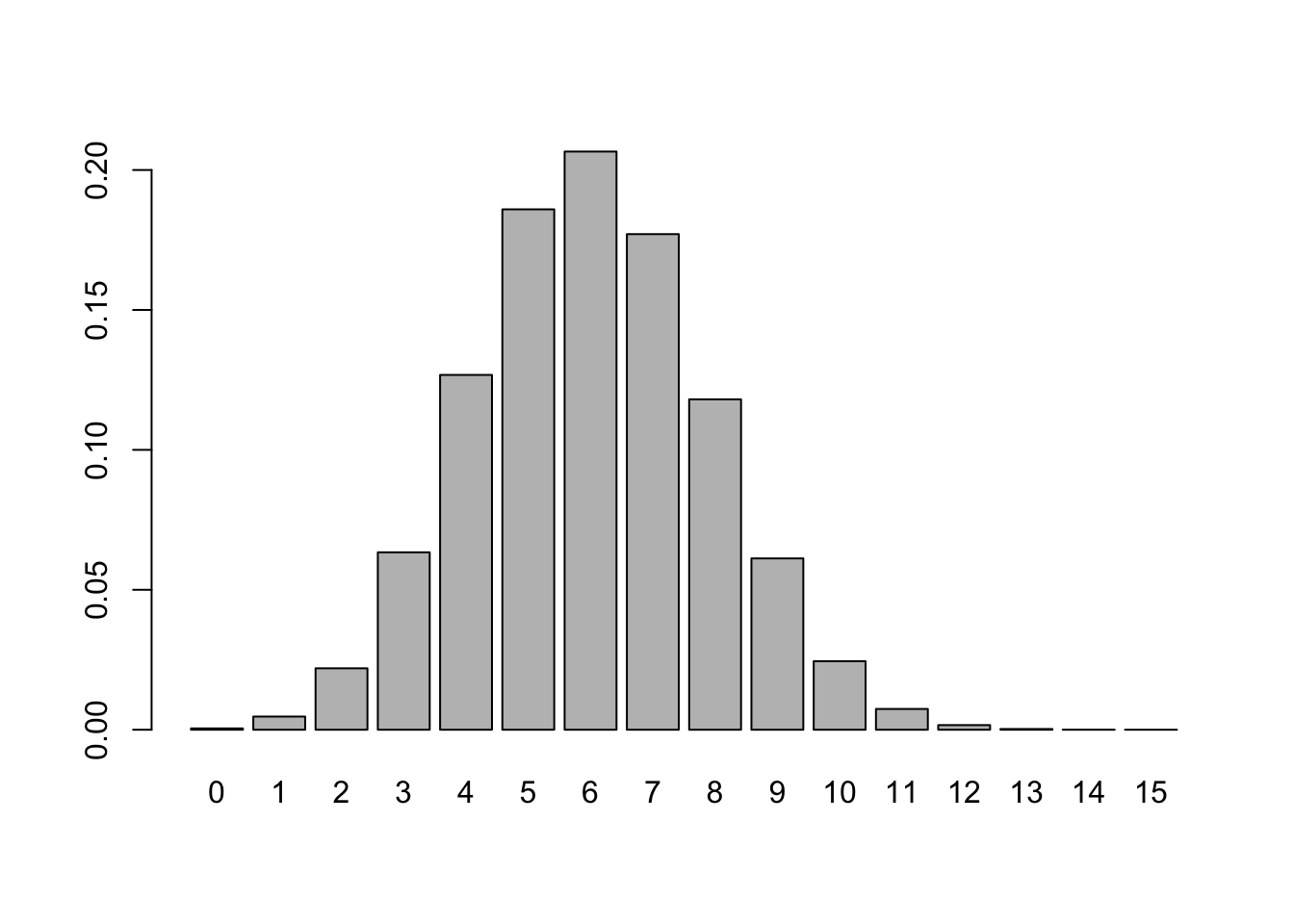

atau dengan ggplot2:

library("ggplot2")

x_binom <- seq(0, 15, by = 1)
y_binom <- dbinom(x_binom, size = 15, prob = 0.4)
df_binom <- data.frame(x = x_binom, Probabilitas = y_binom)

ggplot(df_binom, aes(x = x, y = Probabilitas)) +
  geom_bar(stat = "identity", fill = "blue")

Kemudian, kita bisa menghitung ekspektasi dan standard deviation dari \(X \sim \text{Binom}(15, 0.4)\) yaitu

\[\begin{align*} \text{E}[X] &= np \\ &= (15)(0.4) = 6 \end{align*}\]

\[\begin{align*} \text{Var}[X] &= npq = np(1-q) \\ &= (15)(0.4)(1-0.4) = (15)(0.4)(0.6) \\ &= 3.6 \end{align*}\]

\[\begin{align*} \sigma &= \sqrt{\sigma^2} = \sqrt{\text{Var}[X]} \\ &= \sqrt{3.6} = \frac{3}{5}\sqrt{10} \end{align*}\]

lalu dengan informasi tersebut, kita timpa bar plot binomial dengan plot PDF distribusi normal \(N\left(\mu, \sigma^2\right) = N(6, 3.6)\) sebagai berikut:

x_norm_3 <- seq(0, 15, length = 100) # rentangnya sama dengan x_binom
y_norm_3 <- dnorm(x_norm_3, mean = 6, sd = sqrt(3.6))
df_norm <- data.frame(x = x_norm_3, Densitas = y_norm_3)

ggplot(df_binom, aes(x = x, y = Probabilitas)) +
  geom_bar(stat = "identity", fill = "blue") +
  geom_line(data = df_norm, aes(x = x, y = Densitas))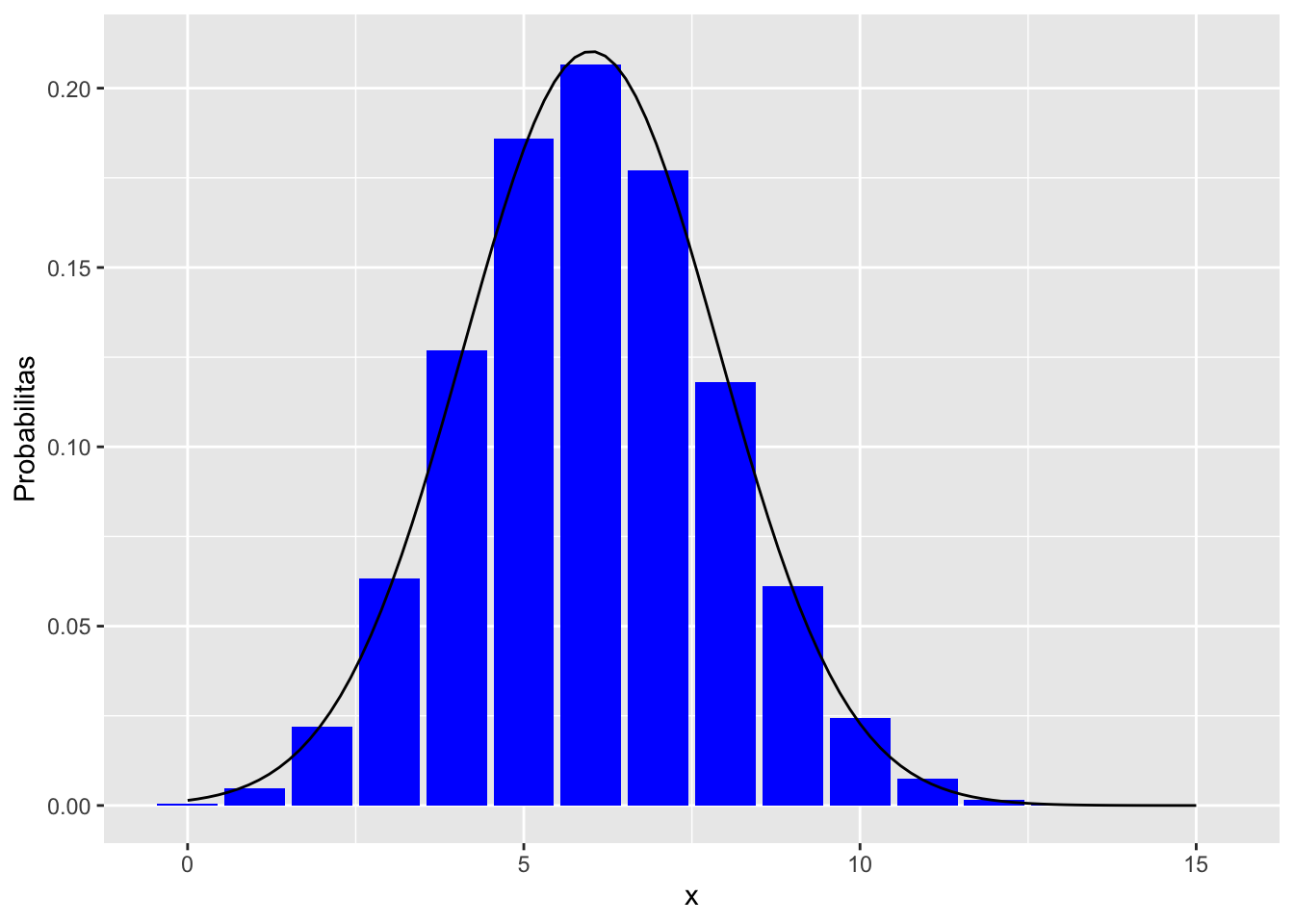

Wah, ternyata sangat mendekati, ya! Distribusi normal bisa digunakan untuk menghampiri distribusi binomial, yaitu

\[\text{Binom}(n,p) \approx \text{N}\left(np,npq\right)\]

dan semakin besar nilai \(n\), semakin akurat.

Distribusi Uniform (Kontinu)

PDF

dunif(40, min = 25, max = 100)

[1] 0.01333333

x_unif <- seq(25-5, 100+5, length = 100)
x_unif

  [1]  20.00000  20.85859  21.71717  22.57576  23.43434  24.29293  25.15152
  [8]  26.01010  26.86869  27.72727  28.58586  29.44444  30.30303  31.16162
 [15]  32.02020  32.87879  33.73737  34.59596  35.45455  36.31313  37.17172
 [22]  38.03030  38.88889  39.74747  40.60606  41.46465  42.32323  43.18182
 [29]  44.04040  44.89899  45.75758  46.61616  47.47475  48.33333  49.19192
 [36]  50.05051  50.90909  51.76768  52.62626  53.48485  54.34343  55.20202
 [43]  56.06061  56.91919  57.77778  58.63636  59.49495  60.35354  61.21212
 [50]  62.07071  62.92929  63.78788  64.64646  65.50505  66.36364  67.22222
 [57]  68.08081  68.93939  69.79798  70.65657  71.51515  72.37374  73.23232
 [64]  74.09091  74.94949  75.80808  76.66667  77.52525  78.38384  79.24242
 [71]  80.10101  80.95960  81.81818  82.67677  83.53535  84.39394  85.25253
 [78]  86.11111  86.96970  87.82828  88.68687  89.54545  90.40404  91.26263
 [85]  92.12121  92.97980  93.83838  94.69697  95.55556  96.41414  97.27273
 [92]  98.13131  98.98990  99.84848 100.70707 101.56566 102.42424 103.28283
 [99] 104.14141 105.00000

plot(x_unif,
     dunif(x_unif, min = 25, max = 100),
     type = 'o')

CDF

punif(40, min = 25, max = 100)

[1] 0.2

Quantile function

qunif(0.2, min = 25, max = 100)

[1] 40

RNG

set.seed(61)
n <- 100
random_unif <- runif(n, min = 25, max = 100)
random_unif

  [1] 51.38044 95.68630 51.53925 26.21991 28.19639 36.83788 72.77575 30.67809
  [9] 31.23775 46.52553 56.89787 44.77957 81.93752 61.58409 77.22397 54.71256
 [17] 93.64523 33.87767 53.17014 54.33197 32.54365 71.72351 30.59663 30.58296
 [25] 76.50455 48.77611 98.08175 82.62318 32.50079 53.21110 29.46335 96.73125
 [33] 73.20886 96.58120 84.05388 84.01955 79.59918 32.49794 38.80875 26.82491
 [41] 66.49560 72.81532 53.80198 63.55768 46.82261 99.53555 87.37795 60.85538
 [49] 68.29078 77.70675 85.03716 48.30345 77.51278 87.68632 47.08067 28.48127
 [57] 49.79398 78.86069 85.10363 30.93439 92.00908 28.60879 31.95021 56.56616
 [65] 70.26537 28.23183 31.97654 78.35911 95.84966 77.07542 41.33189 85.83743
 [73] 97.56560 49.74292 67.42995 87.99055 86.79161 77.93522 36.00223 65.13676
 [81] 48.01646 64.25653 27.53163 68.86392 80.26409 41.29605 67.82670 70.48360
 [89] 91.09336 44.66384 63.81147 63.47403 74.94217 89.52828 41.98855 47.05847
 [97] 51.67670 93.11556 79.55292 78.58793

hist(random_unif)

plot(density(random_unif),
     main = "density plot: uniform, min 25, max 100")

Distribusi Kontinu dengan distr

library("distr")

Loading required package: startupmsg

Utilities for Start-Up Messages (version 0.9.7)

For more information see ?"startupmsg", NEWS("startupmsg")

Loading required package: sfsmisc

Object Oriented Implementation of Distributions (version 2.9.2)

Attention: Arithmetics on distribution objects are understood as operations on corresponding random variables (r.v.s); see distrARITH().
Some functions from package 'stats' are intentionally masked ---see distrMASK().
Note that global options are controlled by distroptions() ---c.f. ?"distroptions".

For more information see ?"distr", NEWS("distr"), as well as
  http://distr.r-forge.r-project.org/
Package "distrDoc" provides a vignette to this package as well as to several extension packages; try vignette("distr").

Attaching package: 'distr'

The following objects are masked from 'package:stats':

    df, qqplot, sd

library("distrEx")

Extensions of Package 'distr' (version 2.9.0)

Note: Packages "e1071", "moments", "fBasics" should be attached /before/ package "distrEx". See distrExMASK().Note: Extreme value distribution functionality has been moved to
      package "RobExtremes". See distrExMOVED().

For more information see ?"distrEx", NEWS("distrEx"), as well as
  http://distr.r-forge.r-project.org/
Package "distrDoc" provides a vignette to this package as well as to several related packages; try vignette("distr").

Attaching package: 'distrEx'

The following objects are masked from 'package:stats':

    IQR, mad, median, var

Distribusi Uniform (Kontinu)

dist1 <- Unif(Min = 25, Max = 100)

plot(dist1)

E(dist1)

[1] 62.5

var(dist1)

[1] 468.75

d(dist1)(40)

[1] 0.01333333

p(dist1)(40)

[1] 0.2

q(dist1)(0.2)

[1] 40

Distribusi Normal

dist2 <- Norm(mean = 0, sd = 1)

plot(dist2)

E(dist2)

[1] 0

var(dist2)

[1] 1

d(dist2)(1.96)

[1] 0.05844094

p(dist2)(1.96)

[1] 0.9750021

q(dist2)(0.975)

[1] 1.959964

Distribusi di Excel

Silakan unduh worksheet berikut untuk bermain di Excel dengan berbagai distribusi, baik diskrit maupun kontinu, yang telah kita bahas, terutama untuk bermain dengan random number generation.

Worksheet versi terbaru: Worksheet Pertemuan 6 (Revisi)

Worksheet versi sebelumnya:

• Worksheet Pertemuan 6

Kita akan memanfaatkan yang namanya “Analysis ToolPak”, juga disebut “XLMiner Analysis ToolPak”. Cara mengaktifkannya tergantung versi Excel, juga tergantung apakah sedang menggunakan Microsoft Excel di desktop atau mengakses secara online.

Mengaktifkan Analysis ToolPak: Microsoft 365 Excel (Web)

Jika kalian menggunakan Excel di versi web Microsoft 365, kalian bisa mencari tombol Add-ins di sisi kanan atas layar kalian (lihat gambar)

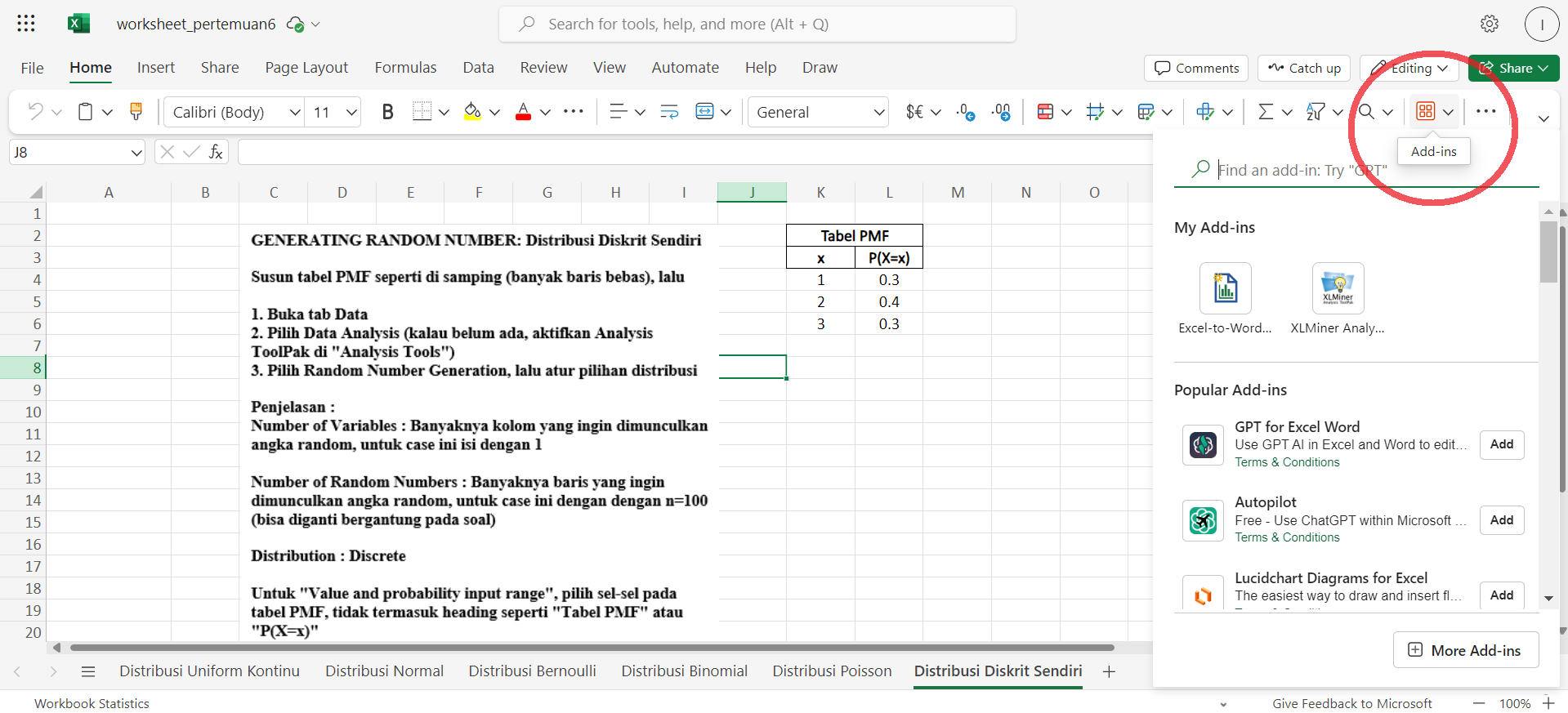
Selanjutnya, kalian bisa ketik “XLMiner Analysis Toolpak” pada search bar

Akan muncul list “Anova: Single Factor”, “Anova: Two Factor” dan lainnya. Langsung saja scroll hingga ditemukan Random Number Generation.

Lalu, ikuti petunjuk yang diberikan di file

Mengaktifkan Analysis ToolPak: Excel 2021

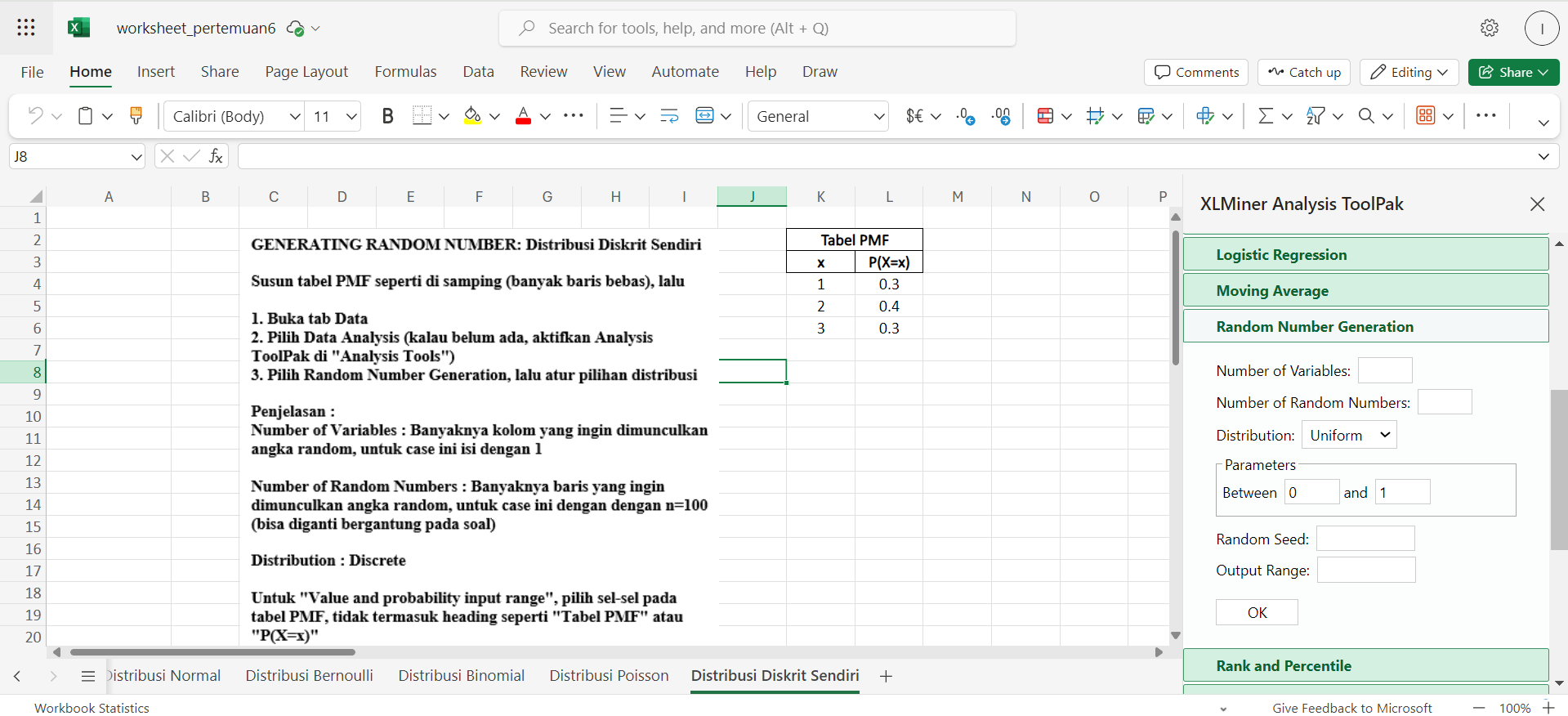
(work in progress)