for (k in 1:5) {
print(k*2)
}[1] 2
[1] 4
[1] 6
[1] 8
[1] 10Sampling Distributions in R
November 4, 2024
Kembali ke Pengantar Sains Data
Kebetulan, materi modul kali ini adalah revisi dari modul PSD tahun lalu.
Dalam menganalisis suatu populasi secara statistik, apabila populasinya tidak kecil, realitanya kita tidak bisa memperoleh data yang benar-benar lengkap tentang keseluruhan populasi tersebut. Kita hanya bisa mengambil sampel, yaitu subset dari populasi. Sampel yang kita ambil diharapkan cukup “mewakili” data populasi, yaitu nilai-nilai statistiknya (baik ukuran pemusatan data, seperti rata-rata, maupun ukuran persebaran/keragaman data, seperti variansi) tidak berbeda jauh.
(Metode-metode pengambilan sampel dengan baik dipelajari di mata kuliah Sampling dan Rancangan Survey.)
Maksud istilah “statistik” di sini adalah perhitungan yang bisa dilakukan pada sembarang sampel. Misalnya, sampel apapun bisa dihitung rata-ratanya ataupun variansinya, sehingga rata-rata dan variansi termasuk statistik. Perhatikan bahwa “sampel” berupa sekumpulan data, bukan satu titik data saja.
Nilai statistik bergantung pada sampel. Dengan demikian, statistik bisa dipandang sebagai variabel acak, sehingga memiliki distribusi. Distribusi dari suatu statistik disebut sampling distribution atau distribusi sampling.
Contoh: distribusi dari rata-rata disebut distribusi sample mean.
Sebagaimana distribusi pada umumnya, distribusi sampling sebenarnya menggambarkan probabilitas memperoleh nilai statistik tertentu. Misalnya, distribusi sample mean menggambarkan probabilitas memperoleh nilai rata-rata tertentu dari sampel yang kebetulan kita miliki.
Dengan demikian, sejatinya, kita bisa membentuk distribusi sampling dengan mencoba semua kemungkinan sampel serta mendata probabilitas memperoleh tiap sampel tersebut, kemudian menghitung statistiknya untuk tiap sampel, barulah mendata semua nilai yang mungkin untuk statistik tersebut beserta probabilitasnya.
Namun, karena ada amat sangat banyak kemungkinan sampel, seringkali kita malah memperkirakan bentuk distribusi sampling tersebut melalui simulasi, yaitu mencoba mengambil sampel berkali-kali secara random, kemudian menghitung statistiknya di tiap sampel, barulah membentuk distribusi dari statistik tersebut.
Bagaimanapun juga, ketika membahas distribusi sampling, yang melibatkan pengambilan sampel hingga berkali-kali, tentu ada semacam konsep pengulangan.
Jangan lupa bahwa R adalah bahasa pemrograman, sehingga juga memiliki fitur pernyataan berulang, sebagaimana yang kalian pelajari di mata kuliah Algoritma dan Pemrograman, seperti di Python yang kalian pelajari di mata kuliah Praktikum Algoritma dan Pemrograman. Sebelum mempelajari distribusi sampling di R, kita perlu membahas itu dulu.
replicateSintaks/penulisan kode seperti di bawah ini, yaitu dengan fungsi replicate, hanya berlaku di bahasa pemrograman R.
Jangan gunakan replicate di mata kuliah Algoritma dan Pemrograman!
Mengeksekusi ulang fungsi/perintah yang diberikan, sebanyak yang kita minta, tanpa harus membuat for loop
(work in progress)
Untuk mempermudah urusan distribusi, mari kita aktifkan package distr dan distrEx yang sudah kita kenal sebelumnya
Loading required package: startupmsgUtilities for Start-Up Messages (version 0.9.7)For more information see ?"startupmsg", NEWS("startupmsg")Loading required package: sfsmiscObject Oriented Implementation of Distributions (version 2.9.2)Attention: Arithmetics on distribution objects are understood as operations on corresponding random variables (r.v.s); see distrARITH().
Some functions from package 'stats' are intentionally masked ---see distrMASK().
Note that global options are controlled by distroptions() ---c.f. ?"distroptions".For more information see ?"distr", NEWS("distr"), as well as
http://distr.r-forge.r-project.org/
Package "distrDoc" provides a vignette to this package as well as to several extension packages; try vignette("distr").
Attaching package: 'distr'The following objects are masked from 'package:stats':
df, qqplot, sdExtensions of Package 'distr' (version 2.9.0)Note: Packages "e1071", "moments", "fBasics" should be attached /before/ package "distrEx". See distrExMASK().Note: Extreme value distribution functionality has been moved to
package "RobExtremes". See distrExMOVED().For more information see ?"distrEx", NEWS("distrEx"), as well as
http://distr.r-forge.r-project.org/
Package "distrDoc" provides a vignette to this package as well as to several related packages; try vignette("distr").
Attaching package: 'distrEx'The following objects are masked from 'package:stats':
IQR, mad, median, varMisalkan kita punya suatu populasi seperti berikut
Kita bisa saja membentuk distribusi dari populasi tersebut, dengan pertama membuat tabel frekuensi,
Kemudian membagi tiap nilai di tabelnya dengan total frekuensi, agar memperoleh tabel probabilitas (yang menjadi tabel PMF):
popu1
1 2 3 4 5 6 7 8
0.125 0.125 0.125 0.125 0.125 0.125 0.125 0.125 Kita bisa peroleh baris pertama (nilai-nilai yang mungkin),
Sehingga kita bisa membentuk distribusi populasi tersebut dengan distr seperti berikut:
Kita bisa peroleh kembali support dan sebaran probabilitasnya seperti berikut
Kita bisa melihat sebarannya:
Sekarang, mari kita coba mengambil berbagai ukuran sampel dari populasi tersebut, dengan pengembalian. Secara pemrograman, kita bisa langsung mengambil sampel dari popu1, atau bisa juga mengambil sampel dari distribusi dist1 yang bersesuaian. Pengambilan sampel yang berkali-kali itu bisa dilakukan dengan for loop ataupun dengan fungsi replicate
replicate, dari populasireplicate, dari distribusiSample size 3, 1000 kali percobaan
sample_means <-
replicate(
1000,
mean(
sample(x = popu1,
size = 3,
replace = TRUE)))
hist(sample_means,
main = "Sample Size of 3",
xlab = "Sample Means")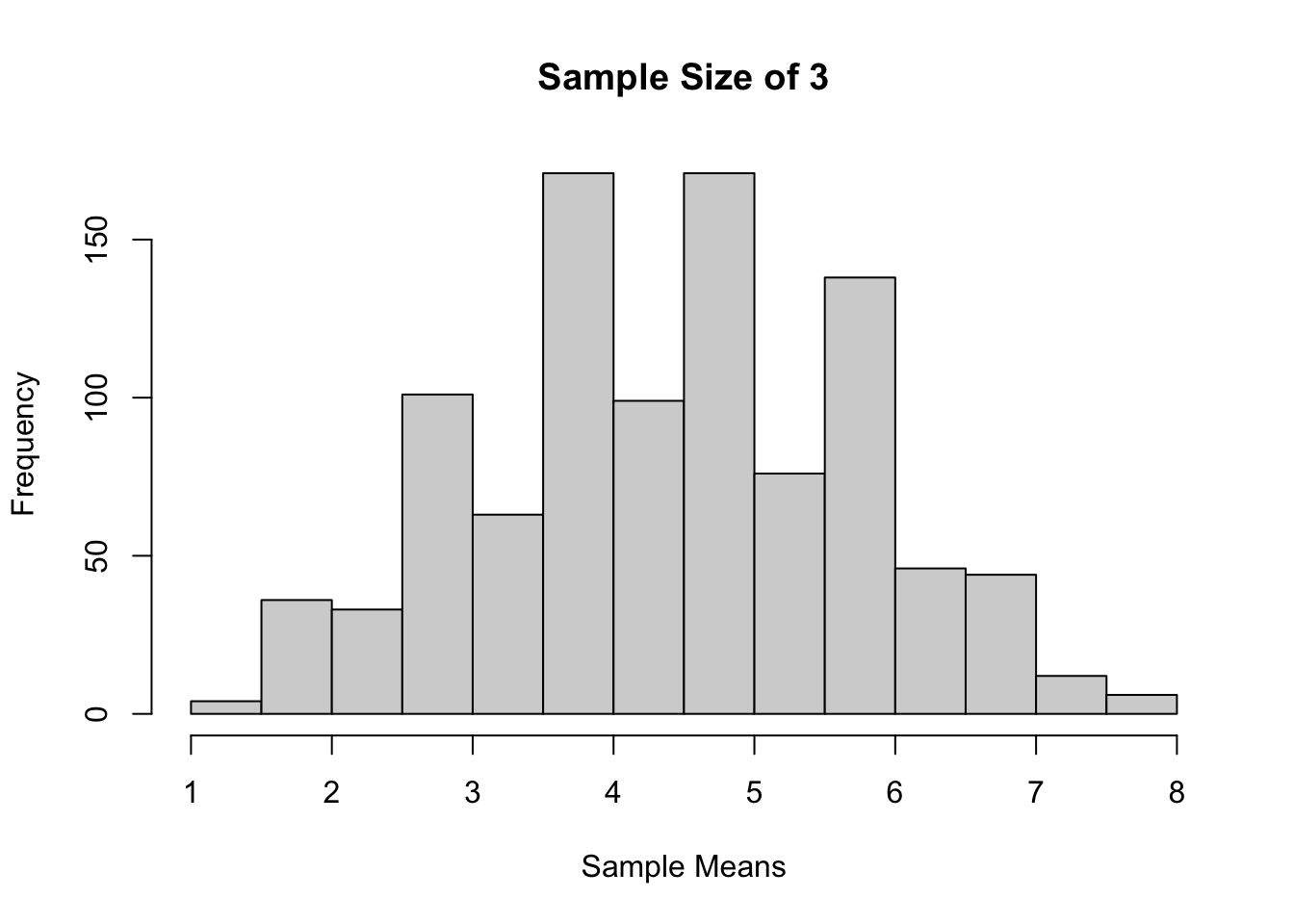
Sample size 10, 1000 kali percobaan
sample_means <-
replicate(
1000,
mean(
sample(x = popu1,
size = 10,
replace = TRUE)))
hist(sample_means,
main = "Sample Size of 10",
xlab = "Sample Means")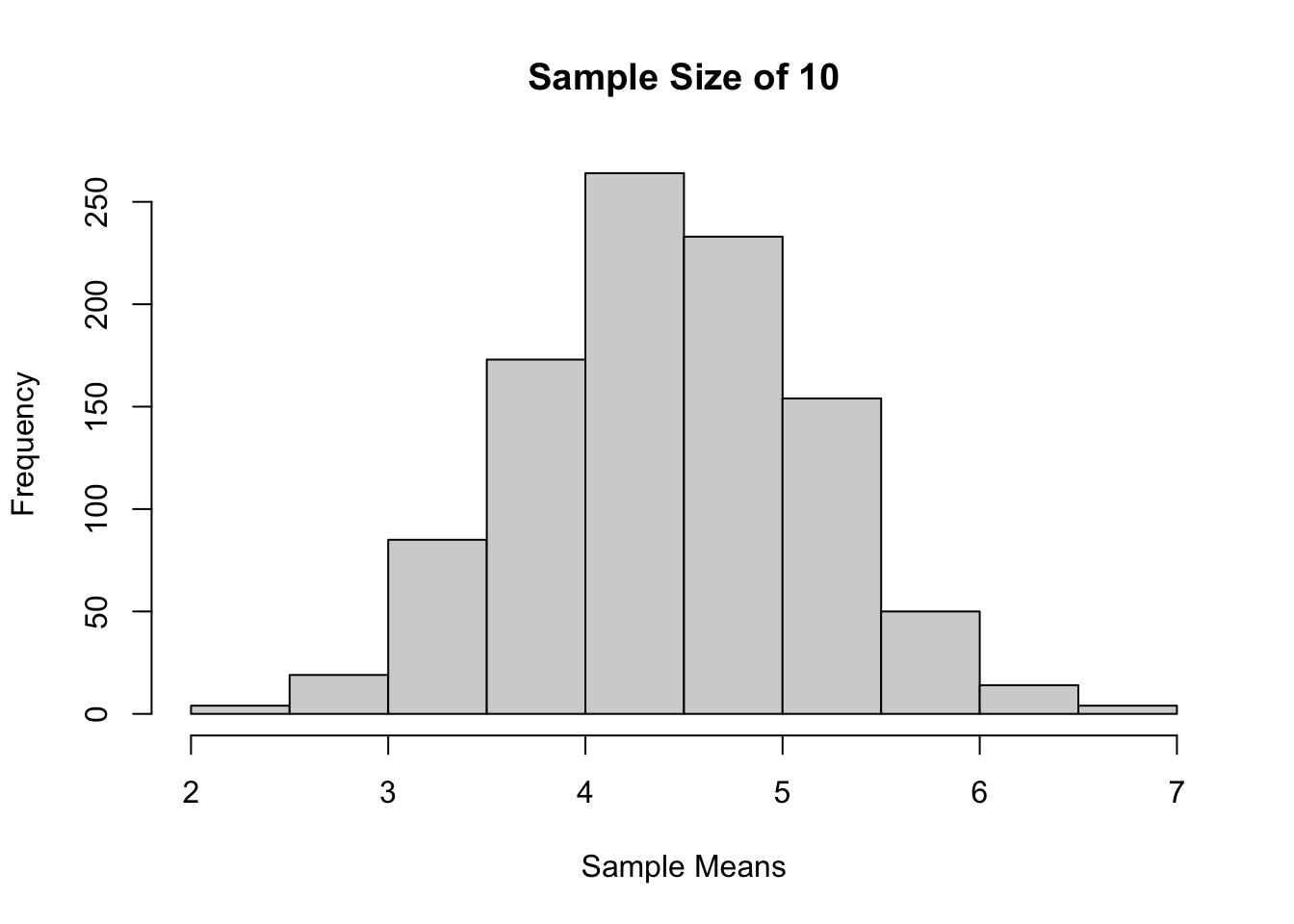
Sample size 50, 1000 kali percobaan
Sample size 3, 1000 kali percobaan
sample_means <-
replicate(
1000,
mean(
sample(x = support(dist1),
prob = prob(dist1),
size = 3,
replace = TRUE)))
hist(sample_means,
main = "Sample Size of 3",
xlab = "Sample Means")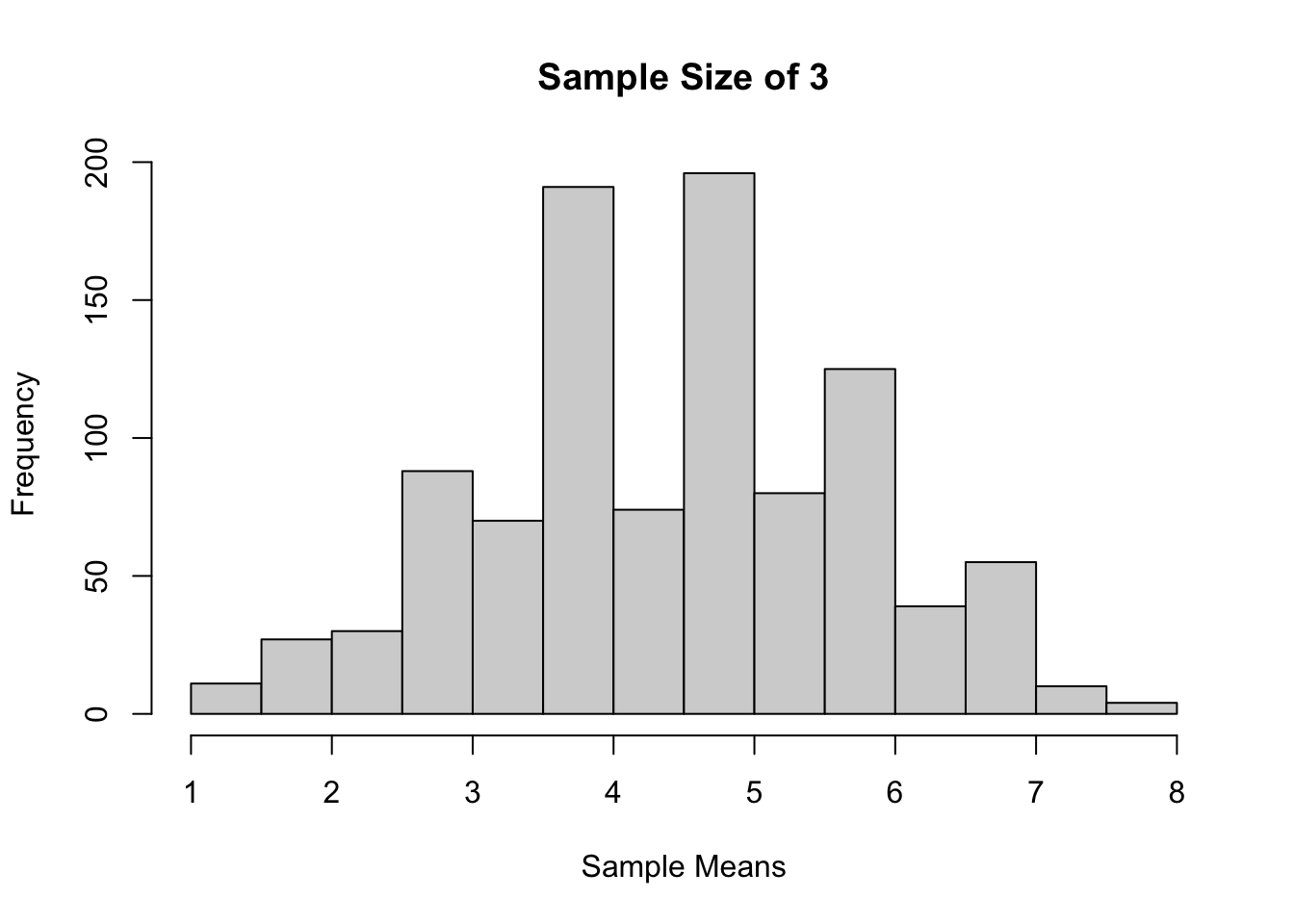
Sample size 10, 1000 kali percobaan
sample_means <-
replicate(
1000,
mean(
sample(x = support(dist1),
prob = prob(dist1),
size = 10,
replace = TRUE)))
hist(sample_means,
main = "Sample Size of 10",
xlab = "Sample Means")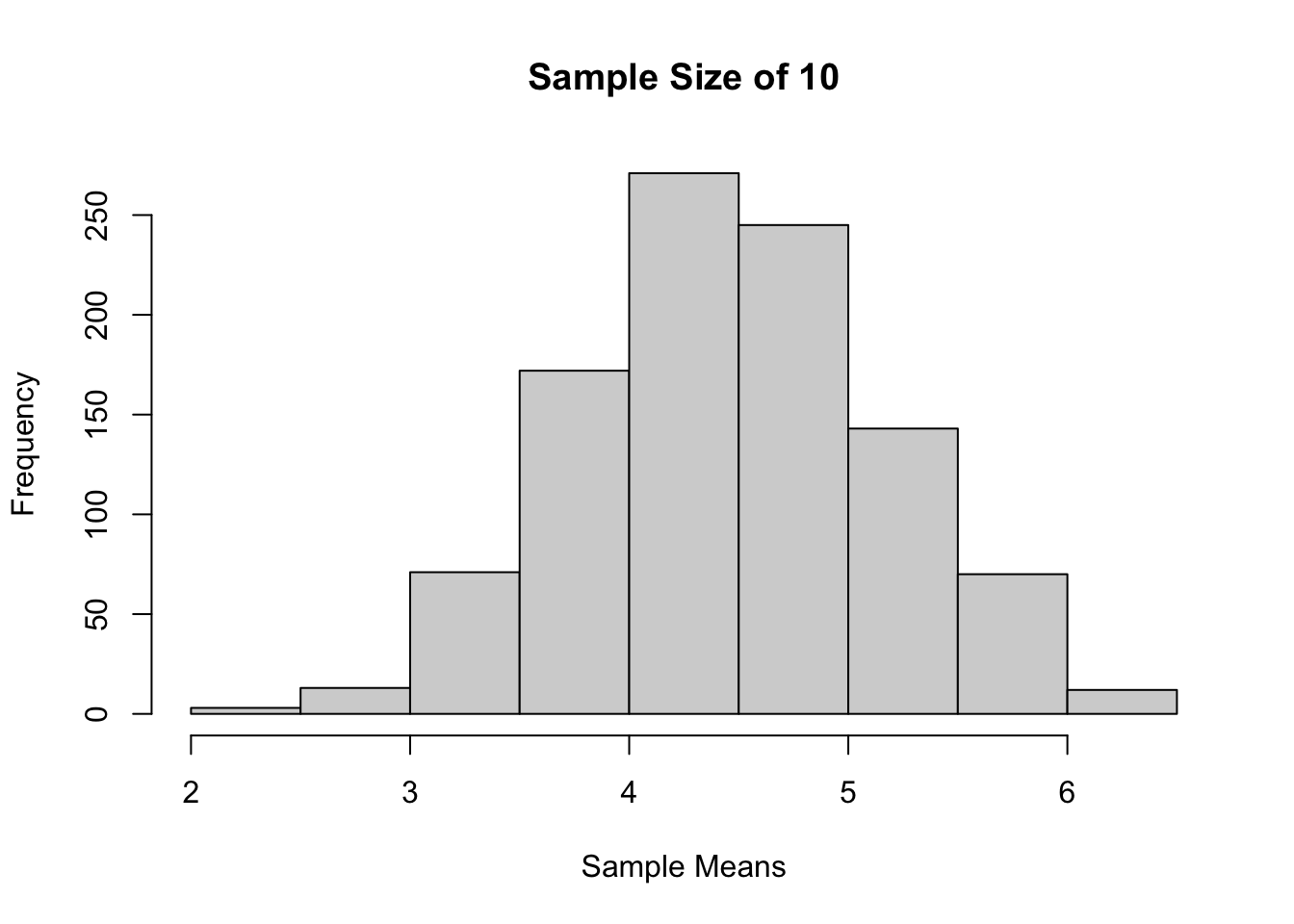
Sample size 50, 1000 kali percobaan
Sample size 3, 1000 kali percobaan
sample_means <- c( )
for (i in 1:1000) {
sample_means[i] <-
mean(
sample(x = popu1,
size = 3,
replace = TRUE))
}
hist(sample_means,
main = "Sample Size of 3",
xlab = "Sample Means")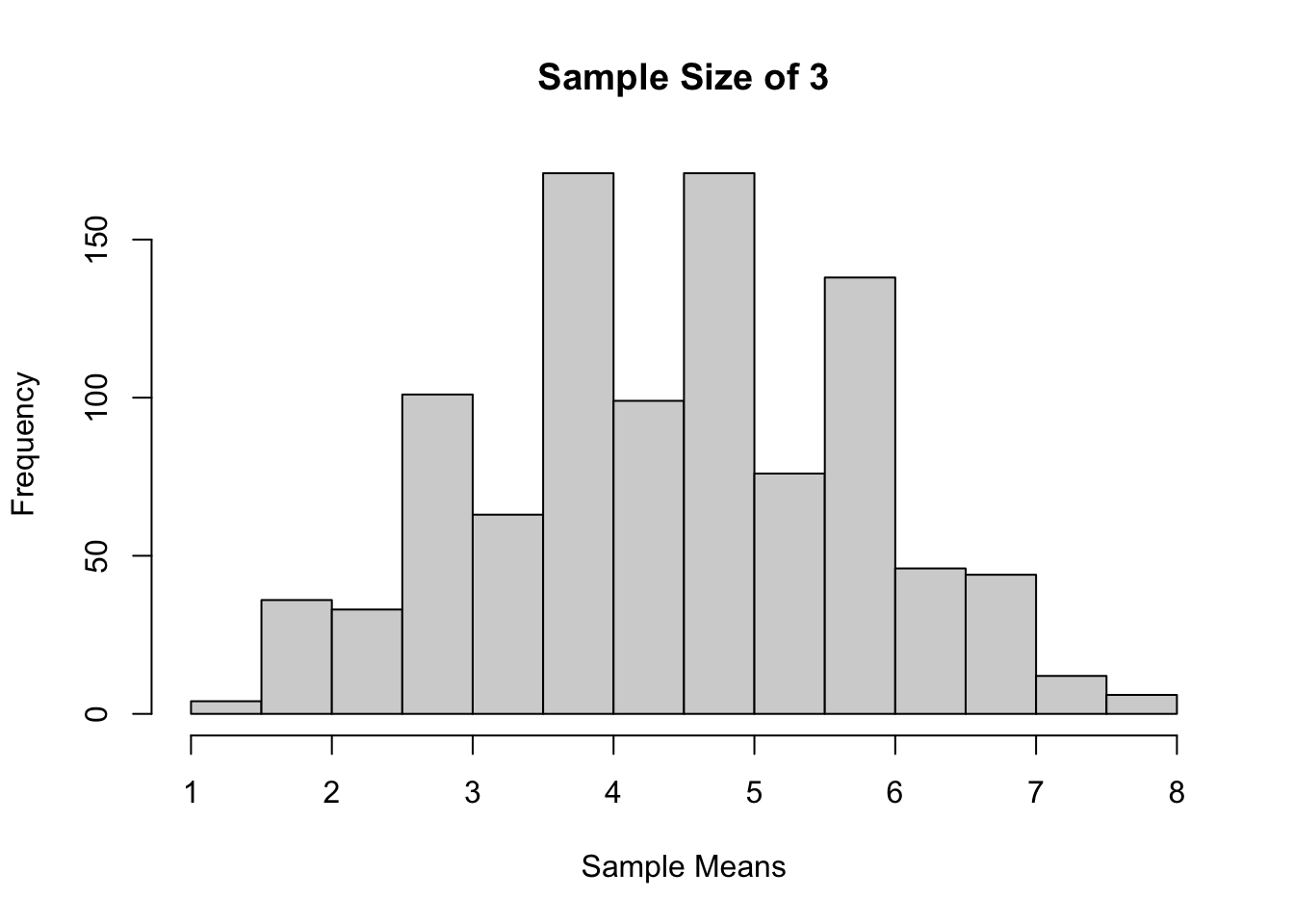
Sample size 10, 1000 kali percobaan
sample_means <- c( )
for (i in 1:1000) {
sample_means[i] <-
mean(
sample(x = popu1,
size = 10,
replace = TRUE))
}
hist(sample_means,
main = "Sample Size of 10",
xlab = "Sample Means")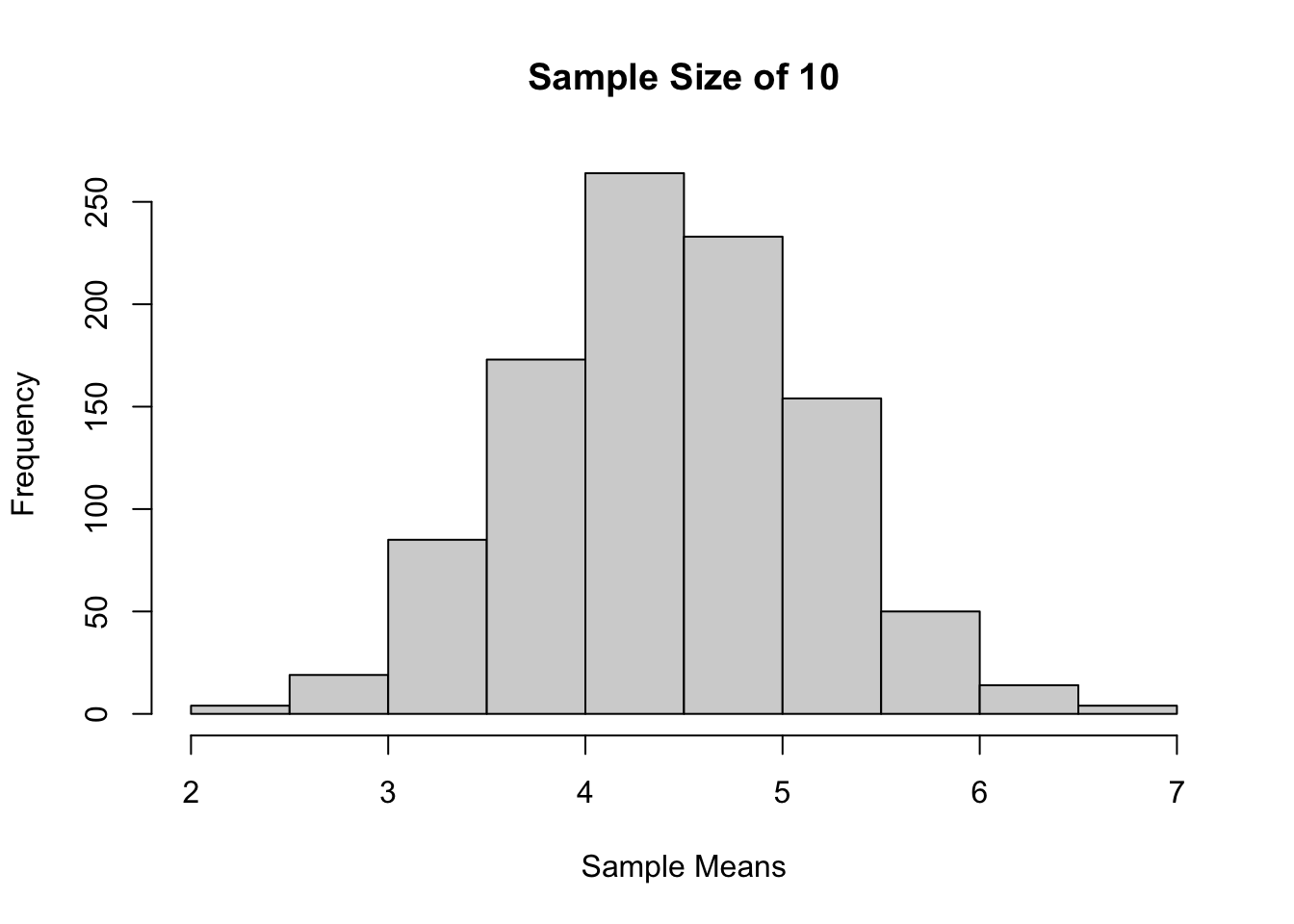
Sample size 50, 1000 kali percobaan
Sample size 3, 1000 kali percobaan
sample_means <- c( )
for (i in 1:1000) {
sample_means[i] <-
mean(
sample(x = support(dist1),
prob = prob(dist1),
size = 3,
replace = TRUE))
}
hist(sample_means,
main = "Sample Size of 3",
xlab = "Sample Means")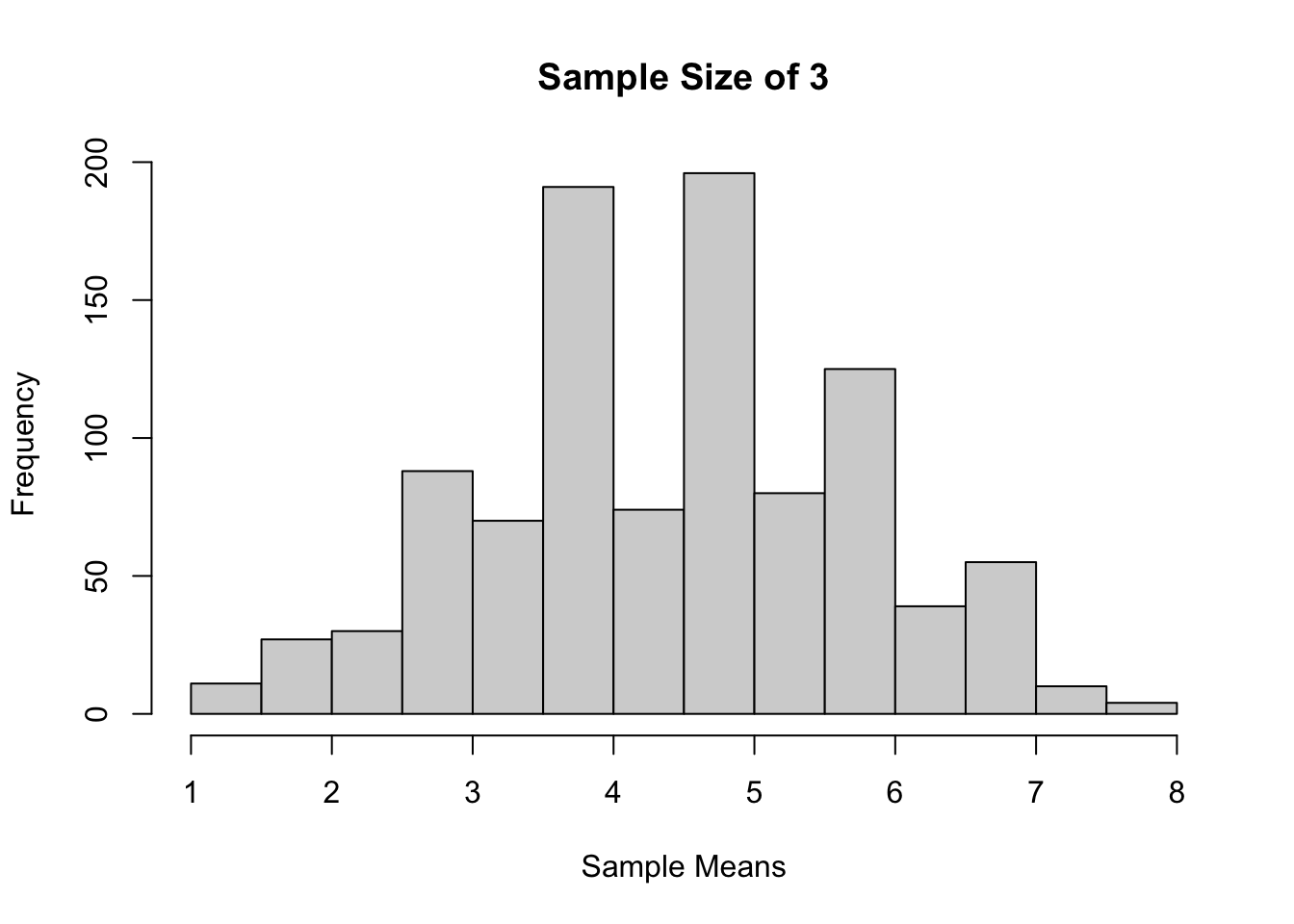
Sample size 10, 1000 kali percobaan
sample_means <- c( )
for (i in 1:1000) {
sample_means[i] <-
mean(
sample(x = support(dist1),
prob = prob(dist1),
size = 10,
replace = TRUE))
}
hist(sample_means,
main = "Sample Size of 10",
xlab = "Sample Means")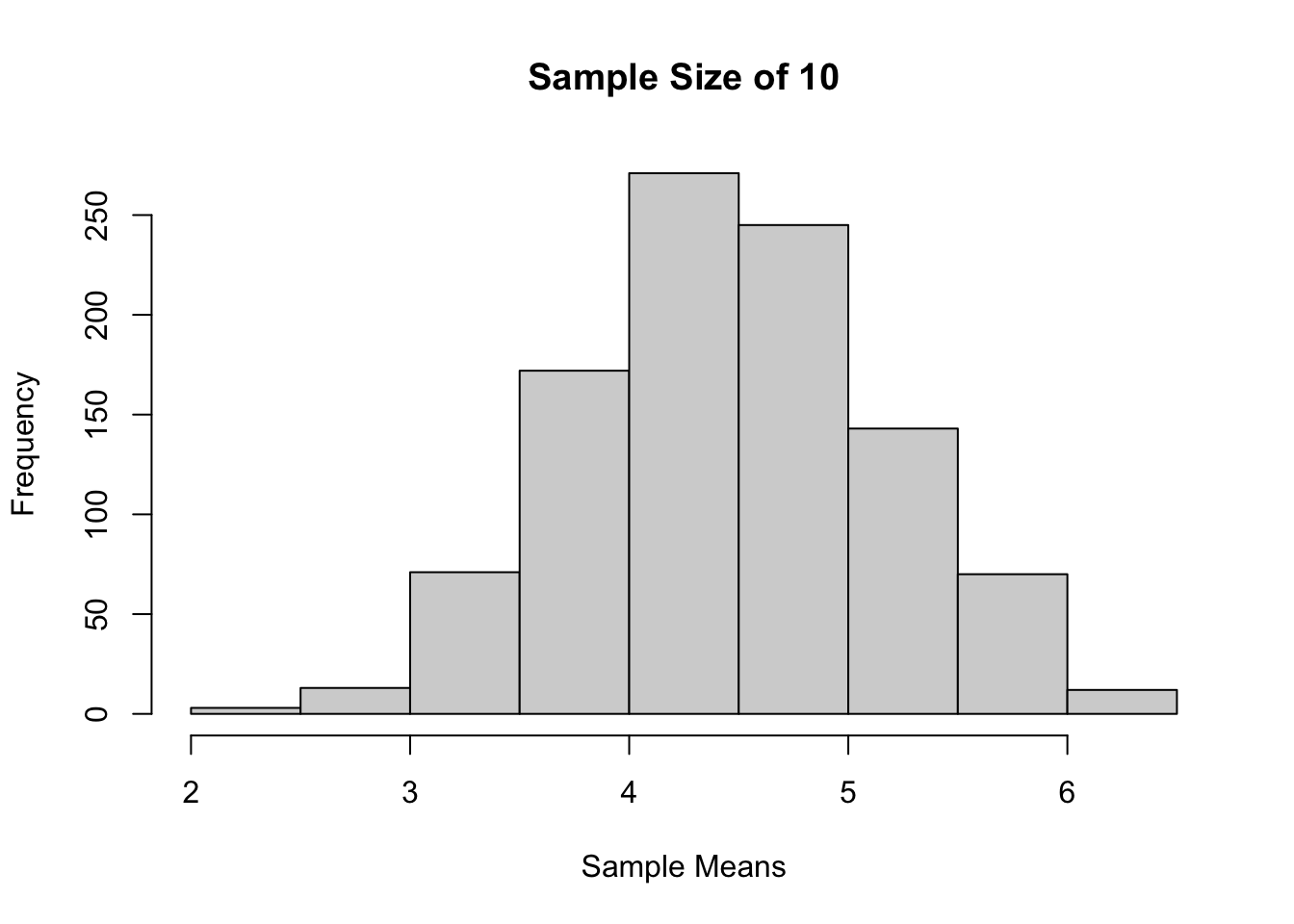
Sample size 50, 1000 kali percobaan
Jika dilihat berdasarkan histogram dari ketiga sampling tadi, bisa terlihat bahwa semakin besar ukuran sampelnya, maka distribusi sample mean akan semakin mendekati distribusi normal
Daripada melakukan simulasi yang mengandalkan random, untuk ukuran sampel yang cukup kecil, kita bisa saja melihat semua kemungkinan pengambilan sampel, menghitung statistiknya (misalnya di sini statistik rata-rata), lalu menghitung probabilitasnya, untuk memperoleh distribusi sampling untuk statistik tersebut (misalnya di sini distribusi sample mean) secara eksak.
Kita akan meninjau semua kemungkinan pengambilan dua sampel dengan pengembalian. Untuk itu, kita memerlukan package gtools yang menyediakan fungsi-fungsi kombinatorik seperti permutations dan combinations untuk memperoleh semua kemungkinan seperti itu
install.packages("gtools")Mari kita coba untuk populasi yang berdistribusi diskrit berhingga. Distribusi tersebut bisa kita buat sendiri, misalnya sebagai berikut:
supp2 <- c(0, 1, 2, 3)
prob2 <- c(1/4, 1/4, 1/4, 1/4)
dist2 <- DiscreteDistribution(supp = supp2,
prob = prob2)
plot(dist2)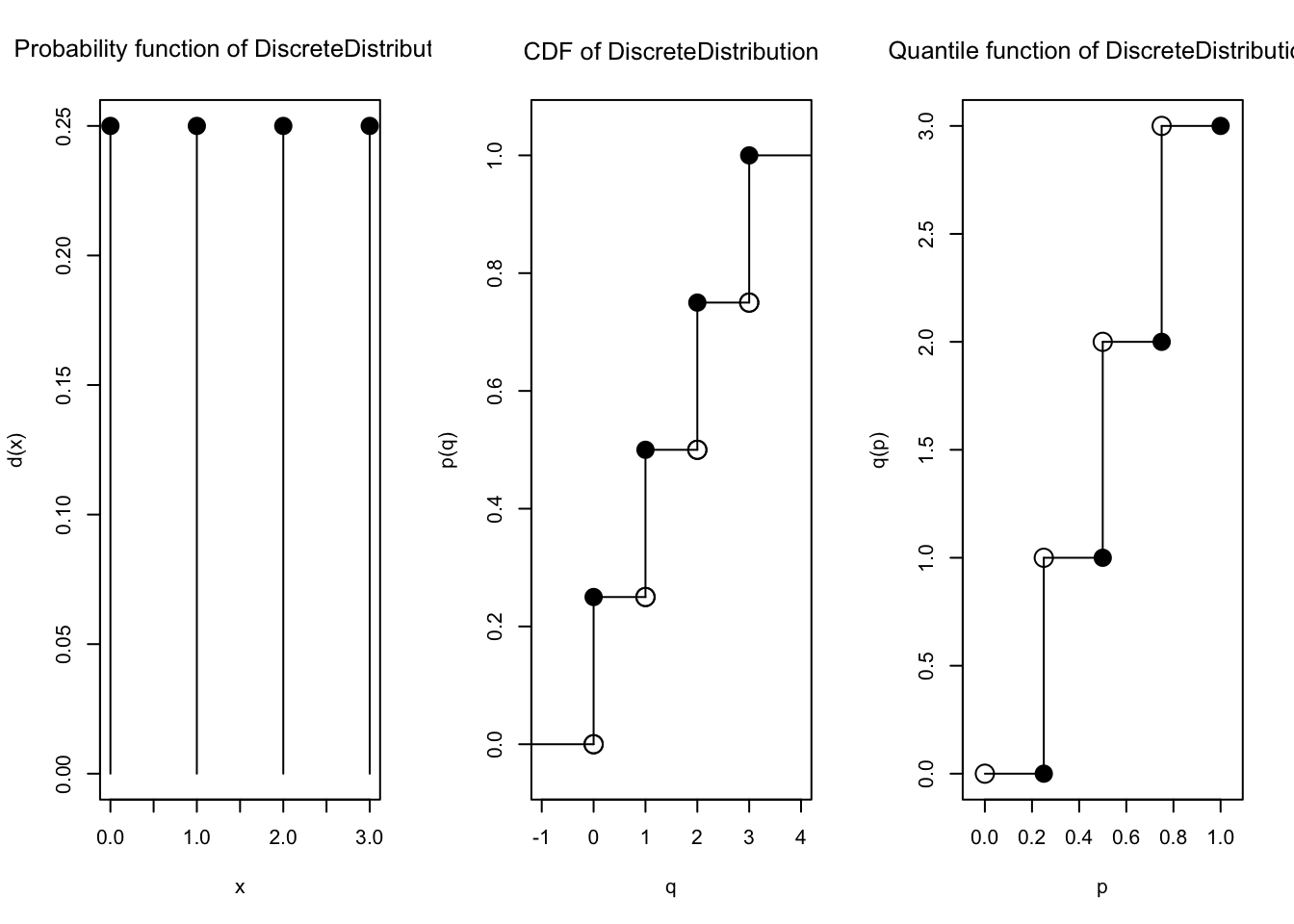
(Sebenarnya dist2 ini juga bisa berupa distribusi Bernoulli, binomial, ataupun distribusi diskrit lainnya.)
Kita bisa menghasilkan semua kemungkinan sampel berukuran 2 dengan pengembalian, menggunakan fungsi permutations dari package gtools, sebagai berikut:
mat2 <- permutations(n = length(support(dist2)),
r = 2, # ukuran sampel
v = support(dist2),
repeats.allowed = TRUE)
mat2 [,1] [,2]
[1,] 0 0
[2,] 0 1
[3,] 0 2
[4,] 0 3
[5,] 1 0
[6,] 1 1
[7,] 1 2
[8,] 1 3
[9,] 2 0
[10,] 2 1
[11,] 2 2
[12,] 2 3
[13,] 3 0
[14,] 3 1
[15,] 3 2
[16,] 3 3Hasilnya berupa matriks, yang bisa kita ubah jadi data frame,
X1 X2
1 0 0
2 0 1
3 0 2
4 0 3
5 1 0
6 1 1
7 1 2
8 1 3
9 2 0
10 2 1
11 2 2
12 2 3
13 3 0
14 3 1
15 3 2
16 3 3Kemudian, kita ingin menghitung rata-rata dari tiap kemungkinan dua sampel. Kita bisa apply atau menerapkan fungsi statistik yang kita inginkan, misalnya mean atau rata-rata, untuk tiap baris di matriks mat2, sebagai berikut
Hasilnya bisa kita simpan sebagai kolom baru di data frame, misal kolom Xbar
X1 X2 Xbar
1 0 0 0.0
2 0 1 0.5
3 0 2 1.0
4 0 3 1.5
5 1 0 0.5
6 1 1 1.0
7 1 2 1.5
8 1 3 2.0
9 2 0 1.0
10 2 1 1.5
11 2 2 2.0
12 2 3 2.5
13 3 0 1.5
14 3 1 2.0
15 3 2 2.5
16 3 3 3.0Sekarang, df_perm2 menyimpan semua kemungkinan sampel berukuran 2 dengan pengembalian yang mungkin, disertai rata-rata masing-masing.
Selanjutnya, kita perlu menghitung probabilitas dari tiap kemungkinan sampel. Perhatikan bahwa, karena sampling dilakukan dengan pengembalian, probabilitas antar tiap pengambilan bersifat independen. Sehingga, kita tinggal mengalikan probabilitas untuk masing-masing pengambilan.
Caranya, kita bisa menghitung probabilitas masing-masing pengambilan (membuat matriks baru, misal mat2_prob), baru melakukan perkalian per baris.
Karena distribusi dist2 tergolong diskrit, kita bisa menerapkan PMFnya yaitu fungsi d
[1] 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25
[16] 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25
[31] 0.25 0.25Waduh, hasilnya malah flat, daripada berbentuk matriks. Agar tetap berbentuk matriks, kita gunakan fungsi apply lagi, sebagai berikut
[,1] [,2]
[1,] 0.25 0.25
[2,] 0.25 0.25
[3,] 0.25 0.25
[4,] 0.25 0.25
[5,] 0.25 0.25
[6,] 0.25 0.25
[7,] 0.25 0.25
[8,] 0.25 0.25
[9,] 0.25 0.25
[10,] 0.25 0.25
[11,] 0.25 0.25
[12,] 0.25 0.25
[13,] 0.25 0.25
[14,] 0.25 0.25
[15,] 0.25 0.25
[16,] 0.25 0.25Sekarang kita tinggal mengalikan tiap baris (dengan apply lagi), dan menyimpan hasilnya sebagai kolom baru di data frame, misal prob
X1 X2 Xbar prob
1 0 0 0.0 0.0625
2 0 1 0.5 0.0625
3 0 2 1.0 0.0625
4 0 3 1.5 0.0625
5 1 0 0.5 0.0625
6 1 1 1.0 0.0625
7 1 2 1.5 0.0625
8 1 3 2.0 0.0625
9 2 0 1.0 0.0625
10 2 1 1.5 0.0625
11 2 2 2.0 0.0625
12 2 3 2.5 0.0625
13 3 0 1.5 0.0625
14 3 1 2.0 0.0625
15 3 2 2.5 0.0625
16 3 3 3.0 0.0625Kini, tiap kemungkinan sampel berukuran 2 dengan pengembalian sudah disertai rata-rata dan probabilitas. Untuk memperoleh tabel (PMF untuk) distribusi sample mean, kita tinggal melakukan “pengelompokkan” data untuk tiap nilai statistiknya yaitu Xbar atau rata-rata, sembari menjumlahkan probabilitas. Caranya bisa dengan kode seperti berikut
Xbar prob
1 0.0 0.0625
2 0.5 0.1250
3 1.0 0.1875
4 1.5 0.2500
5 2.0 0.1875
6 2.5 0.1250
7 3.0 0.0625Xbar_prob2 adalah tabel PMF dari sample mean, yang telah diperoleh secara eksak. Mari kita visualisasikan distribusi sample mean tersebut menggunakan histogram, tetapi dengan fungsi barplot agar tiap nilai rata-rata memiliki bar tersendiri
barplot(height = Xbar_prob2[["prob"]],
names.arg = Xbar_prob2[["Xbar"]],
ylim = c(0, 5/16),
yaxp = c(0, 5/16, 5))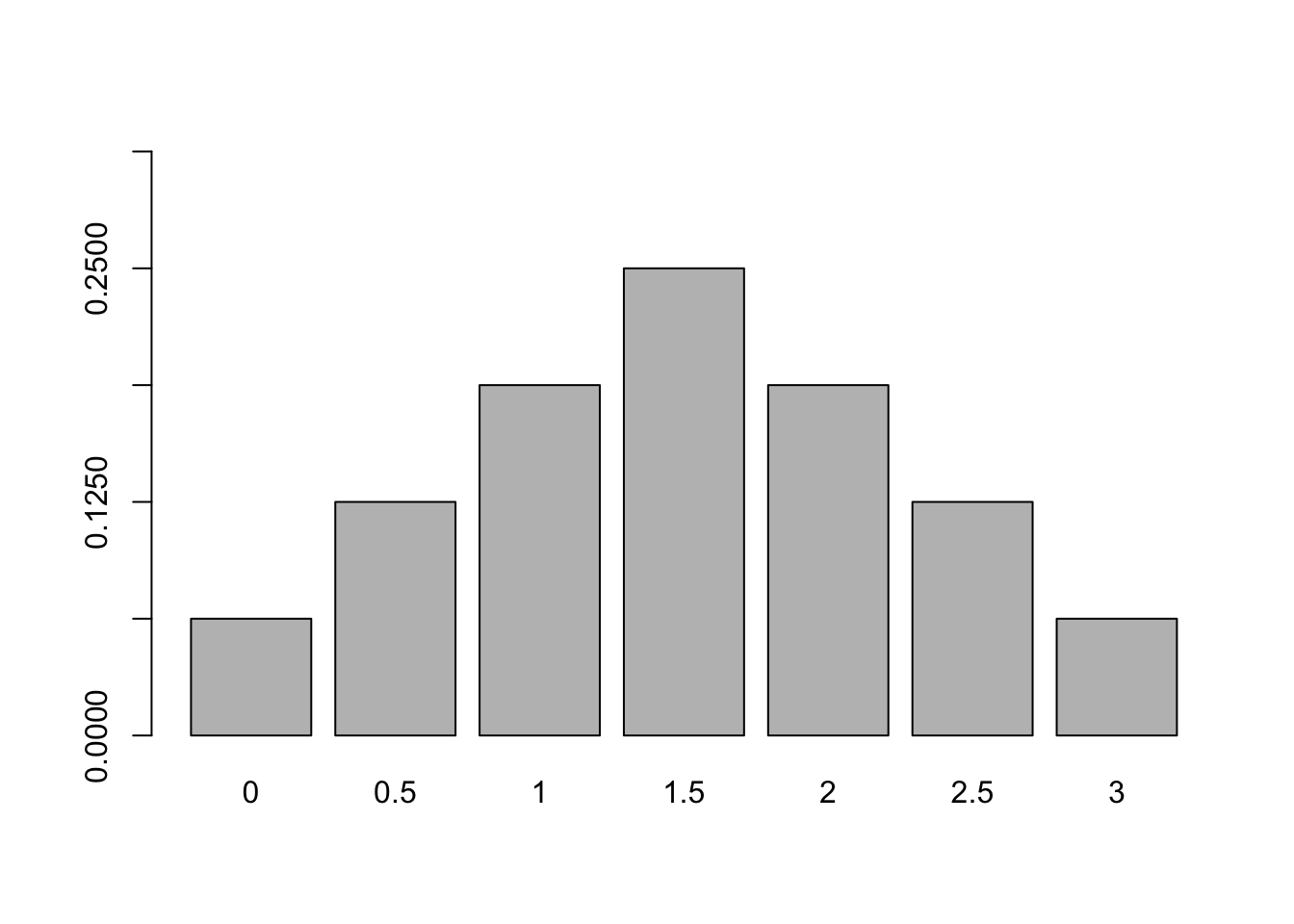
Oh iya, karena sample mean berupa distribusi, kita juga bisa menggunakan distr lagi untuk membentuk distribusinya (karena kita sudah punya tabel PMFnya).
mean_dist2 <-
DiscreteDistribution(supp = Xbar_prob2[["Xbar"]],
prob = Xbar_prob2[["prob"]])
prob(mean_dist2) 0 0.5 1 1.5 2 2.5 3
0.0625 0.1250 0.1875 0.2500 0.1875 0.1250 0.0625 Sehingga, kita bisa menghitung ekspektasi dan variansinya serta membuat plot, seperti berikut.
Whew! Perhatikan bahwa, untuk sampel berukuran 2, ternyata kemungkinannya cukup banyak. Lihat kembali dimensi dari mat2 yaitu matriks berisi semua kemungkinan sampel berukuran 2 dengan pengembalian:
Banyaknya baris bisa sampai 16 ini dihasilkan dari rumus banyaknya permutasi dengan pengulangan (permutations with repitition), yaitu
\[n^r = 4^2 = 16\]
Dengan 4 adalah ukuran support di distribusi asalnya, dan 2 adalah ukuran sampel. Ini masih contoh kecil.
Bayangkan apabila ukuran sampelnya besar. Maka banyaknya kemungkinan pengambilan menjadi amat sangat banyak. Terlalu banyak, sehingga lebih baik kita lakukan suatu penghampiran daripada langsung menghitung distribusi sample mean secara eksak.
Untuk itu, perhatikan dalil-dalil berikut.
Dalil 1
Apabila sampel acak berukuran \(n\) diambil dengan pengembalian dari populasi berhingga yang berukuran \(N\), dimana populasi tersebut mempunyai mean \(\mu\) dan variansi \(\sigma^2\) , maka untuk \(n\) yang besar, distribusi dari sample mean \(\bar{X}\) akan mendekati distribusi normal \(N\left(\mu_{\bar{X}}, \sigma_{\bar{X}}^2\right)\) dengan mean dan variansi berikut:
\[\mu_{\bar{X}} = \mu\]
\[\sigma_{\bar{X}}^2 = \frac{\sigma^2}{n}\]
Dengan demikian,
\[Z = \frac{\bar{X} - \mu}{\left(\frac{\sigma}{\sqrt{n}}\right)} \; \text{mendekati} \; N(0,1)\]
Catatan: Dalil 1 berlaku untuk populasi berhingga dengan ukuran sampel \(\mathbf{n \geq 30}\). Dalil 1 berlaku untuk \(n < 30\) apabila distribusi dari populasinya tidak terlalu menyimpang dari distribusi normal.
Contoh
Misalkan diberikan populasi 1,1,1,3,4,5,6,6,6,7 dan misalkan diambil sampel acak berukuran 36 dari populasi tersebut dengan pengembalian. Tentukan probabilitas bahwa nilai rata-rata sampelnya antara 3.85 dan 4.45 !
Jawab:
Sebut saja populasi yang diberikan berdistribusi \(X\). Distribusi sample mean yang bersesuaian dilambangkan \(\bar{X}\). Soal meminta
\[\text{Pr}\left(3.85 < \bar{X} < 4.45\right)\]
Kita akan menghampiri distribusi \(\bar{X}\) dengan suatu distribusi normal, sesuai yang ditentukan oleh Dalil 1. Kita definisikan dulu populasinya:
Misal \(n\) adalah ukuran sampel
Kita hitung statistik dari populasinya
Variansi adalah kuadrat dari standard deviation
Memanfaatkan Dalil 1, kita bisa anggap rata-rata populasi \(\mu\) sebagai rata-rata dari suatu distribusi normal, dan variansi populasi \(\sigma^2\) yang kemudian dibagi \(n\) menghasilkan variansi dari distribusi normal tersebut, yang akan dihampiri oleh (ataupun menghampiri) distribusi sample mean
Kita juga bisa menghitung standard deviation sebagai akar dari variansi
Sekarang kita hitung probabilitas yang diminta untuk distribusi sample mean, tetapi melalui distribusi normal tersebut (yaitu distribusi normal yang didekati oleh distribusi sample mean tersebut)
prob3 <-
pnorm(4.45, mean = xbar3_mean, sd = xbar3_var) -
pnorm(3.85, mean = xbar3_mean, sd = xbar3_var)
prob3[1] 0.832702Atau bisa kita ubah ke normal standar terlebih dahulu
standard_error <- x3_sd / sqrt(n3)
xbar3_lower <- 3.85
xbar3_upper <- 4.45
z3_lower <- (xbar3_lower - x3_mean) / standard_error
z3_upper <- (xbar3_upper - x3_mean) / standard_error
prob3_z <- pnorm(z3_upper) - pnorm(z3_lower)
prob3_z[1] 0.5227107Bagaimanapun juga, walaupun kita malah menghitung probabilitas menggunakan distribusi normal yang ditentukan di Dalil 1, kira-kira segitulah probabilitasnya di distribusi sample mean yang sebenarnya kita inginkan. Itulah manfaat dari Dalil 1, daripada harus bersusah payah membentuk distribusi sample mean terlebih dahulu.
Lalu bagaimana kalau tanpa pengembalian? Misalkan kita punya suatu populasi
[1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
[26] 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50Lihat sebarannya
Sample size 30, 1000 kali percobaan
Dapat terlihat juga bahwa bentuk distribusinya mirip dengan distribusi normal! Akan tetapi, rumus rata-rata dan variansi untuk distribusi normal tersebut agak berbeda (karena kali ini tanpa pengembalian), lihat Dalil 2 berikut!
Dalil 2
Apabila sampel acak berukuran \(n\) diambil secara acak tanpa pengembalian dari suatu populasi berhingga berukuran \(N\), dimana populasi tersebut memiliki mean \(\mu\) dan variansi \(\sigma^2\), maka distribusi probabilitas \(\bar{X}\) (sample mean) akan menghampiri distribusi normal \(N\left(\mu_{\bar{X}}, \sigma_{\bar{X}}^2\right)\), dengan
\[\mu_{\bar{X}} = \mu\]
\[\sigma_{\bar{X}}^2 = \frac{\sigma^2(N-n)}{n(N-1)}\]
Catatan: lagi-lagi, ada syarat \(n \geq 30\)
Secara umum, jika sampel yang diambil sangat besar (yaitu \(n \geq 30\)) maka bisa digunakan CLT atau Central Limit Theorem, juga disebut Dalil Limit Pusat
Semakin besar \(n\), yaitu ukuran dari sampel yang diambil (misalkan sampelnya memiliki rata-rata \(\mu\) dan variansi \(\sigma^2\)), distribusi sample mean nya makin mendekati distribusi normal \(N\left(\mu_{\bar{X}}, \sigma_{\bar{X}}^2\right)\), dengan
\[\mu_{\bar{X}} = \mu\]
\[\sigma_{\bar{X}}^2 = \frac{\sigma^2}{n}\]
Bagaimanapun bentuk distribusi aslinya, apabila \(n \geq 30\), distribusi normal di atas akan didekati oleh (ataupun mendekati) distribusi sample mean dengan sangat baik
Sebuah perusahaan memproduksi bohlam. Bila umur bohlam itu menyebar normal dengan mean 800 jam dan standar deviasi 40 jam, hitunglah peluang bahwa suatu sampel acak 16 bohlam akan mempunyai umur rata-rata kurang dari 775 jam.
Jawab: misalkan \(X\) adalah variabel acak untuk umur bohlam. Soal menanyakan terkait pengambilan sampel berukuran \(n=16\). Walaupun \(n < 30\), kebetulan \(X\) sudah berdistribusi normal (dengan \(\mu=800\) dan \(\sigma = 40\)), sehingga CLT masih bisa digunakan. Diminta
\[\text{Pr}(\bar{X} < 775)\]
yaitu CDF dari distribusi sample mean \(\bar{X}\) di nilai 775.
Mari kita data dulu informasi terkait \(X\) dan ukuran sampel
Sekarang kita hitung \(\mu_{\bar{X}}\) dan \(\sigma_{\bar{X}}^2\) berdasarkan CLT
Baru kita hitung \(\text{Pr}(\bar{X} < 775)\) dengan distribusi normal \(N\left(\mu_{\bar{X}}, \sigma_{\bar{X}}^2\right)\) tersebut
Atau jika ingin diubah ke dalam normal standar terlebih dahulu,
transformasi data random menjadi normal standar (berlaku untuk distribusi kontinu apapun -> sampling dist.) gunakan CLT -> scale
Distribusi-t digunakan saat \(n < 30\) (sehingga tidak bisa menggunakan CLT) dan variansi populasi tidak diketahui (yang ada hanyalah variasi sampel, misal \(S^2\)), sesuai Dalil 3 berikut
Apabila \(\bar{x}\) dan \(S^2\) masing-masing adalah nilai mean dan nilai variansi dari sampel berukuran \(n\), yang diambil dari suatu populasi normal dengan mean \(\mu\) (yang diketahui) dan variansi \(\sigma^2\) (yang tidak diketahui), maka kita bisa misalkan
\[t = \frac{\bar{x} - \mu}{\left( \frac{S}{\sqrt{n}} \right)}\]
dan \(t\) ini merupakan sebuah nilai dari variabel acak \(T\) yang mempunyai distribusi-t dengan (parameter) derajat bebas \(v = n-1\).
Distribusi-t adalah distribusi kontinu yang memiliki PDF dan CDF, sebagaimana distribusi kontinu pada umumnya, sehingga untuknya tersedia fungsi-fungsi d…, p…, q…, dan r… yang biasa kita kenal.
Distribusi-t memiliki satu parameter saja, yaitu degrees of freedom atau derajat bebas, yang dilambangkan df di R.
Pr(T<t)=0.05 (alpha) -> nyari t nya (t-table)
Tentukan nilai \(k\) sedemikian sehingga
\[\text{Pr}(k < T < -1.761) = 0.045\]
dari suatu sampel acak berukuran 15 diambil dari suatu populasi normal
Jawab:
Sebelumnya, perhatikan bahwa
\[\begin{align*} \text{Pr}&(k < T < -1.761) \\ &= \text{Pr}(T < -1.761) - \text{Pr}(T < k) \end{align*}\]
dan karena \(\text{Pr}(k < T < -1.761) = 0.045\), haruslah
\[\text{Pr}(T < -1.761) - \text{Pr}(T < k) = 0.045\]
sehingga
\[\text{Pr}(T < k) = \text{Pr}(T < -1.761) - 0.045\]
sehingga nantinya kita akan menghitung ruas kanan terlebih dahulu (manfaatkan CDF), kemudian memperoleh nilai \(k\) dengan quantile function yaitu inverse CDF.
Diketahui sampel acak berukuran \(n=15\). Maka, sesuai Dalil 3, parameter derajat bebas yang digunakan adalah
\[v = n-1 = 15-1 = 14\]
Perhatikan bahwa \(\text{Pr}(T < -1.761)\) adalah CDF di -1.761, yang bisa dihitung sebagai berikut
sehingga \(\text{Pr}(T < -1.761) - 0.045\) adalah
Maka,
\[\begin{align*} \text{Pr}&(T < k) \\ &= \text{Pr}(T < -1.761) - 0.045 \\ &\approx 0.005027095 \end{align*}\]
Kita bisa simpan dulu hasilnya,
Kemudian kita bisa menemukan nilai \(k\) yang memenuhi
\[\text{Pr}(T < k) \approx 0.005027095\]
dengan quantile function yaitu inverse CDF, sebagai berikut
Kesimpulannya,
\[k \approx -2.974114\]
Misalkan kita punya dua populasi (bisa sama ataupun berbeda), yang masing-masing dibuat distribusi sample mean nya, dan kita ingin melihat bagaimana selisih antara kedua distribusi sample mean tersebut. Secara tidak langsung, kita bisa melihat seberapa berbeda rata-rata antar kedua populasi, bagaimana persebaran bedanya.
Dalil 4 berikut adalah Dalil Limit Pusat yang telah disesuaikan untuk kasus dua populasi.
Misalkan
sampel acak berukuran \(n_1\) diambil secara acak dari populasi berukuran besar (tak hingga), misal Populasi I, dengan mean \(\mu_1\) dan variansi \(\sigma_1^2\).
sampel acak berukuran \(n_2\) diambil secara acak dari populasi berukuran besar (tak hingga), misal Populasi II, dengan mean \(\mu_2\) dan variansi \(\sigma_2^2\).
Populasi I dan Populasi II saling bebas.
Maka beda dua mean dari sampel, yaitu \(\bar{X}_1 - \bar{X}_2\), akan menyebar menghampiri distribusi normal \(N\left(\mu_{\bar{X}_1 - \bar{X}_2}, \sigma_{\bar{X}_1 - \bar{X}_2}^2\right)\) dengan mean dan variansi berikut:
\[\mu_{\bar{X}_1 - \bar{X}_2} = \mu_1 - \mu_2\]
\[\sigma_{\bar{X}_1 - \bar{X}_2}^2 = \frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}\]
Dengan demikian, misalkan
\[z= \frac{\left( \bar{x}_1 - \bar{x}_2 \right) - \left( \mu_1 - \mu_2 \right)}{\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}}\]
maka \(z\) merupakan nilai dari variabel acak normal standar \(Z\).
Catatan:
Distribusi tiap populasi tidak harus normal.
Apabila \(n_1 \geq 30\) dan \(n_2 \geq 30\), maka distribusi \(\bar{X}_1 - \bar{X}_2\) mendekati distribusi normal dengan sangat baik
Contoh:
Sebuah sampel acak berukuran \(n_1 = 5\) diambil secara acak dari sebuah populasi yang menyebar normal dengan nilai mean \(\mu_1 = 50\) dan \(\sigma_1^2 = 9\) dan diperoleh nilai mean sample nya \(\bar{x}_1\).
Sebuah sampel acak kedua berukuran \(n_2 = 4\), bebas dengan sampel acak pertama, diambil dari populasi lain yang jaga menyebar normal dengan nilai mean \(\mu_2 = 40\) dan \(\sigma_1^2 = 4\) dan diperoleh nilai mean sample nya \(\bar{x}_2\).
Tentukan nilai dari
\[\text{Pr}\left( \left(\bar{X}_1 - \bar{X}_2\right) < 8.2 \right)\]
Jawab:
Perhatikan bahwa nilai yang diminta adalah CDF di 8.2 dari variabel acak \(\bar{X}_1 - \bar{X}_2\).
Karena Populasi I dan Populasi II berdistribusi normal, walaupun \(n_1\) dan \(n_2\) berukuran kecil, maka \(\bar{X}_1 - \bar{X}_2\) juga berdistribusi normal.
(Kombinasi linear dari distribusi normal juga berupa distribusi normal.)
Mari kita data terlebih dahulu, semua yang diketahui dari soal
Kemudian, kita bisa mulai menerapkan Dalil 4.
Mean dari \(\bar{X}_1 - \bar{X}_2\) adalah:
\[\begin{align*} \mu_{\bar{X}_1 - \bar{X}_2} &= \mu_1 - \mu_2 \\ &= 50 - 40 = 10 \end{align*}\]
dan variansinya adalah:
\[\begin{align*} \sigma_{\bar{X}_1 - \bar{X}_2}^2 &= \frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2} \\ &= \frac{9}{5} + \frac{4}{4} \\ &= 2.8 \end{align*}\]
Kita juga bisa menghitung standard deviation untuk \(\bar{X}_1 - \bar{X}_2\) sebagai akar dari variansinya, seperti berikut
Jadi, mengikuti Dalil 4, kita bisa menghitung CDF dari \(\bar{X}_1 - \bar{X}_2\) melalui CDF dari distribusi normal yang dihampiri olehnya (ataupun menghampirinya), yaitu distribusi normal yang nilai rata-ratanya, variansinya, dan standard deviation-nya baru saja kita tentukan.
Dengan demikian, nilai \(\text{Pr}\left( \left(\bar{X}_1 - \bar{X}_2\right) < 8.2 \right)\) bisa dihitung melalui distribusi normal tersebut, sebagai berikut
Atau bisa juga kita ubah ke normal standar terlebih dahulu,
\[\begin{align*} \text{Pr}&\left( \left(\bar{X}_1 - \bar{X}_2\right) < 8.2 \right) \\ &= \text{Pr}\left( \frac{\left(\bar{X}_1 - \bar{X}_2\right) - 10}{\sqrt{2.8}} < \frac{8.2 - 10}{\sqrt{2.8}} \right) \\ &= \text{Pr}\left( Z < \frac{8.2 - 10}{\sqrt{2.8}} \right) \end{align*}\]
atau sama saja
Maka \[\begin{align*} \text{Pr}&\left( \left(\bar{X}_1 - \bar{X}_2\right) < 8.2 \right) \\ &= \text{Pr}\left( Z < \frac{8.2 - 10}{\sqrt{2.8}} \right) \\ &\approx 0.1410294 \end{align*}\]
Kesimpulannya, \[\begin{align*} \text{Pr}&\left( \left(\bar{X}_1 - \bar{X}_2\right) < 8.2 \right) \\ &\approx 0.1410294 \end{align*}\]