Modul 3 Persamaan Diferensial Numerik: Metode Runge-Kutta dan variasinya

Kembali ke Persamaan Diferensial Numerik

Format long

sin(pi/4)

ans = 0.7071

format long

sin(pi/4)

ans = 0.707106781186547

Kembali ke default:

format

sin(pi/4)

ans = 0.7071

Metode Runge-Kutta dan variasinya

Orde 2: Metode Midpoint

\[w_1=\alpha\] \[w_{i+1}=w_i+h f\left(t_i+\frac{h}{2}, w_i+\frac{h}{2} f\left(t_i, w_i\right)\right)\]

bisa juga ditulis,

\[w_1=\alpha\] \[m_1 = f\left(t_i, w_i\right)\] \[w_{i+1}=w_i+h f\left(t_i+\frac{h}{2}, w_i+\frac{h}{2} m_1\right)\]

atau bahkan,

\[w_1=\alpha\] \[m_1 = f\left(t_i, w_i\right)\] \[m_2 = f\left(t_i+\frac{h}{2}, w_i+\frac{h}{2} m_1\right)\] \[w_{i+1}=w_i+h m_2\]

Function file midpoint.m - nama file harus sama dengan nama fungsi

function [t, w] = midpoint(f, a, b, N, alpha)
  h = (b - a) / N;
  t = zeros(N + 1, 1);
  w = zeros(N + 1, 1);
  t(1) = a;
  w(1) = alpha;
  for i = 1 : N
    t(i + 1) = t(i) + h;
    m1 = f(t(i), w(i));
    m2 = f(t(i) + (h / 2), w(i) + (h / 2) * m1);
    w(i + 1) = w(i) + h * m2;
  endfor
endfunction

Misalkan diberikan MNA sebagai berikut, yang ingin diselesaikan secara numerik dengan \(N = 10\):

\[y' = y - t^2 + 1\] \[0 \le t \le 2\] \[y(0) = 0.5\]

yang kebetulan memiliki solusi eksak:

\[y\left(t\right) = \left( t + 1 \right)^2 - 0.5 e^t\]

Contoh penggunaan:

Script file coba_midpoint.m - nama file bebas

f = @(t, y) (y - t .^ 2 + 1);
a = 0;
b = 2;
N = 10;
alpha = 0.5;

[t, w] = midpoint(f, a, b, N, alpha);

sln = @(t) (t + 1) .^ 2 - 0.5 * exp(t);
y_eksak = sln(t);

err_midpoint = abs(w - y_eksak);
err_midpoint_total = sum(err_midpoint); % norm L1 (taxicab/Manhattan)

disp("Tabel aproksimasi w, solusi eksak y, dan error:");
[t, w, y_eksak, err_midpoint]
disp("Error total (norm L1):");
disp(err_midpoint_total);

hold on;
fplot(sln, [a, b], 'b');
scatter(t, w, 'r');
legend("Solusi Eksak", "Metode Midpoint");

Tabel aproksimasi w, solusi eksak y, dan error:
ans =

        0   0.5000   0.5000        0
   0.2000   0.8280   0.8293   0.0013
   0.4000   1.2114   1.2141   0.0027
   0.6000   1.6447   1.6489   0.0043
   0.8000   2.1213   2.1272   0.0059
   1.0000   2.6332   2.6409   0.0077
   1.2000   3.1705   3.1799   0.0095
   1.4000   3.7212   3.7324   0.0112
   1.6000   4.2706   4.2835   0.0129
   1.8000   4.8010   4.8152   0.0142
   2.0000   5.2904   5.3055   0.0151

Error total (norm L1):
0.084840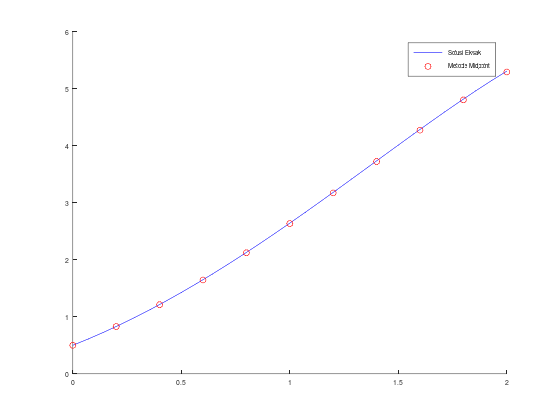

Orde 2: Metode Modified Euler

\[w_1=\alpha\] \[w_{i+1}=w_i+\frac{h}{2}\left(f\left(t_i, w_i\right)+f\left(t_{i+1}, w_i+h f\left(t_i, w_i\right)\right)\right)\]

bisa juga ditulis,

\[w_1=\alpha\] \[m_1 = f\left(t_i, w_i\right)\] \[w_{i+1}=w_i+\frac{h}{2}\left(m_1+f\left(t_{i+1}, w_i+h m_1\right)\right)\]

atau bahkan,

\[w_1=\alpha\] \[m_1 = f\left(t_i, w_i\right)\] \[m_2 = f\left(t_{i+1}, w_i+h m_1\right)\] \[w_{i+1}=w_i+\frac{h}{2}\left(m_1+m_2\right)\]

Function file modified_euler.m - nama file harus sama dengan nama fungsi

function [t, w] = modified_euler(f, a, b, N, alpha)
  h = (b - a) / N;
  t = zeros(N + 1, 1);
  w = zeros(N + 1, 1);
  t(1) = a;
  w(1) = alpha;
  for i = 1 : N
    t(i + 1) = t(i) + h;
    m1 = f(t(i), w(i));
    m2 = f(t(i + 1), w(i) + h * m1);
    w(i + 1) = w(i) + h * (m1 + m2) / 2;
  endfor
endfunction

Misalkan diberikan MNA sebagai berikut, yang ingin diselesaikan secara numerik dengan \(N = 10\):

\[y' = y - t^2 + 1\] \[0 \le t \le 2\] \[y(0) = 0.5\]

dan misalkan solusi eksak tidak diketahui.

Contoh penggunaan (perbandingan metode Runge-Kutta orde 2):

Script file bandingkan_rko2.m - nama file bebas

f = @(t, y) (y - t .^ 2 + 1);
a = 0;
b = 2;
N = 10;
alpha = 0.5;

[t1, w1] = midpoint(f, a, b, N, alpha);
[t2, w2] = modified_euler(f, a, b, N, alpha);

[t1, w1, w2]

hold on;
scatter(t1, w1, 'r');
scatter(t2, w2, 'g');
legend("Midpoint", "Modified Euler");

ans =

        0   0.5000   0.5000
   0.2000   0.8280   0.8260
   0.4000   1.2114   1.2069
   0.6000   1.6447   1.6372
   0.8000   2.1213   2.1102
   1.0000   2.6332   2.6177
   1.2000   3.1705   3.1496
   1.4000   3.7212   3.6937
   1.6000   4.2706   4.2351
   1.8000   4.8010   4.7556
   2.0000   5.2904   5.2331

Misalkan diketahui solusi eksak:

\[y\left(t\right) = \left( t + 1 \right)^2 - 0.5 e^t\]

Maka kita juga bisa menghitung error dari masing-masing metode.

Script file bandingkan2_rko2.m - nama file bebas

f = @(t, y) (y - t .^ 2 + 1);
a = 0;
b = 2;
N = 10;
alpha = 0.5;

[t1, w1] = midpoint(f, a, b, N, alpha);
[t2, w2] = modified_euler(f, a, b, N, alpha);

sln = @(t) (t + 1) .^ 2 - 0.5 * exp(t);
y_eksak = sln(t1);

err1 = abs(y_eksak - w1);
err2 = abs(y_eksak - w2);

[t1, y_eksak, w1, err1, w2, err2]

hold on;
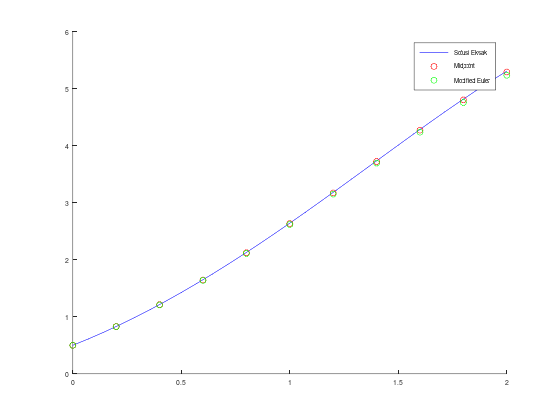
fplot(sln, [a, b], 'b');
scatter(t1, w1, 'r');
scatter(t2, w2, 'g');
legend("Solusi Eksak", "Midpoint", "Modified Euler");

ans =

        0   0.5000   0.5000        0   0.5000        0
   0.2000   0.8293   0.8280   0.0013   0.8260   0.0033
   0.4000   1.2141   1.2114   0.0027   1.2069   0.0072
   0.6000   1.6489   1.6447   0.0043   1.6372   0.0117
   0.8000   2.1272   2.1213   0.0059   2.1102   0.0170
   1.0000   2.6409   2.6332   0.0077   2.6177   0.0232
   1.2000   3.1799   3.1705   0.0095   3.1496   0.0304
   1.4000   3.7324   3.7212   0.0112   3.6937   0.0387
   1.6000   4.2835   4.2706   0.0129   4.2351   0.0484
   1.8000   4.8152   4.8010   0.0142   4.7556   0.0596
   2.0000   5.3055   5.2904   0.0151   5.2331   0.0724

Orde 3: Metode Heun

\[w_1=\alpha\] \[w_{i+1}=w_i+\frac{h}{4}\left(f\left(t_i, w_i\right)+3 f\left(t_i+\frac{2 h}{3}, w_i+\frac{2 h}{3} f\left(t_i+\frac{h}{3}, w_i+\frac{h}{3} f\left(t_i, w_i\right)\right)\right)\right)\]

bisa juga ditulis,

\[w_1=\alpha\] \[m_1 = f\left(t_i, w_i\right)\] \[w_{i+1}=w_i+\frac{h}{4}\left(m_1+3 f\left(t_i+\frac{2 h}{3}, w_i+\frac{2 h}{3} f\left(t_i+\frac{h}{3}, w_i+\frac{h}{3} m_1\right)\right)\right)\]

atau,

\[w_1=\alpha\] \[m_1 = f\left(t_i, w_i\right)\] \[m_2 = f\left(t_i+\frac{h}{3}, w_i+\frac{h}{3} m_1\right)\] \[w_{i+1}=w_i+\frac{h}{4}\left(m_1+3 f\left(t_i+\frac{2 h}{3}, w_i+\frac{2 h}{3} m_2\right)\right)\]

atau bahkan,

\[w_1=\alpha\] \[m_1 = f\left(t_i, w_i\right)\] \[m_2 = f\left(t_i+\frac{h}{3}, w_i+\frac{h}{3} m_1\right)\] \[m_3 = f\left(t_i+\frac{2 h}{3}, w_i+\frac{2 h}{3} m_2\right)\] \[w_{i+1}=w_i+\frac{h}{4}\left(m_1+3 m_3\right)\]

Function file heun.m - nama file harus sama dengan nama fungsi

function [t, w] = heun(f, a, b, N, alpha)
  h = (b - a) / N;
  t = zeros(N + 1, 1);
  w = zeros(N + 1, 1);
  t(1) = a;
  w(1) = alpha;
  for i = 1 : N
    t(i + 1) = t(i) + h;
    m1 = f(t(i), w(i));
    m2 = f(t(i) + (h / 3), w(i) + (h / 3) * m1);
    m3 = f(t(i) + (2 * h / 3), w(i) + (2 * h / 3) * m2);
    w(i + 1) = w(i) + (h / 4) * (m1 + 3 * m3);
  endfor
endfunction

Misalkan diberikan MNA sebagai berikut, yang ingin diselesaikan secara numerik dengan \(N = 10\):

\[y' = y - t^2 + 1\] \[0 \le t \le 2\] \[y(0) = 0.5\]

yang kebetulan memiliki solusi eksak:

\[y\left(t\right) = \left( t + 1 \right)^2 - 0.5 e^t\]

Contoh penggunaan:

Script file coba_heun.m - nama file bebas

f = @(t, y) (y - t .^ 2 + 1);
a = 0;
b = 2;
N = 10;
alpha = 0.5;

[t, w] = heun(f, a, b, N, alpha);

sln = @(t) (t + 1) .^ 2 - 0.5 * exp(t);
y_eksak = sln(t);

err_heun = abs(w - y_eksak);
err_heun_total = sum(err_heun); % norm L1 (taxicab/Manhattan)

disp("Tabel aproksimasi w, solusi y, dan error:");
[t, w, y_eksak, err_heun]
disp("Error total (norm L1):");
disp(err_heun_total);

hold on;
fplot(sln, [a, b], 'b');
scatter(t, w, 'r');
legend("Solusi Eksak", "Metode Heun");

Tabel aproksimasi w, solusi y, dan error:
ans =

        0   0.5000   0.5000        0
   0.2000   0.8292   0.8293   0.0001
   0.4000   1.2140   1.2141   0.0001
   0.6000   1.6488   1.6489   0.0002
   0.8000   2.1270   2.1272   0.0002
   1.0000   2.6406   2.6409   0.0003
   1.2000   3.1796   3.1799   0.0004
   1.4000   3.7320   3.7324   0.0004
   1.6000   4.2830   4.2835   0.0005
   1.8000   4.8147   4.8152   0.0005
   2.0000   5.3050   5.3055   0.0005

Error total (norm L1):
3.0743e-03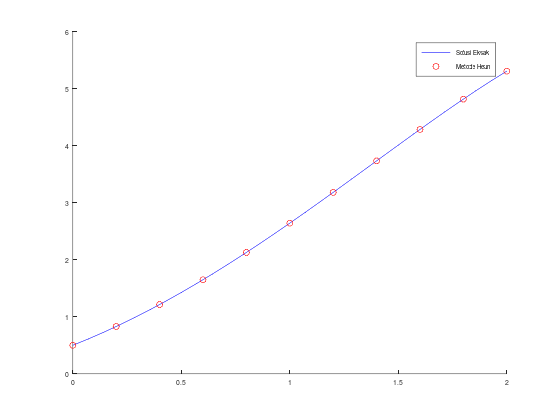

Ternyata errornya sangat kecil! KIta bisa melihat errornya dengan lebih detail/presisi, dengan menggunakan format long

Script file coba2_heun.m - nama file bebas

f = @(t, y) (y - t .^ 2 + 1);
a = 0;
b = 2;
N = 10;
alpha = 0.5;

[t, w] = heun(f, a, b, N, alpha);

sln = @(t) (t + 1) .^ 2 - 0.5 * exp(t);
y_eksak = sln(t);

err_heun = abs(w - y_eksak);
err_heun_total = sum(err_heun); % norm L1 (taxicab/Manhattan)

format long; % pasang format output menjadi panjang (lebih presisi)
disp("Tabel aproksimasi w, solusi y, dan error:");
[t, w, y_eksak, err_heun]
disp("Error total (norm L1):");
disp(err_heun_total);
format; % kembali ke ukuran default

hold on;
fplot(sln, [a, b], 'b');
scatter(t, w, 'r');
legend("Solusi Eksak", "Metode Heun");

Tabel aproksimasi w, solusi y, dan error:
ans =

                   0   0.500000000000000   0.500000000000000                   0
   0.200000000000000   0.829244444444444   0.829298620919915   0.000054176475471
   0.400000000000000   1.213974992592593   1.214087651179365   0.000112658586772
   0.600000000000000   1.648765902064198   1.648940599804746   0.000174697740548
   0.800000000000000   2.126990532832184   2.127229535753766   0.000239002921582
   1.000000000000000   2.640555548543485   2.640859085770478   0.000303537226992
   1.200000000000000   3.179576287732221   3.179941538631727   0.000365250899506
   1.400000000000000   3.731980283861397   3.732400016577663   0.000419732716265
   1.600000000000000   4.283023031133831   4.283483787802441   0.000460756668610
   1.800000000000000   4.814696573135897   4.815176267793527   0.000479694657630
   2.000000000000000   5.305007192434419   5.305471950534676   0.000464758100256

Error total (norm L1):
3.074265993633474e-03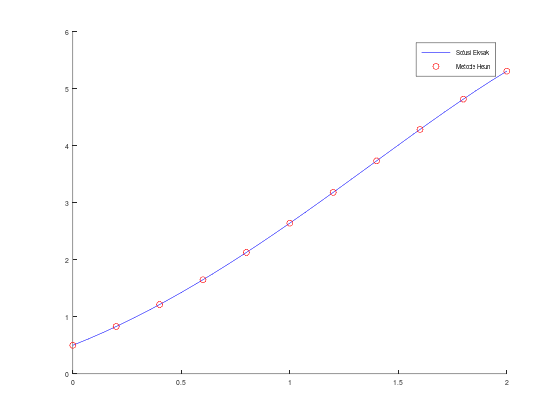

Metode Runge-Kutta orde 4

\[w_1=\alpha\] \[k_1=h f\left(t_i, w_i\right)\] \[k_2=h f\left(t_i+\frac{h}{2}, w_i+\frac{k_1}{2}\right)\] \[k_3=h f\left(t_i+\frac{h}{2}, w_i+\frac{k_2}{2}\right)\] \[k_4=h f\left(t_{i+1}, w_i+k_3\right)\] \[w_{i+1}=w_i+\frac{1}{6}\left(k_1+2 k_2+2 k_3+k_4\right)\]

Function file rko4.m - nama file harus sama dengan nama fungsi

function [t, w] = rko4(f, a, b, N, alpha)
  h = (b - a) / N;
  t = zeros(N + 1, 1);
  w = zeros(N + 1, 1);
  t(1) = a;
  w(1) = alpha;
  for i = 1 : N
    t(i + 1) = t(i) + h;
    k1 = h * f(t(i), w(i));
    k2 = h * f(t(i) + (h / 2), w(i) + (k1 / 2));
    k3 = h * f(t(i) + (h / 2), w(i) + (k2 / 2));
    k4 = h * f(t(i + 1), w(i) + k3);
    w(i + 1) = w(i) + (k1 + 2 * k2 + 2 * k3 + k4) / 6;
  endfor
endfunction

Misalkan diberikan MNA sebagai berikut, yang ingin diselesaikan secara numerik dengan \(N = 10\):

\[y' = y - t^2 + 1\] \[0 \le t \le 2\] \[y(0) = 0.5\]

yang kebetulan memiliki solusi eksak:

\[y\left(t\right) = \left( t + 1 \right)^2 - 0.5 e^t\]

Script file coba_rko4.m - nama file bebas

f = @(t, y) (y - t .^ 2 + 1);
a = 0;
b = 2;
N = 10;
alpha = 0.5;

[t, w] = rko4(f, a, b, N, alpha);

sln = @(t) (t + 1) .^ 2 - 0.5 * exp(t);
y_eksak = sln(t);

err_rko4 = abs(w - y_eksak);
err_rko4_total = sum(err_rko4); % norm L1 (taxicab/Manhattan)

format long; % pasang format output menjadi panjang (lebih presisi)
disp("Tabel aproksimasi w, solusi y, dan error:");
[t, w, y_eksak, err_rko4]
disp("Error total (norm L1):");
disp(err_rko4_total);
format; % kembali ke ukuran default

hold on;
fplot(sln, [a, b], 'b');
scatter(t, w, 'r');
legend("Solusi Eksak", "Metode Runge-Kutta orde 4");

Tabel aproksimasi w, solusi y, dan error:
ans =

                   0   0.500000000000000   0.500000000000000                   0
   0.200000000000000   0.829293333333333   0.829298620919915   0.000005287586582
   0.400000000000000   1.214076210666667   1.214087651179365   0.000011440512698
   0.600000000000000   1.648922017041600   1.648940599804746   0.000018582763146
   0.800000000000000   2.127202684947944   2.127229535753766   0.000026850805823
   1.000000000000000   2.640822692728752   2.640859085770478   0.000036393041726
   1.200000000000000   3.179894170232231   3.179941538631727   0.000047368399497
   1.400000000000000   3.732340072854980   3.732400016577663   0.000059943722683
   1.600000000000000   4.283409498318406   4.283483787802441   0.000074289484035
   1.800000000000000   4.815085694579435   4.815176267793527   0.000090573214092
   2.000000000000000   5.305363000692655   5.305471950534676   0.000108949842021

Error total (norm L1):
4.796793723015336e-04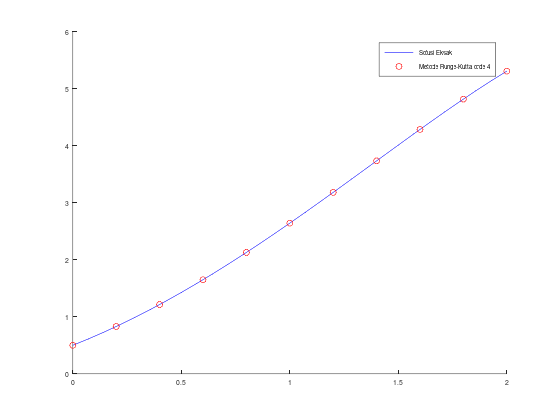

Perbandingan metode Runge-Kutta orde 2, 3, 4

Misalkan diberikan MNA sebagai berikut, yang ingin diselesaikan secara numerik dengan \(N = 10\):

\[y' = y - t^2 + 1\] \[0 \le t \le 2\] \[y(0) = 0.5\]

yang kebetulan memiliki solusi eksak:

\[y\left(t\right) = \left( t + 1 \right)^2 - 0.5 e^t\]

Script file bandingkan_rk234.m - nama file bebas

f = @(t, y) (y - t .^ 2 + 1);
a = 0;
b = 2;
N = 10;
alpha = 0.5;

[t1, w1] = midpoint(f, a, b, N, alpha);
[t2, w2] = modified_euler(f, a, b, N, alpha);
[t3, w3] = heun(f, a, b, N, alpha);
[t4, w4] = rko4(f, a, b, N, alpha);

sln = @(t) (t + 1) .^ 2 - 0.5 * exp(t);
y_eksak = sln(t1);

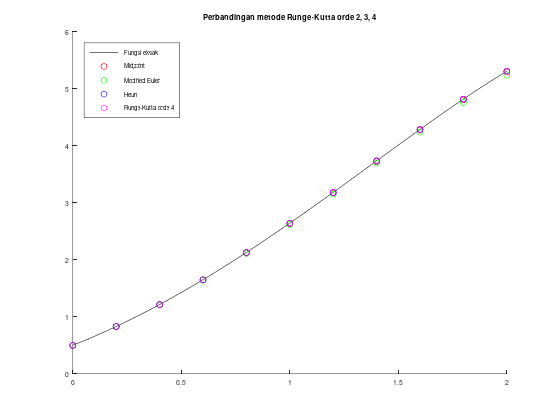
[t1, w1, w2, w3, w4, y_eksak]

hold on;
fplot(sln, [a, b], 'k');
scatter(t1, w1, 'r');
scatter(t2, w2, 'g');
scatter(t3, w3, 'b');
scatter(t4, w4, 'm');
legend('Fungsi eksak', 'Midpoint', 'Modified Euler', 'Heun', 'Runge-Kutta orde 4');
legend("location", "northwest");
title('Perbandingan metode Runge-Kutta orde 2, 3, 4');

ans =

        0   0.5000   0.5000   0.5000   0.5000   0.5000
   0.2000   0.8280   0.8260   0.8292   0.8293   0.8293
   0.4000   1.2114   1.2069   1.2140   1.2141   1.2141
   0.6000   1.6447   1.6372   1.6488   1.6489   1.6489
   0.8000   2.1213   2.1102   2.1270   2.1272   2.1272
   1.0000   2.6332   2.6177   2.6406   2.6408   2.6409
   1.2000   3.1705   3.1496   3.1796   3.1799   3.1799
   1.4000   3.7212   3.6937   3.7320   3.7323   3.7324
   1.6000   4.2706   4.2351   4.2830   4.2834   4.2835
   1.8000   4.8010   4.7556   4.8147   4.8151   4.8152
   2.0000   5.2904   5.2331   5.3050   5.3054   5.3055