function [t, w1, w2] = rko4_sys2(f1, f2, a, b, N, alph1, alph2)
h = (b - a)/N;
t = w1 = w2 = [];
t(1) = a;
w1(1) = alph1;
w2(1) = alph2;
for i = 1:N
k11 = h * f1(t(i), w1(i), w2(i));
k12 = h * f2(t(i), w1(i), w2(i));
k21 = h * f1((t(i)+(h/2)), (w1(i)+(k11/2)), (w2(i)+(k12/2)));
k22 = h * f2((t(i)+(h/2)), (w1(i)+(k11/2)), (w2(i)+(k12/2)));
k31 = h * f1((t(i)+(h/2)), (w1(i)+(k21/2)), (w2(i)+(k22/2)));
k32 = h * f2((t(i)+(h/2)), (w1(i)+(k21/2)), (w2(i)+(k22/2)));
k41 = h * f1((t(i)+h), (w1(i)+k31), (w2(i)+k32));
k42 = h * f2((t(i)+h), (w1(i)+k31), (w2(i)+k32));
w1(i+1) = w1(i) + (k11 + 2*k21 + 2*k31 + k41)/6;
w2(i+1) = w2(i) + (k12 + 2*k22 + 2*k32 + k42)/6;
t(i+1) = a + i*h;
endfor
endfunctionModul 5 Persamaan Diferensial Numerik: Sistem PDB orde 1 dan PDB orde tinggi
Kembali ke Persamaan Diferensial Numerik
Sistem Persamaan Diferensial: (fourth-order) Runge-Kutta for Systems
Bentuk umum
Bentuk umum sistem Persamaan Diferensial:
\(u'_1 = f_1(t,u_1,u_2,...,u_m)\)
\(u'_2 = f_2(t,u_1,u_2,...,u_m)\)
\(...\)
\(u'_m = f_m(t,u_1,u_2,...,u_m)\)
dengan:
\(a \leq t \leq b\)
\(u_1(a)=a_1, u_2(a)=a_2, ..., u_m(a)=a_m\) (initial value)
Bentuk umum algoritma metode untuk sistem PDB orde 1
for i = 1 : N do
for R in (rumus-rumus untuk iterasi ke-i) do
for j = 1 : m do
Hitung R dengan f_j
endfor
endfor
endforMisalnya, apabila ada lima rumus (seperti dalam metode Runge-Kutta orde 4), algoritma untuk sistem menjadi:
for i = 1 : N do
for j = 1 : m do
Hitung Rumus1 dengan f_j
endfor
for j = 1 : m do
Hitung Rumus2 dengan f_j
endfor
for j = 1 : m do
Hitung Rumus3 dengan f_j
endfor
for j = 1 : m do
Hitung Rumus4 dengan f_j
endfor
for j = 1 : m do
Hitung Rumus5 dengan f_j
endfor
endforApabila misalnya rumus pada iterasi 1, 2, 3 berbeda dengan rumus pada iterasi 4+ (seperti untuk metode Adams predictor-corrector orde 4), algoritma untuk sistem bisa seperti berikut:
for i = 1 : 3 do
for j = 1 : m do
Hitung Rumus1 dengan f_j
endfor
for j = 1 : m do
Hitung Rumus2 dengan f_j
endfor
for j = 1 : m do
Hitung Rumus3 dengan f_j
endfor
for j = 1 : m do
Hitung Rumus4 dengan f_j
endfor
for j = 1 : m do
Hitung Rumus5 dengan f_j
endfor
endfor
for i = 4 : N do
for j = 1 : m do
Hitung Rumus1 dengan f_j
endfor
for j = 1 : m do
Hitung Rumus2 dengan f_j
endfor
endforFunction file: (fourth-order) Runge-Kutta for systems
Pada modul ini, akan dibahas mengenai metode Runge-Kutta orde 4 untuk menyelesaikan sistem persamaan diferensial. Berikut merupakan code dari metode Runge-Kutta untuk sistem persamaan diferensial pada Octave yang perlu disimpan pada function file.
Untuk dua PDB:
Untuk m PDB:
function [t, w] = rko4_sysm(cell_f, a, b, N, alphas)
m = length(cell_f);
h = (b - a) / N;
t = zeros(N + 1, 1);
w = zeros(m, N + 1);
t(1) = a;
w(:, 1) = alphas;
k1 = zeros(m, 1);
k2 = zeros(m, 1);
k3 = zeros(m, 1);
k4 = zeros(m, 1);
for i = 1 : N
t(i + 1) = t(i) + h;
for j = 1 : m
k1(j) = h * cell_f{j}(t(i), w(:, i));
endfor
for j = 1 : m
k2(j) = h * cell_f{j}(t(i) + (h / 2), w(:, i) + (k1 / 2));
endfor
for j = 1 : m
k3(j) = h * cell_f{j}(t(i) + (h / 2), w(:, i) + (k2 / 2));
endfor
for j = 1 : m
k4(j) = h * cell_f{j}(t(i + 1), w(:, i) + k3);
endfor
for j = 1 : m
w(j, i + 1) = w(j, i) + (k1(j) + 2 * k2(j) + 2 * k3(j) + k4(j)) / 6;
endfor
endfor
endfunctionContoh sistem PD
\(u'_1 = -4u_1+3u_2+6, \;u_1(0)=0\)
\(u'_2 = -2.4u_1+1.6u_2+3.6, \;u_2(0)=0\)
Akan diuji dengan \(h=0.1\) dan \(0\leq t \leq 0.5\)
Solusi eksak:
\(u_1(t)=-3.375e^{-2t}+1.875e^{-0.4t}+1.5\)
\(u_2(t) = -2.25e^{-2t}+2.25e^{-0.4t}\)
Berikut adalah code script file untuk menjalankan function metode Runge-Kutta untuk sistem PD di atas (menggunakan yang khusus dua persamaan):
f1 = @(t, y1, y2) (-4*y1 + 3*y2 + 6);
f2 = @(t, y1, y2) (-2.4*y1 + 1.6*y2 + 3.6);
a = 0;
b = 0.5;
N = 5;
alph1 = 0;
alph2 = 0;
[t, w1, w2] = rko4_sys2(f1, f2, a, b, N, alph1, alph2);
sln1 = @(t) (-3.375*exp(-2*t) + 1.875*exp(-0.4*t) + 1.5);
sln2 = @(t) (-2.25*exp(-2*t) + 2.25*exp(-0.4*t));
w1ex = w2ex = [];
for i = 1:length(t)
w1ex(i) = sln1(t(i));
w2ex(i) = sln2(t(i));
endfor
[t', w1', w2', w1ex', w2ex']
hold on;
fplot(sln1, [a, b], 'r');
fplot(sln2, [a, b], 'b');
scatter(t, w1, 'r');
scatter(t, w2, 'b');
legend('u1', 'u2');
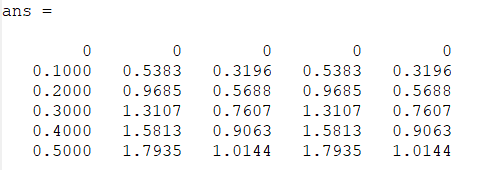
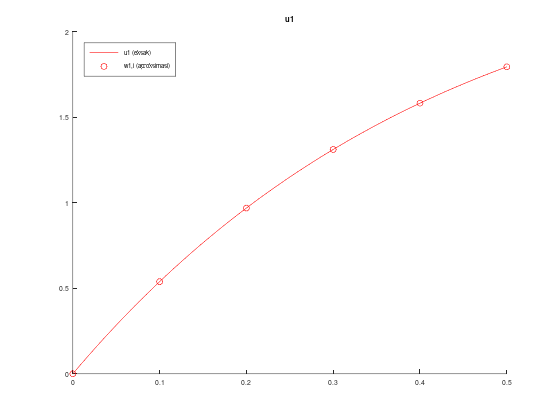
legend('location', 'northwest');Jika kita run script file tersebut, maka program akan mengeluarkan dua macam output, yaitu tabel serta plot perbandingan solusi eksak dan aproksimasi seperti di bawah ini:
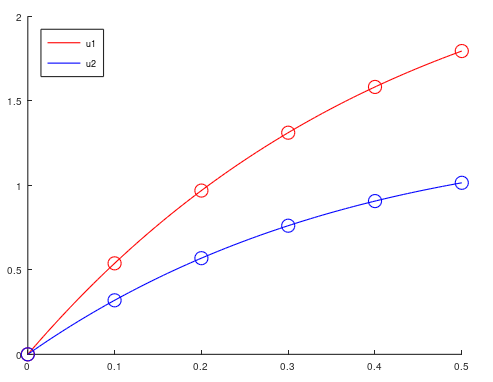
Berikut conoth script file menggunakan kode yang untuk m persamaan.
f1 = @(t, u) (-4*u(1) + 3*u(2) + 6);
f2 = @(t, u) (-2.4*u(1) + 1.6*u(2) + 3.6);
a = 0;
b = 0.5;
N = 5;
alpha1 = 0;
alpha2 = 0;
[t, w] = rko4_sysm({f1, f2}, a, b, N, [alpha1, alpha2]);
sln1 = @(t) (-3.375*exp(-2*t) + 1.875*exp(-0.4*t) + 1.5);
sln2 = @(t) (-2.25*exp(-2*t) + 2.25*exp(-0.4*t));
u1_eksak = sln1(t);
u2_eksak = sln2(t);
[t, w', u1_eksak, u2_eksak]
hold on;
fplot(sln1, [a, b], 'r');
scatter(t, w(1, :), 'r'); % ambil baris pertama yaitu solusi u1
fplot(sln2, [a, b], 'b');
scatter(t, w(2, :), 'b'); % ambil baris kedua yaitu solusi u2
legend('u1 (eksak)', 'w1,i', 'u2 (eksak)', 'w2,i');
legend('location', 'northwest');ans =
0 0 0 0 0
0.1000 0.5383 0.3196 0.5383 0.3196
0.2000 0.9685 0.5688 0.9685 0.5688
0.3000 1.3107 0.7607 1.3107 0.7607
0.4000 1.5813 0.9063 1.5813 0.9063
0.5000 1.7935 1.0144 1.7935 1.0144
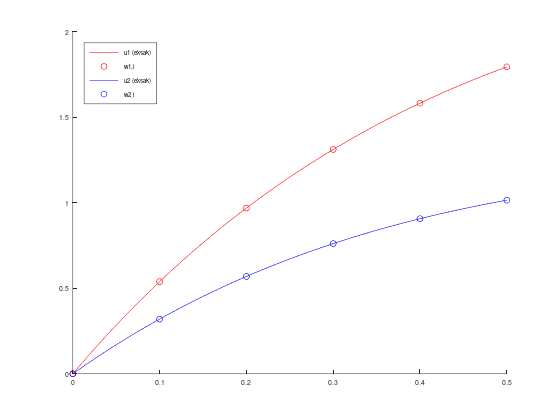
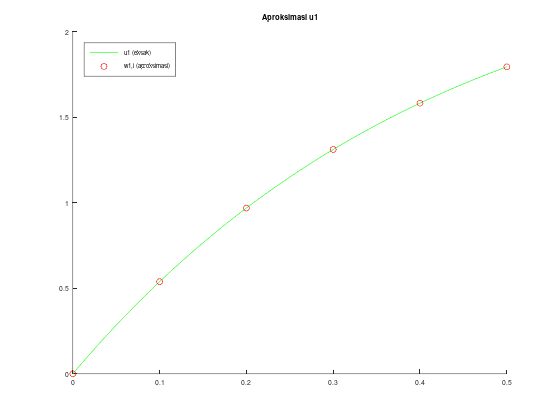
Sebenarnya, kita bisa saja menampilkan dua plot yang terpisah, menggunakan perintah figure. Selain itu, tabelnya juga bisa dipisah antara tabel untuk \(u_1\) dan tabel untuk \(u_2\), sekaligus menghitung dan menampilkan error.
f1 = @(t, u) (-4*u(1) + 3*u(2) + 6);
f2 = @(t, u) (-2.4*u(1) + 1.6*u(2) + 3.6);
a = 0;
b = 0.5;
N = 5;
alpha1 = 0;
alpha2 = 0;
[t, w] = rko4_sysm({f1, f2}, a, b, N, [alpha1, alpha2]);
sln1 = @(t) (-3.375*exp(-2*t) + 1.875*exp(-0.4*t) + 1.5);
sln2 = @(t) (-2.25*exp(-2*t) + 2.25*exp(-0.4*t));
u1_eksak = sln1(t);
u2_eksak = sln2(t);
% menghitung error
err_w1 = abs(w(1, :)' - u1_eksak);
err_w2 = abs(w(2, :)' - u2_eksak);
err_w1_total = sum(err_w1); % norm L1 (taxicab/Manhattan)
err_w2_total = sum(err_w2); % norm L1 (taxicab/Manhattan)
% menampilkan tabel, termasuk error
format long;
disp("Tabel aproksimasi w1,i, solusi eksak u1(t), dan error:");
[t, w(1, :)', u1_eksak, err_w1]
disp("Tabel aproksimasi w2,i, solusi eksak u2(t), dan error:");
[t, w(2, :)', u2_eksak, err_w2]
disp("Error total (norm L1) untuk w1,i:");
disp(err_w1_total);
disp("Error total (norm L1) untuk w2,i:");
disp(err_w2_total);
format;
figure;
hold on;
fplot(sln1, [a, b], 'g');
scatter(t, w(1, :), 'r'); % ambil baris pertama yaitu solusi u1
title("Aproksimasi u1");
legend("u1 (eksak)", "w1,i (aproksimasi)")
legend('location', 'northwest');
figure;
hold on;
fplot(sln2, [a, b], 'g');
scatter(t, w(2, :), 'b'); % ambil baris kedua yaitu solusi u2
title("Aproksimasi u2");
legend("u2 (eksak)", "w2,i (aproksimasi)")
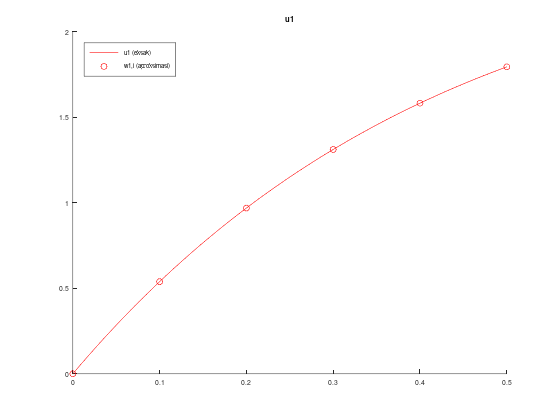
legend('location', 'northwest');Tabel aproksimasi w1,i, solusi eksak u1(t), dan error:
ans =
0 0 0 0
0.100000000000000 0.538255200000000 0.538263906772417 0.000008706772417
0.200000000000000 0.968498737529088 0.968512994104659 0.000014256575571
0.300000000000000 1.310719039205257 1.310736547027331 0.000017507822074
0.400000000000000 1.581265238963142 1.581284350416023 0.000019111452881
0.500000000000000 1.793507490120283 1.793527048067598 0.000019557947315
Tabel aproksimasi w2,i, solusi eksak u2(t), dan error:
ans =
0 0 0 0
0.100000000000000 0.319626240000000 0.319632043667268 0.000005803667268
0.200000000000000 0.568782173034906 0.568791675789742 0.000009502754836
0.300000000000000 0.760733131868175 0.760744801402045 0.000011669533870
0.400000000000000 0.906320617948927 0.906333355910227 0.000012737961300
0.500000000000000 1.014402416769883 1.014415451789714 0.000013035019830
Error total (norm L1) untuk w1,i:
7.914057025892873e-05
Error total (norm L1) untuk w2,i:
5.274893710444095e-05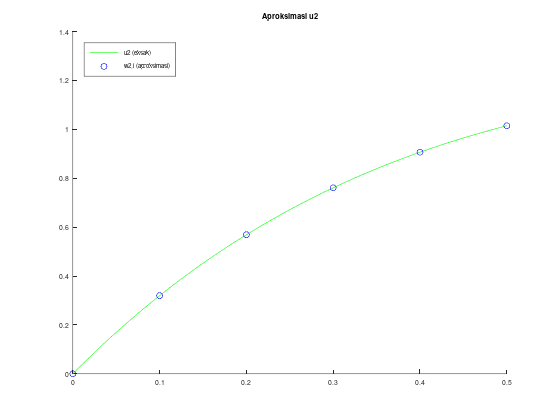
Contoh lain: untuk metode Taylor orde \(n\)
function [t, w] = taylor_sysm(cell_f, cell_fp, a, b, N, alphas)
m = length(cell_f);
h = (b - a) / N;
n = length(cell_fp{1}) + 1;
t = zeros(N + 1, 1);
w = zeros(m, N + 1);
t(1) = a;
w(:, 1) = alphas;
for i = 1 : N
t(i + 1) = t(i) + h;
for j = 1 : m
T = cell_f{j}(t(i), w(:, i));
for p = 2 : n
T += h^(p-1) * cell_fp{j}{p-1}(t(i), w(:, i)) / factorial(p);
endfor
w(j, i + 1) = w(j, i) + h * T;
endfor
endfor
endfunctionMencoba masalah yang sama,
\(u'_1 = -4u_1+3u_2+6, \;u_1(0)=0\)
\(u'_2 = -2.4u_1+1.6u_2+3.6, \;u_2(0)=0\)
Akan diuji dengan \(h=0.1\) dan \(0\leq t \leq 0.5\)
Solusi eksak:
\(u_1(t)=-3.375e^{-2t}+1.875e^{-0.4t}+1.5\)
\(u_2(t) = -2.25e^{-2t}+2.25e^{-0.4t}\)
Perhatikan bahwa
\[u_1' = f_1(t, u_1, u_2) = -4u_1+3u_2+6\]
\[u_2' = f_2(t, u_1, u_2) = -2.4u_1+1.6u_2+3.6\]
Contoh \(n=1\) (metode Euler)
Apabila kita tidak menyediakan turunan (terhadap \(t\)) dari \(f_1\) maupun dari \(f_2\), maka \(n=1\), yaitu metode Taylor orde \(n\) menjadi metode Euler.
f1 = @(t, u) (-4*u(1) +3*u(2) + 6);
turunan_f1 = {}; % tidak menyediakan turunan f1 terhadap t
f2 = @(t, u) (-2.4*u(1) + 1.6*u(2) + 3.6);
turunan_f2 = {}; % tidak menyediakan turunan f2 terhadap t
a = 0;
b = 0.5;
h = 0.1;
N = (b - a) / h;
alpha1 = 0;
alpha2 = 0;
[t, w] = taylor_sysm({f1, f2}, {turunan_f1, turunan_f2}, a, b, N, [alpha1, alpha2]);
sln1 = @(t) (-3.375*exp(-2*t) + 1.875*exp(-0.4*t) + 1.5);
sln2 = @(t) (-2.25*exp(-2*t) + 2.25*exp(-0.4*t));
u1_eksak = sln1(t);
u2_eksak = sln2(t);
% menghitung error
err_w1 = abs(w(1, :)' - u1_eksak);
err_w2 = abs(w(2, :)' - u2_eksak);
err_w1_total = sum(err_w1); % norm L1 (taxicab/Manhattan)
err_w2_total = sum(err_w2); % norm L1 (taxicab/Manhattan)
% menampilkan tabel, termasuk error
format long;
disp("Tabel aproksimasi w1,i, solusi eksak u1(t), dan error:");
[t, w(1, :)', u1_eksak, err_w1]
disp("Tabel aproksimasi w2,i, solusi eksak u2(t), dan error:");
[t, w(2, :)', u2_eksak, err_w2]
disp("Error total (norm L1) untuk w1,i:");
disp(err_w1_total);
disp("Error total (norm L1) untuk w2,i:");
disp(err_w2_total);
format;
figure;
hold on;
fplot(sln1, [a,b], 'r');
scatter(t, w(1, :), 'r');
title("u1");
legend("u1 (eksak)", "w1,i (aproksimasi)")
legend('location', 'northwest')
figure;
hold on;
fplot(sln2, [a,b], 'b');
scatter(t, w(2, :), 'b');
title("u2");
legend("u2 (eksak)", "w2,i (aproksimasi)")
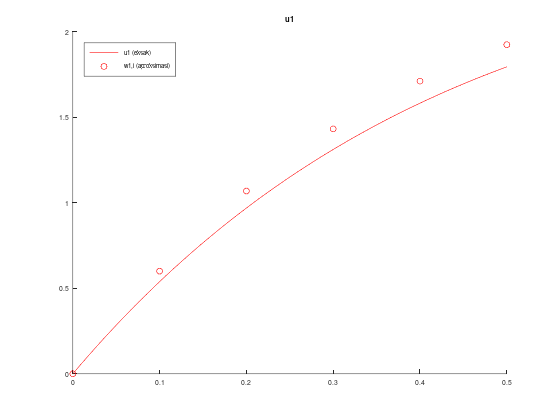
legend('location', 'northwest')Tabel aproksimasi w1,i, solusi eksak u1(t), dan error:
ans =
0 0 0 0
0.100000000000000 0.600000000000000 0.538263906772417 0.061736093227583
0.200000000000000 1.068000000000000 0.968512994104659 0.099487005895341
0.300000000000000 1.430880000000000 1.310736547027331 0.120143452972669
0.400000000000000 1.710124800000000 1.581284350416023 0.128840449583977
0.500000000000000 1.922903808000000 1.793527048067598 0.129376759932402
Tabel aproksimasi w2,i, solusi eksak u2(t), dan error:
ans =
0 0 0 0
0.100000000000000 0.360000000000000 0.319632043667268 0.040367956332732
0.200000000000000 0.633600000000000 0.568791675789742 0.064808324210258
0.300000000000000 0.838656000000000 0.760744801402045 0.077911198597955
0.400000000000000 0.989429760000000 0.906333355910227 0.083096404089773
0.500000000000000 1.097308569600000 1.014415451789714 0.082893117810286
Error total (norm L1) untuk w1,i:
0.539583761611971
Error total (norm L1) untuk w2,i:
0.349077001041004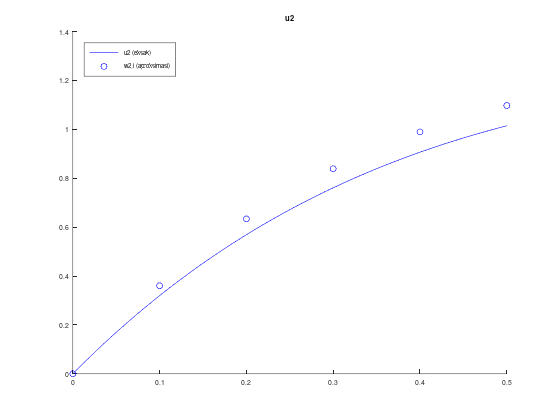
Contoh \(n=4\) (metode Taylor orde 4)
Dengan contoh yang sama,
\[u_1' = f_1(t, u_1, u_2) = -4u_1+3u_2+6\]
\[u_2' = f_2(t, u_1, u_2) = -2.4u_1+1.6u_2+3.6\]
Apabila ingin menggunakan metode Taylor orde 4, kita perlu memiliki turunan (terhadap \(t\)) dari \(f_1\) maupun dari \(f_2\) hingga turunan ketiga (\(n-1=4-1=3\)).
Untuk \(f_1\),
$$\[\begin{align*} f_1(t, u_1, u_2) &= -4u_1 + 3u_2 + 6 \\[1em] f_1'(t, u_1, u_2) &= \frac{d}{dt} f_1(t, u_1, u_2) \\ &= \frac{d}{dt} \left(-4u_1 + 3u_2 + 6\right) \\ &= -4u'_1 + 3u'_2 \\ &= -4\left(-4u_1 + 3u_2 + 6\right) + 3\left(-2.4u_1 + 1.6u_2 + 3.6\right) \\ &= 16u_1 - 12u_2 - 24 - 7.2u_1 + 4.8u_2 + 10.8 \\ &= 8.8u_1 - 7.2u_2 - 13.2 \\[1em] f_1''(t, u_1, u_2) &= \frac{d}{dt} f_1'(t, u_1, u_2) \\ &= \frac{d}{dt} \left(8.8u_1 - 7.2u_2 - 13.2\right) \\ &= 8.8u_1' - 7.2u_2' \\ &= 8.8\left(-4u_1 + 3u_2 + 6\right) - 7.2\left(-2.4u_1 + 1.6u_2 + 3.6\right) \\ &= -35.2u_1 + 26.4u_2 + 52.8 + 17.28u_1 - 11.52u_2 - 25.92 \\ &= -17.92u_1 + 14.88u_2 + 26.8 \\[1em] f_1'''(t, u_1, u_2) &= \frac{d}{dt} f_1''(t, u_1, u_2) \\ &= \frac{d}{dt} \left(-17.92u_1 + 14.88u_2 + 26.8\right) \\ &= -17.92u_1' + 14.88u_2' \\ &= -17.92\left(-4u_1 + 3u_2 + 6\right) + 14.88\left(-2.4u_1 + 1.6u_2 + 3.6\right) \\ &= 71.68u_1 - 53.76u_2 -107.52 - 35.712u_1 + 23.808u_2 + 53.568 \\ &= 35.968u_1 - 29.952u_2 - 53.952 \end{align*}\]$$
Untuk \(f_2\),
$$\[\begin{align*} f_2(t, u_1, u_2) &= -2.4u_1 + 1.6u_2 + 3.6 \\[1em] f_2'(t, u_1, u_2) &= \frac{d}{dt} f_2(t, u_1, u_2) \\ &= \frac{d}{dt} \left(-2.4u_1 + 1.6u_2 + 3.6\right) \\ &= -2.4u_1' + 1.6u_2' \\ &= -2.4\left(-4u_1 + 3u_2 + 6\right) + 1.6\left(-2.4u_1 + 1.6u_2 + 3.6\right) \\ &= 9.6u_1 - 7.2u_2 - 14.4 + -3.84u_1 + 2.56u_2 + 5.76 \\ &= 5.76u_1 - 4.64u_2 - 8.64 \\[1em] f_2''(t, u_1, u_2) &= \frac{d}{dt} f_2'(t, u_1, u_2) \\ &= \frac{d}{dt} \left(5.76u_1 - 4.64u_2 - 8.64\right) \\ &= 5.76u_1' - 4.64u_2' \\ &= 5.76\left(-4u_1 + 3u_2 + 6\right) -4.64\left(-2.4u_1 + 1.6u_2 + 3.6\right) \\ &= -23.04u_1 + 17.28u_2 + 34.56 + 11.136u_1 - 7.424u_2 - 16.704 \\ &= -11.904u_1 + 9.856u_2 + 17.856 \\[1em] f_2'''(t, u_1, u_2) &= \frac{d}{dt} f_2''(t, u_!, u_2) \\ &= \frac{d}{dt} \left(-11.904u_1 + 9.856u_2 + 17.856\right) \\ &= -11.904u_1' + 9.856u_2' \\ &= -11.904\left(-4u_1 + 3u_2 + 6\right) + 9.856\left(-2.4u_1 + 1.6u_2 + 3.6\right) \\ &= 47.616u_1 - 35.712u_2 - 71.424 - 23.6544u_1 + 15.7696u_2 + 35.4816 \\ &= 23.9616u_1 - 19.9424u_2 - 35.9424 \end{align*}\]$$
Sehingga, untuk \(f_1\),
$$\[\begin{align*} f_1(t, u_1, u_2) &= -4u_1 + 3u_2 + 6 \\[1em] f_1'(t, u_1, u_2) &= 8.8u_1 - 7.2u_2 - 13.2 \\[1em] f_1''(t, u_1, u_2) &= -17.92u_1 + 14.88u_2 + 26.8 \\[1em] f_1'''(t, u_1, u_2) &= 35.968u_1 - 29.952u_2 - 53.952 \end{align*}\]$$
dan untuk \(f_2\),
$$\[\begin{align*} f_2(t, u_1, u_2) &= -2.4u_1 + 1.6u_2 + 3.6 \\[1em] f_2'(t, u_1, u_2) &= 5.76u_1 - 4.64u_2 - 8.64 \\[1em] f_2''(t, u_1, u_2) &= -11.904u_1 + 9.856u_2 + 17.856 \\[1em] f_2'''(t, u_1, u_2) &= 23.9616u_1 - 19.9424u_2 - 35.9424 \end{align*}\]$$
Fungsi \(f_1\) dan \(f_2\) serta turunan-turunannya bisa kita gunakan sebagai berikut.
f1 = @(t, u) (-4*u(1) +3*u(2) + 6);
f1p = @(t, u) (8.8*u(1) - 7.2*u(2) - 13.2);
f1pp = @(t, u) (-17.92*u(1) + 14.88*u(2) + 26.8);
f1ppp = @(t, u) (35.968*u(1) - 29.952*u(2) - 53.952);
turunan_f1 = {f1p, f1pp, f1ppp};
f2 = @(t, u) (-2.4*u(1) + 1.6*u(2) + 3.6);
f2p = @(t, u) (5.76*u(1) - 4.64*u(2) - 8.64);
f2pp = @(t, u) (-11.904*u(1) + 9.856*u(2) + 17.856);
f2ppp = @(t, u) (23.9616*u(1) - 19.9424*u(2) - 35.9424);
turunan_f2 = {f2p, f2pp, f2ppp};
a = 0;
b = 0.5;
h = 0.1;
N = (b - a) / h;
alpha1 = 0;
alpha2 = 0;
[t, w] = taylor_sysm({f1, f2}, {turunan_f1, turunan_f2}, a, b, N, [alpha1, alpha2]);
sln1 = @(t) (-3.375*exp(-2*t) + 1.875*exp(-0.4*t) + 1.5);
sln2 = @(t) (-2.25*exp(-2*t) + 2.25*exp(-0.4*t));
u1_eksak = sln1(t);
u2_eksak = sln2(t);
% menghitung error
err_w1 = abs(w(1, :)' - u1_eksak);
err_w2 = abs(w(2, :)' - u2_eksak);
err_w1_total = sum(err_w1); % norm L1 (taxicab/Manhattan)
err_w2_total = sum(err_w2); % norm L1 (taxicab/Manhattan)
% menampilkan tabel, termasuk error
format long;
disp("Tabel aproksimasi w1,i, solusi eksak u1(t), dan error:");
[t, w(1, :)', u1_eksak, err_w1]
disp("Tabel aproksimasi w2,i, solusi eksak u2(t), dan error:");
[t, w(2, :)', u2_eksak, err_w2]
disp("Error total (norm L1) untuk w1,i:");
disp(err_w1_total);
disp("Error total (norm L1) untuk w2,i:");
disp(err_w2_total);
format;
figure;
hold on;
fplot(sln1, [a,b], 'r');
scatter(t, w(1, :), 'r');
title("u1");
legend("u1 (eksak)", "w1,i (aproksimasi)")
legend('location', 'northwest')
figure;
hold on;
fplot(sln2, [a,b], 'b');
scatter(t, w(2, :), 'b');
title("u2");
legend("u2 (eksak)", "w2,i (aproksimasi)")
legend('location', 'northwest')Tabel aproksimasi w1,i, solusi eksak u1(t), dan error:
ans =
0 0 0 0
0.100000000000000 0.538241866666667 0.538263906772417 0.000022040105751
0.200000000000000 0.968476855353088 0.968512994104659 0.000036138751571
0.300000000000000 1.310692432573591 1.310736547027331 0.000044114453740
0.400000000000000 1.581236949834047 1.581284350416023 0.000047400581977
0.500000000000000 1.793479923348867 1.793527048067598 0.000047124718731
Tabel aproksimasi w2,i, solusi eksak u2(t), dan error:
ans =
0 0 0 0
0.100000000000000 0.319626240000000 0.319632043667268 0.000005803667268
0.200000000000000 0.568785014157039 0.568791675789742 0.000006661632703
0.300000000000000 0.760741028831847 0.760744801402045 0.000003772570198
0.400000000000000 0.906335276984882 0.906333355910227 0.000001921074655
0.500000000000000 1.014425131989109 1.014415451789714 0.000009680199395
Error total (norm L1) untuk w1,i:
1.968186117699000e-04
Error total (norm L1) untuk w2,i:
2.783914421899958e-05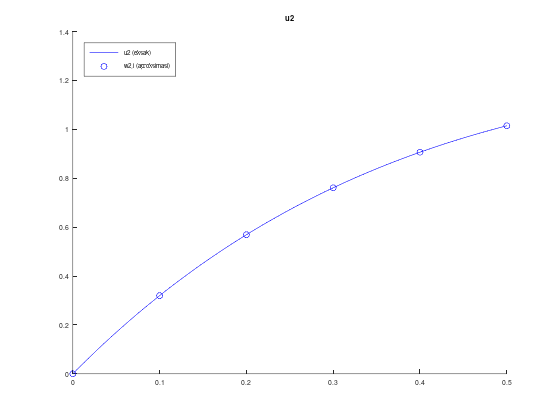
Contoh lain: untuk metode Adams predictor-corrector orde 4
function [t, w] = adams_pc_orde4_sysm(cell_f, a, b, N, alphas)
m = length(cell_f);
% Inisiasi variabel awal
h = (b - a) / N;
t = zeros(N + 1, 1);
w = zeros(m, N + 1);
t(1) = a;
w(:, 1) = alphas;
% Hitung w(2), w(3), w(4) menggunakan metode Runge-Kutta orde 4
k1 = zeros(m, 1);
k2 = zeros(m, 1);
k3 = zeros(m, 1);
k4 = zeros(m, 1);
for i = 1 : 3
t(i + 1) = t(i) + h;
for j = 1 : m
k1(j) = h * cell_f{j}(t(i), w(:,i));
endfor
for j = 1 : m
k2(j) = h * cell_f{j}(t(i) + (h/2), w(:,i) + (k1/2));
endfor
for j = 1 : m
k3(j) = h * cell_f{j}(t(i) + (h/2), w(:,i) + (k2/2));
endfor
for j = 1 : m
k4(j) = h * cell_f{j}(t(i + 1), w(:,i) + k3);
endfor
for j = 1 : m
w(j,i+1) = w(j,i) + (k1(j) + 2*k2(j) + 2*k3(j) + k4(j)) / 6;
endfor
endfor
% Algoritma utama Adams Predictor-Corrector orde 4
m0 = zeros(m, 1);
m1 = zeros(m, 1);
m2 = zeros(m, 1);
m3 = zeros(m, 1);
m4 = zeros(m, 1);
for i = 4 : N
t(i + 1) = t(i) + h;
for j = 1 : m
m1(j) = cell_f{j}(t(i), w(:,i));
endfor
for j = 1 : m
m2(j) = cell_f{j}(t(i-1), w(:,i-1));
endfor
for j = 1 : m
m3(j) = cell_f{j}(t(i-2), w(:,i-2));
endfor
for j = 1 : m
m4(j) = cell_f{j}(t(i-3), w(:,i-3));
endfor
% Adams-Bashforth orde 4 (four-step)
for j = 1 : m
w(j,i+1) = w(j,i) + (h/24) * (55*m1(j) - 59*m2(j) + 37*m3(j) - 9*m4(j));
endfor
% Adams-Moulton orde 4 (three-step)
for j = 1 : m
m0(j) = cell_f{j}(t(i+1), w(:,i+1));
endfor
for j = 1 : m
w(j,i+1) = w(j,i) + (h/24) * (9*m0(j) + 19*m1(j) - 5*m2(j) + m3(j));
endfor
endfor
endfunctionMencoba untuk masalah yang sama, yaitu
\(u'_1 = -4u_1+3u_2+6, \;u_1(0)=0\)
\(u'_2 = -2.4u_1+1.6u_2+3.6, \;u_2(0)=0\)
Akan diuji dengan \(h=0.1\) dan \(0\leq t \leq 0.5\)
Solusi eksak:
\(u_1(t)=-3.375e^{-2t}+1.875e^{-0.4t}+1.5\)
\(u_2(t) = -2.25e^{-2t}+2.25e^{-0.4t}\)
f1 = @(t, u) (-4*u(1) +3*u(2) + 6);
f2 = @(t, u) (-2.4*u(1) + 1.6*u(2) + 3.6);
a = 0;
b = 0.5;
h = 0.1;
N = (b - a) / h;
alpha1 = 0;
alpha2 = 0;
[t, w] = adams_pc_orde4_sysm({f1, f2}, a, b, N, [alpha1, alpha2]);
sln1 = @(t) (-3.375*exp(-2*t) + 1.875*exp(-0.4*t) + 1.5);
sln2 = @(t) (-2.25*exp(-2*t) + 2.25*exp(-0.4*t));
u1_eksak = sln1(t);
u2_eksak = sln2(t);
% menghitung error
err_w1 = abs(w(1, :)' - u1_eksak);
err_w2 = abs(w(2, :)' - u2_eksak);
err_w1_total = sum(err_w1); % norm L1 (taxicab/Manhattan)
err_w2_total = sum(err_w2); % norm L1 (taxicab/Manhattan)
% menampilkan tabel, termasuk error
format long;
disp("Tabel aproksimasi w1,i, solusi eksak u1(t), dan error:");
[t, w(1, :)', u1_eksak, err_w1]
disp("Tabel aproksimasi w2,i, solusi eksak u2(t), dan error:");
[t, w(2, :)', u2_eksak, err_w2]
disp("Error total (norm L1) untuk w1,i:");
disp(err_w1_total);
disp("Error total (norm L1) untuk w2,i:");
disp(err_w2_total);
format;
figure;
hold on;
fplot(sln1, [a,b], 'r');
scatter(t, w(1, :), 'r');
title("u1");
legend("u1 (eksak)", "w1,i (aproksimasi)")
legend('location', 'northwest')
figure;
hold on;
fplot(sln2, [a,b], 'b');
scatter(t, w(2, :), 'b');
title("u2");
legend("u2 (eksak)", "w2,i (aproksimasi)")
legend('location', 'northwest')Tabel aproksimasi w1,i, solusi eksak u1(t), dan error:
ans =
0 0 0 0
0.100000000000000 0.538255200000000 0.538263906772417 0.000008706772417
0.200000000000000 0.968498737529088 0.968512994104659 0.000014256575571
0.300000000000000 1.310719039205257 1.310736547027331 0.000017507822074
0.400000000000000 1.581306013228106 1.581284350416023 0.000021662812083
0.500000000000000 1.793573533217050 1.793527048067598 0.000046485149452
Tabel aproksimasi w2,i, solusi eksak u2(t), dan error:
ans =
0 0 0 0
0.100000000000000 0.319626240000000 0.319632043667268 0.000005803667268
0.200000000000000 0.568782173034906 0.568791675789742 0.000009502754836
0.300000000000000 0.760733131868175 0.760744801402045 0.000011669533870
0.400000000000000 0.906347797116244 0.906333355910227 0.000014441206017
0.500000000000000 1.014446438459705 1.014415451789714 0.000030986669992
Error total (norm L1) untuk w1,i:
1.086191315975427e-04
Error total (norm L1) untuk w2,i:
7.240383198242606e-05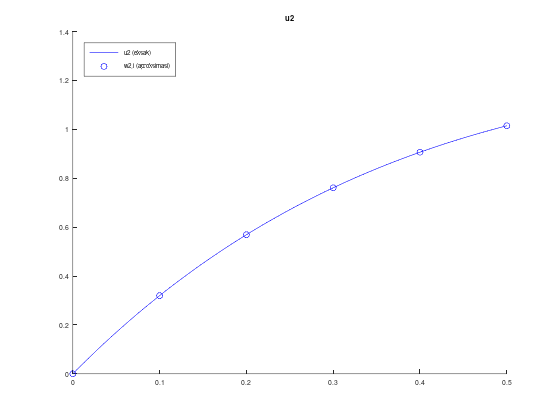
PDB orde tinggi
(penjelasan tanpa kode) Mengubah PDB orde tinggi menjadi sistem PDB orde 1
Misalkan ada PDB orde \(m\) (tidak harus linier),
\[\dots y^{\left(m\right)}\left(t\right) + \dots y^{\left(m-1\right)}\left(t\right) + \dots + \dots y''\left(t\right) + \dots y'\left(t\right) + \dots y\left(t\right) + \dots = 0\]
yang bisa dipindah ruas dsb, untuk memperoleh bentuk:
\[y^{\left(m\right)}\left(t\right) = \left[\text{sisanya}\right]\]
atau biasa ditulis
\[y^{\left(m\right)}\left(t\right) = f\left(t, y, y', y'', \dots, y^{\left(m-1\right)}\right)\]
Kita bisa mendefinisikan fungsi \(u_1 \left(t\right), u_2 \left(t\right), \dots, u_m \left(t\right)\) sebagai berikut,
\[\begin{align*} u_1 \left(t\right) &= y\left(t\right) \\ u_2 \left(t\right) &= y'\left(t\right) \\ &\vdots \\ u_j \left(t\right) &= y^{\left(j-1\right)}\left(t\right) \\ &\vdots \\ u_{m-1} \left(t\right) &= y^{\left(m-2\right)}\left(t\right) \\ u_m \left(t\right) &= y^{\left(m-1\right)}\left(t\right) \end{align*}\]
Sehingga turunannya terhadap \(t\) adalah,
\[\begin{align*} \frac{du_1}{dt} &= y'\left(t\right) \\ \frac{du_2}{dt} &= y''\left(t\right) \\ &\vdots \\ \frac{du_j}{dt} &= y^{\left(j\right)}\left(t\right) \\ &\vdots \\ \frac{du_{m-1}}{dt} &= y^{\left(m-1\right)}\left(t\right) \\ \frac{du_m}{dt} &= y^{\left(m\right)}\left(t\right) \end{align*}\]
Ternyata, \(u_1'\left(t\right) = y'\left(t\right) = u_2\left(t\right)\), lalu \(u_2'\left(t\right) = y''\left(t\right) = u_3\left(t\right)\), dan seterusnya. Untuk yang terakhir, sebelumnya kita sudah menuliskan
\[y^{\left(m\right)}\left(t\right) = f\left(t, y, y', y'', \dots, y^{\left(m-1\right)}\right)\]
sedangkan \(\frac{du_m}{dt} = y^{\left(m\right)}\left(t\right)\).
Sehingga, bisa ditulis:
\[\begin{align*} \frac{du_1}{dt} &= u_2\left(t\right) \\ \frac{du_2}{dt} &= u_3\left(t\right) \\ &\vdots \\ \frac{du_j}{dt} &= u_{j+1}\left(t\right) \\ &\vdots \\ \frac{du_{m-1}}{dt} &= u_m\left(t\right) \\ \frac{du_m}{dt} &= f\left(t, y, y', y'', \dots, y^{\left(m-1\right)}\right) \\ \end{align*}\]
yaitu sistem PDB orde 1 dalam \(u_1 \left(t\right), u_2 \left(t\right), \dots, u_m \left(t\right)\).
Solusi \(y\left(t\right)\) bisa diperoleh dari \(u_1 \left(t\right)\). Apabila ditanya \(y'\left(t\right)\), maka bisa diperoleh dari \(u_2 \left(t\right)\). Apabila ditanya \(y''\left(t\right)\), maka bisa diperoleh dari \(u_3 \left(t\right)\), dan seterusnya.
Contoh: mengubah PDB orde 3 menjadi sistem PDB
Menggunakan soal Exercise Set 5.9 no. 3d dari buku,
\[t^3 y''' - t^2 y'' + 3ty' - 4y = 5t^3 \ln{t} + 9t^3, \quad 1 \le t \le 2\]
\[y(1) = 0, \quad y'(1) = 1, \quad y''(1) = 3\]
dengan \(h=0.1\), dan diketahui solusi eksak
\[y(t) = -t^2 + t\cos{\left(\ln{t}\right)} + t\sin{\left(\ln{t}\right)} + t^3 \ln{t}\]
\[y'(t) = -2t + 2\cos{\left(\ln{t}\right)} + t^2 + 3t^2 \ln{t}\]
\[y''(t) = -2 - \frac{2}{t}\sin{\left(\ln{t}\right)} + 5t + 6t \ln{t}\]
Perhatikan bahwa turunan tertinggi adalah turunan ketiga, sehingga PDB yang diberikan adalah PDB orde 3, yaitu PDB orde \(m\) dengan \(m=3\).
Kita bisa melakukan pindah ruas agar memperoleh bentuk
\[y''' = \left[\text{sisanya}\right]\]
atau bisa ditulis
\[y''' = f\left(t, y, y', y''\right)\]
seperti berikut:
\[t^3 y''' - t^2 y'' + 3ty' - 4y = 5t^3 \ln{t} + 9t^3\]
\[t^3 y''' = t^2 y'' - 3ty' + 4y + 5t^3 \ln{t} + 9t^3\]
\[y''' = \frac{1}{t^3}\left(t^2 y'' - 3ty' + 4y + 5t^3 \ln{t} + 9t^3\right)\]
\[y''' = \frac{1}{t} y'' - \frac{3}{t^2}y' + \frac{4}{t^3}y + 5 \ln{t} + 9\]
Sehingga bisa ditulis
\[y''' = f\left(t, y, y', y''\right) = \frac{1}{t} y'' - \frac{3}{t^2}y' + \frac{4}{t^3}y + 5 \ln{t} + 9, \quad 1 \le t \le 2\]
\[y(1) = 0, \quad y'(1) = 1, \quad y''(1) = 3\]
PDB orde \(m=3\) bisa diubah menjadi sistem PDB orde 1 yang terdiri dari \(m=3\) persamaan, dengan permisalan
\[u_1(t) = y(t)\]
\[u_2(t) = y'(t)\]
\[u_3(t) = y''(t)\]
sehingga
\[\begin{align*} u_1'(t) &= y'(t) = u_2(t) \\ u_2'(t) &= y''(t) = u_3(t) \\ u_3'(t) &= y'''(t) = f\left(t, y, y', y''\right) = \frac{1}{t} y'' - \frac{3}{t^2}y' + \frac{4}{t^3}y + 5 \ln{t} + 9 \end{align*}\]
atau bisa ditulis
\[\begin{align*} u_1'(t) &= u_2(t) \\ u_2'(t) &= u_3(t) \\ u_3'(t) &= f\left(t, u_1, u_2, u_3\right) = \frac{1}{t} u_3(t) - \frac{3}{t^2}u_2(t) + \frac{4}{t^3}u_1(t) + 5 \ln{t} + 9 \end{align*}\]
Berdasarkan permisalan, nilai-nilai awal
\[y(1) = 0, \quad y'(1) = 1, \quad y''(1) = 3\]
menjadi
\[u_1(1) = 0, \quad u_2(1) = 1, \quad u_3(1) = 3\]
Sehingga, diperoleh sistem PDB orde 3 sebagai berikut:
\[\begin{align*} u_1' &= u_2, \quad u_1(1) = 0 \\ u_2' &= u_3, \quad u_2(1) = 1 \\ u_3' &= \frac{1}{t} u_3 - \frac{3}{t^2}u_2 + \frac{4}{t^3}u_1 + 5 \ln{t} + 9, \quad u_3(1) = 3 \end{align*}\]
Kita dapat memisalkan
\[\begin{align*} f_1\left(t, u_1, u_2, u_3\right) &= u_1' \\ f_2\left(t, u_1, u_2, u_3\right) &= u_2' \\ f_3\left(t, u_1, u_2, u_3\right) &= u_3' \end{align*}\]
yaitu
\[\begin{align*} f_1\left(t, u_1, u_2, u_3\right) &= u_2 \\ f_2\left(t, u_1, u_2, u_3\right) &= u_3 \\ f_3\left(t, u_1, u_2, u_3\right) &= \frac{1}{t} u_3 - \frac{3}{t^2}u_2 + \frac{4}{t^3}u_1 + 5 \ln{t} + 9 \end{align*}\]
agar sistem PDB orde 3 di atas bisa ditulis dalam bentuk umum sistem PDB orde 1, yaitu
\[\begin{align*} u_1' &= f_1\left(t, u_1, u_2, u_3\right) \\ u_2' &= f_2\left(t, u_1, u_2, u_3\right) \\ u_3' &= f_3\left(t, u_1, u_2, u_3\right) \end{align*}\]
masih dengan nilai-nilai awal
\[u_1(1) = 0, \quad u_2(1) = 1, \quad u_3(1) = 3\]
Setelah bentuknya diubah menjadi sistem PDB orde 1, kita dapat menyelesaikannya menggunakan algoritma-algoritma sistem PDB orde 1 seperti biasa. Berdasarkan permisalan yang telah dilakukan,
solusi \(u_1(t)\) akan menjadi solusi \(y(t)\), biasanya ini yang diminta
solusi \(u_2(t)\) akan menjadi solusi \(y'(t)\)
solusi \(u_3(t)\) akan menjadi solusi \(y''(t)\)
Walaupun mungkin kita hanya memerlukan solusi \(y(t)\), algoritma yang tersedia mengharuskan semua nilai dihitung di tiap iterasi. Tidak ada salahnya juga; siapa tahu, misalnya solusi \(y'(t)\) atau solusi \(y''(t)\) diperlukan nantinya.
(Apabila diperlukan, nilai \(y^{\left(m\right)}(t)\), yaitu nilai \(y'''(t)\), bisa dihitung menggunakan \(f\left(t, y, y', y'', \dots, y^{\left(m-1\right)}\right)\), yaitu menggunakan \(f\left(t, y, y', y''\right) = \frac{1}{t} y'' - \frac{3}{t^2}y' + \frac{4}{t^3}y + 5 \ln{t} + 9\).)
Contoh metode Runge-Kutta orde 4
Sistem kita adalah
\[\begin{align*} u_1' &= f_1\left(t, u_1, u_2, u_3\right) = u_2 \\ u_2' &= f_2\left(t, u_1, u_2, u_3\right) = u_3 \\ u_3' &= f_3\left(t, u_1, u_2, u_3\right) = \frac{1}{t} u_3 - \frac{3}{t^2}u_2 + \frac{4}{t^3}u_1 + 5 \ln{t} + 9 \end{align*}\]
\[1 \le t \le 2\]
\[u_1(1) = 0, \quad u_2(1) = 1, \quad u_3(1) = 3\]
dengan \(h=0.1\), dan diketahui solusi eksak
\[y(t) = -t^2 + t\cos{\left(\ln{t}\right)} + t\sin{\left(\ln{t}\right)} + t^3 \ln{t}\]
\[y'(t) = -2t + 2\cos{\left(\ln{t}\right)} + t^2 + 3t^2 \ln{t}\]
\[y''(t) = -2 - \frac{2}{t}\sin{\left(\ln{t}\right)} + 5t + 6t \ln{t}\]
(yang bisa dianggap solusi eksak untuk \(u_1\), \(u_2\), dan \(u_3\), sesuai permisalan)
Kita bisa menggunakan metode Runge-Kutta orde 4 untuk sistem, seperti berikut.
f1 = @(t, u) u(2);
f2 = @(t, u) u(3);
f3 = @(t, u) (1/t .* u(3) - 3/(t.^2) .* u(2) + 4/(t.^3) .* u(1) + 5*log(t) + 9);
a = 1;
b = 2;
h = 0.1;
N = (b - a) / h;
alpha1 = 0;
alpha2 = 1;
alpha3 = 3;
[t, w] = rko4_sysm({f1, f2, f3}, a, b, N, [alpha1, alpha2, alpha3]);
% solusi eksak
sln1 = @(t) (-t.^2 + t .* cos(log(t)) + t .* sin(log(t)) + t.^3 .* log(t));
sln2 = @(t) (-2*t + 2 * cos(log(t)) + t.^2 + 3 * t.^2 .* log(t));
sln3 = @(t) (-2 - 2./t .* sin(log(t)) + 5*t + 6 * t .* log(t));
u1_eksak = sln1(t);
u2_eksak = sln2(t);
u3_eksak = sln3(t);
[t, w', u1_eksak, u2_eksak, u3_eksak]
figure;
hold on;
fplot(sln1, [a, b], 'r');
scatter(t, w(1, :), 'r'); % ambil baris pertama yaitu solusi u1
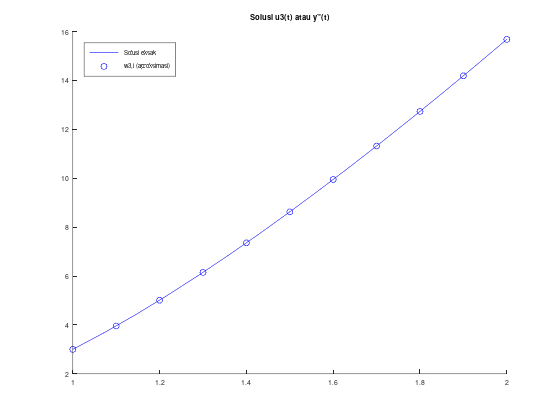
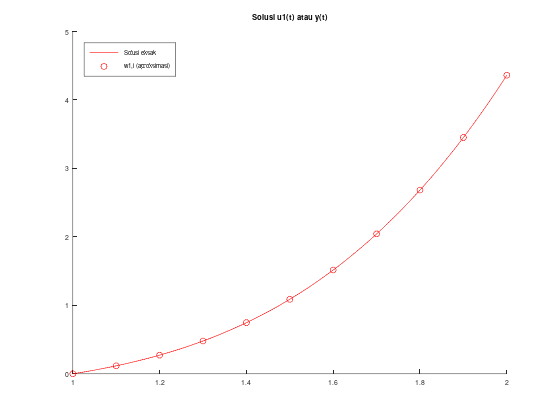
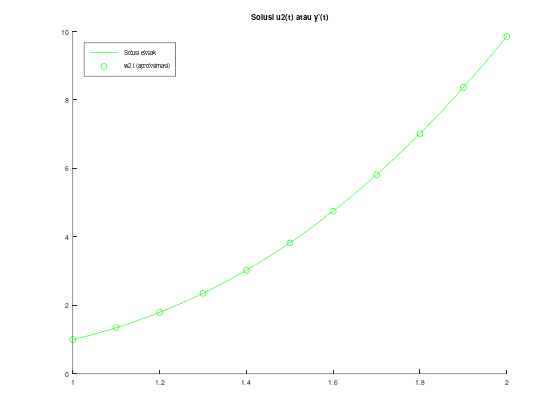
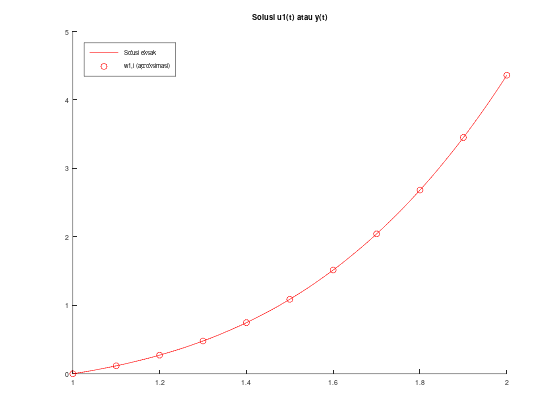
title("Solusi u1(t) atau y(t)");
legend("Solusi eksak", "w1,i (aproksimasi)");
legend('location', 'northwest');
figure;
hold on;
fplot(sln2, [a, b], 'g');
scatter(t, w(2, :), 'g'); % ambil baris kedua yaitu solusi u2
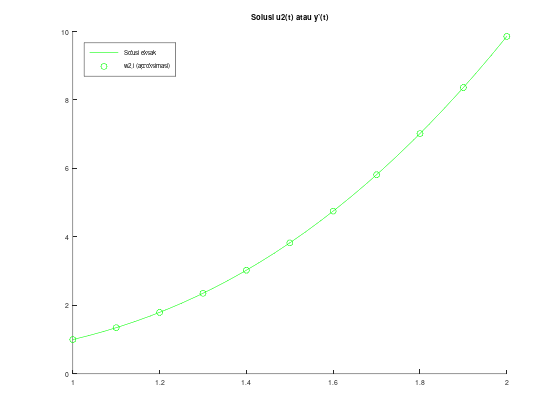
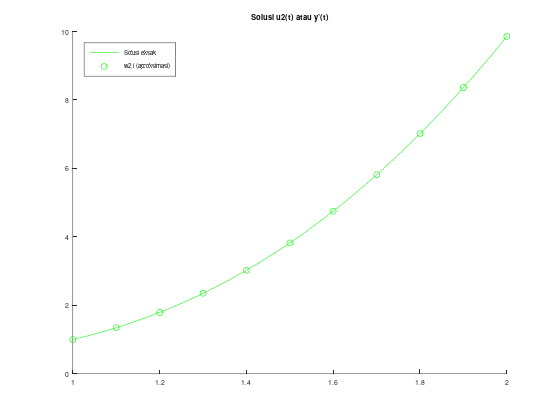
title("Solusi u2(t) atau y'(t)");
legend("Solusi eksak", "w2,i (aproksimasi)");
legend('location', 'northwest');
figure;
hold on;
fplot(sln3, [a, b], 'b');
scatter(t, w(3, :), 'b'); % ambil baris ketiga yaitu solusi u3
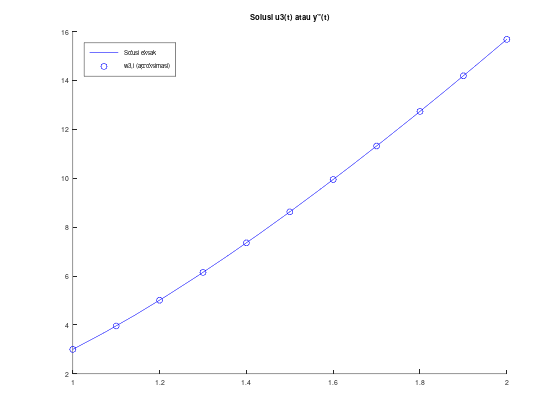
title("Solusi u3(t) atau y''(t)");
legend("Solusi eksak", "w3,i (aproksimasi)");
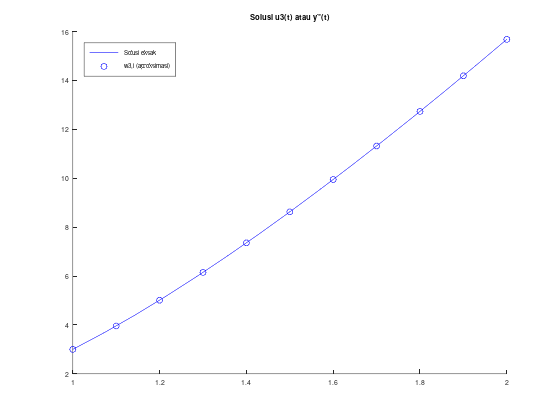
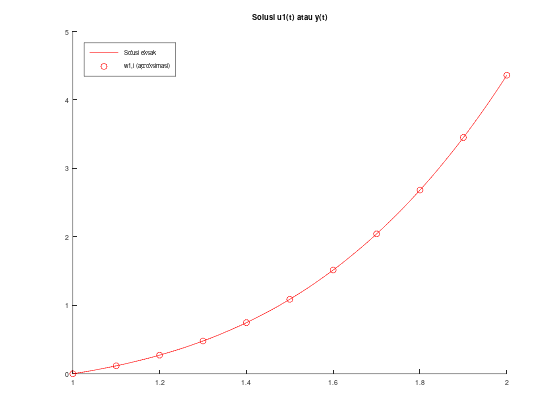
legend('location', 'northwest');ans =
1.0000 0 1.0000 3.0000 0 1.0000 3.0000
1.1000 0.1165 1.3469 3.9560 0.1165 1.3469 3.9560
1.2000 0.2727 1.7945 5.0105 0.2727 1.7945 5.0105
1.3000 0.4791 2.3517 6.1474 0.4791 2.3517 6.1474
1.4000 0.7470 3.0263 7.3547 0.7470 3.0263 7.3547
1.5000 1.0885 3.8247 8.6232 1.0885 3.8247 8.6233
1.6000 1.5163 4.7527 9.9459 1.5163 4.7528 9.9459
1.7000 2.0435 5.8155 11.3170 2.0435 5.8155 11.3170
1.8000 2.6840 7.0176 12.7319 2.6840 7.0176 12.7320
1.9000 3.4518 8.3632 14.1869 3.4518 8.3633 14.1869
2.0000 4.3616 9.8562 15.6788 4.3616 9.8562 15.6788
Apabila perlu dihitung errornya, kodenya bisa menjadi seperti berikut:
f1 = @(t, u) u(2);
f2 = @(t, u) u(3);
f3 = @(t, u) (1/t .* u(3) - 3/(t.^2) .* u(2) + 4/(t.^3) .* u(1) + 5*log(t) + 9);
a = 1;
b = 2;
h = 0.1;
N = (b - a) / h;
alpha1 = 0;
alpha2 = 1;
alpha3 = 3;
[t, w] = rko4_sysm({f1, f2, f3}, a, b, N, [alpha1, alpha2, alpha3]);
% solusi eksak
sln1 = @(t) (-t.^2 + t .* cos(log(t)) + t .* sin(log(t)) + t.^3 .* log(t));
sln2 = @(t) (-2*t + 2 * cos(log(t)) + t.^2 + 3 * t.^2 .* log(t));
sln3 = @(t) (-2 - 2./t .* sin(log(t)) + 5*t + 6 * t .* log(t));
u1_eksak = sln1(t);
u2_eksak = sln2(t);
u3_eksak = sln3(t);
% menghitung error
err_w1 = abs(w(1, :)' - u1_eksak);
err_w2 = abs(w(2, :)' - u2_eksak);
err_w3 = abs(w(3, :)' - u3_eksak);
err_w1_total = sum(err_w1); % norm L1 (taxicab/Manhattan)
err_w2_total = sum(err_w2); % norm L1 (taxicab/Manhattan)
err_w3_total = sum(err_w3); % norm L1 (taxicab/Manhattan)
% menampilkan tabel, termasuk error
format long;
disp("Tabel aproksimasi w1,i, solusi eksak u1(t), dan error:");
[t, w(1, :)', u1_eksak, err_w1]
disp("Tabel aproksimasi w2,i, solusi eksak u2(t), dan error:");
[t, w(2, :)', u2_eksak, err_w2]
disp("Tabel aproksimasi w3,i, solusi eksak u3(t), dan error:");
[t, w(3, :)', u3_eksak, err_w3]
disp("Error total (norm L1) untuk w1,i:");
disp(err_w1_total);
disp("Error total (norm L1) untuk w2,i:");
disp(err_w2_total);
disp("Error total (norm L1) untuk w3,i:");
disp(err_w3_total);
format;
figure;
hold on;
fplot(sln1, [a, b], 'r');
scatter(t, w(1, :), 'r'); % ambil baris pertama yaitu solusi u1
title("Solusi u1(t) atau y(t)");
legend("Solusi eksak", "w1,i (aproksimasi)");
legend('location', 'northwest');
figure;
hold on;
fplot(sln2, [a, b], 'g');
scatter(t, w(2, :), 'g'); % ambil baris kedua yaitu solusi u2
title("Solusi u2(t) atau y'(t)");
legend("Solusi eksak", "w2,i (aproksimasi)");
legend('location', 'northwest');
figure;
hold on;
fplot(sln3, [a, b], 'b');
scatter(t, w(3, :), 'b'); % ambil baris ketiga yaitu solusi u3
title("Solusi u3(t) atau y''(t)");
legend("Solusi eksak", "w3,i (aproksimasi)");
legend('location', 'northwest');Tabel aproksimasi w1,i, solusi eksak u1(t), dan error:
ans =
1.000000000000000 0 0 0
1.100000000000000 0.116547765077132 0.116547953377741 0.000000188300609
1.200000000000000 0.272737593417178 0.272737913137213 0.000000319720036
1.300000000000000 0.479101055922200 0.479101624357037 0.000000568434836
1.400000000000000 0.746997034090164 0.746998073629463 0.000001039539299
1.500000000000000 1.088490794798314 1.088492594095847 0.000001799297533
1.600000000000001 1.516261839314915 1.516264730431065 0.000002891116151
1.700000000000001 2.043532071845456 2.043536416215900 0.000004344370444
1.800000000000001 2.684008671952472 2.684014851438298 0.000006179485825
1.900000000000001 3.451837841224076 3.451846252199066 0.000008410974990
2.000000000000001 4.361566750517713 4.361577799834785 0.000011049317072
Tabel aproksimasi w2,i, solusi eksak u2(t), dan error:
ans =
1.000000000000000 1.000000000000000 1.000000000000000 0
1.100000000000000 1.346897244698541 1.346898796867440 0.000001552168898
1.200000000000000 1.794476400848503 1.794479954480695 0.000003553632192
1.300000000000000 2.351739790653634 2.351745763551004 0.000005972897370
1.400000000000000 3.026298521404629 3.026307271933378 0.000008750528749
1.500000000000000 3.824715727217527 3.824727552609112 0.000011825391586
1.600000000000001 4.752746018651163 4.752761161714929 0.000015143063766
1.700000000000001 5.815506875823461 5.815525533513762 0.000018657690301
1.800000000000001 7.017604163612482 7.017626495142349 0.000022331529867
1.900000000000001 8.363225949009005 8.363252082824820 0.000026133815815
2.000000000000001 9.856213929909213 9.856243969447302 0.000030039538089
Tabel aproksimasi w3,i, solusi eksak u3(t), dan error:
ans =
Columns 1 through 3:
1.000000000000000e+00 3.000000000000000e+00 3.000000000000000e+00
1.100000000000000e+00 3.956010469157951e+00 3.956018195368995e+00
1.200000000000000e+00 5.010512494112985e+00 5.010526645695958e+00
1.300000000000000e+00 6.147399365577646e+00 6.147418750933507e+00
1.400000000000000e+00 7.354687155068509e+00 7.354710775454516e+00
1.500000000000000e+00 8.623230661511867e+00 8.623257706687671e+00
1.600000000000001e+00 9.945893119295571e+00 9.945922939388453e+00
1.700000000000001e+00 1.131699337911594e+01 1.131702545393904e+01
1.800000000000001e+00 1.273192816711290e+01 1.273196207929798e+01
1.900000000000001e+00 1.418690793287085e+01 1.418694334605300e+01
2.000000000000001e+00 1.567876824876296e+01 1.567880489040572e+01
Column 4:
0
7.726211044278841e-06
1.415158297302099e-05
1.938535586099022e-05
2.362038600622896e-05
2.704517580376375e-05
2.982009288210463e-05
3.207482310685350e-05
3.391218507609040e-05
3.541318215205536e-05
3.664164275640758e-05
Error total (norm L1) untuk w1,i:
3.679055679502163e-05
Error total (norm L1) untuk w2,i:
1.439602566337683e-04
Error total (norm L1) untuk w3,i:
2.597906376617942e-04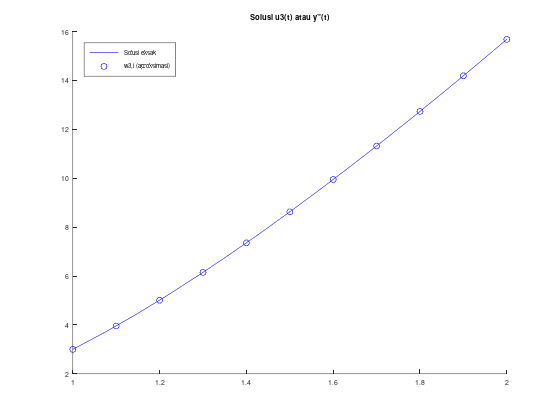
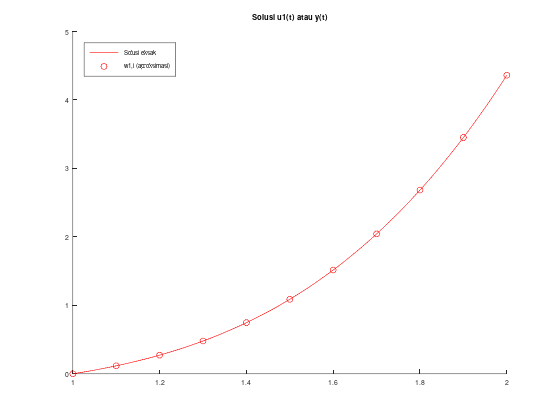
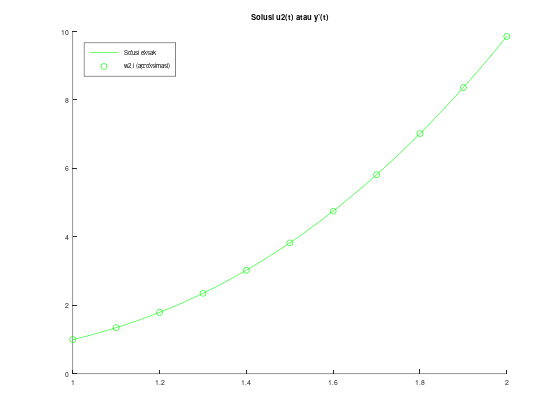
Contoh metode Adams Predictor-Corrector orde 4
Kita bisa menggunakan kode di atas, tinggal menukar fungsi rko4_sysm dengan adams_pc_orde4_sysm
f1 = @(t, u) u(2);
f2 = @(t, u) u(3);
f3 = @(t, u) (1/t .* u(3) - 3/(t.^2) .* u(2) + 4/(t.^3) .* u(1) + 5*log(t) + 9);
a = 1;
b = 2;
h = 0.1;
N = (b - a) / h;
alpha1 = 0;
alpha2 = 1;
alpha3 = 3;
[t, w] = adams_pc_orde4_sysm({f1, f2, f3}, a, b, N, [alpha1, alpha2, alpha3]);
% solusi eksak
sln1 = @(t) (-t.^2 + t .* cos(log(t)) + t .* sin(log(t)) + t.^3 .* log(t));
sln2 = @(t) (-2*t + 2 * cos(log(t)) + t.^2 + 3 * t.^2 .* log(t));
sln3 = @(t) (-2 - 2./t .* sin(log(t)) + 5*t + 6 * t .* log(t));
u1_eksak = sln1(t);
u2_eksak = sln2(t);
u3_eksak = sln3(t);
[t, w', u1_eksak, u2_eksak, u3_eksak]
figure;
hold on;
fplot(sln1, [a, b], 'r');
scatter(t, w(1, :), 'r'); % ambil baris pertama yaitu solusi u1
title("Solusi u1(t) atau y(t)");
legend("Solusi eksak", "w1,i (aproksimasi)");
legend('location', 'northwest');
figure;
hold on;
fplot(sln2, [a, b], 'g');
scatter(t, w(2, :), 'g'); % ambil baris kedua yaitu solusi u2
title("Solusi u2(t) atau y'(t)");
legend("Solusi eksak", "w2,i (aproksimasi)");
legend('location', 'northwest');
figure;
hold on;
fplot(sln3, [a, b], 'b');
scatter(t, w(3, :), 'b'); % ambil baris ketiga yaitu solusi u3
title("Solusi u3(t) atau y''(t)");
legend("Solusi eksak", "w3,i (aproksimasi)");
legend('location', 'northwest');ans =
1.0000 0 1.0000 3.0000 0 1.0000 3.0000
1.1000 0.1165 1.3469 3.9560 0.1165 1.3469 3.9560
1.2000 0.2727 1.7945 5.0105 0.2727 1.7945 5.0105
1.3000 0.4791 2.3517 6.1474 0.4791 2.3517 6.1474
1.4000 0.7470 3.0263 7.3547 0.7470 3.0263 7.3547
1.5000 1.0885 3.8248 8.6232 1.0885 3.8247 8.6233
1.6000 1.5163 4.7528 9.9459 1.5163 4.7528 9.9459
1.7000 2.0435 5.8156 11.3170 2.0435 5.8155 11.3170
1.8000 2.6840 7.0177 12.7319 2.6840 7.0176 12.7320
1.9000 3.4518 8.3633 14.1869 3.4518 8.3633 14.1869
2.0000 4.3616 9.8563 15.6787 4.3616 9.8562 15.6788
Apabila perlu dihitung errornya:
f1 = @(t, u) u(2);
f2 = @(t, u) u(3);
f3 = @(t, u) (1/t .* u(3) - 3/(t.^2) .* u(2) + 4/(t.^3) .* u(1) + 5*log(t) + 9);
a = 1;
b = 2;
h = 0.1;
N = (b - a) / h;
alpha1 = 0;
alpha2 = 1;
alpha3 = 3;
[t, w] = adams_pc_orde4_sysm({f1, f2, f3}, a, b, N, [alpha1, alpha2, alpha3]);
% solusi eksak
sln1 = @(t) (-t.^2 + t .* cos(log(t)) + t .* sin(log(t)) + t.^3 .* log(t));
sln2 = @(t) (-2*t + 2 * cos(log(t)) + t.^2 + 3 * t.^2 .* log(t));
sln3 = @(t) (-2 - 2./t .* sin(log(t)) + 5*t + 6 * t .* log(t));
u1_eksak = sln1(t);
u2_eksak = sln2(t);
u3_eksak = sln3(t);
% menghitung error
err_w1 = abs(w(1, :)' - u1_eksak);
err_w2 = abs(w(2, :)' - u2_eksak);
err_w3 = abs(w(3, :)' - u3_eksak);
err_w1_total = sum(err_w1); % norm L1 (taxicab/Manhattan)
err_w2_total = sum(err_w2); % norm L1 (taxicab/Manhattan)
err_w3_total = sum(err_w3); % norm L1 (taxicab/Manhattan)
% menampilkan tabel, termasuk error
format long;
disp("Tabel aproksimasi w1,i, solusi eksak u1(t), dan error:");
[t, w(1, :)', u1_eksak, err_w1]
disp("Tabel aproksimasi w2,i, solusi eksak u2(t), dan error:");
[t, w(2, :)', u2_eksak, err_w2]
disp("Tabel aproksimasi w3,i, solusi eksak u3(t), dan error:");
[t, w(3, :)', u3_eksak, err_w3]
disp("Error total (norm L1) untuk w1,i:");
disp(err_w1_total);
disp("Error total (norm L1) untuk w2,i:");
disp(err_w2_total);
disp("Error total (norm L1) untuk w3,i:");
disp(err_w3_total);
format;
figure;
hold on;
fplot(sln1, [a, b], 'r');
scatter(t, w(1, :), 'r'); % ambil baris pertama yaitu solusi u1
title("Solusi u1(t) atau y(t)");
legend("Solusi eksak", "w1,i (aproksimasi)");
legend('location', 'northwest');
figure;
hold on;
fplot(sln2, [a, b], 'g');
scatter(t, w(2, :), 'g'); % ambil baris kedua yaitu solusi u2
title("Solusi u2(t) atau y'(t)");
legend("Solusi eksak", "w2,i (aproksimasi)");
legend('location', 'northwest');
figure;
hold on;
fplot(sln3, [a, b], 'b');
scatter(t, w(3, :), 'b'); % ambil baris ketiga yaitu solusi u3
title("Solusi u3(t) atau y''(t)");
legend("Solusi eksak", "w3,i (aproksimasi)");
legend('location', 'northwest');Tabel aproksimasi w1,i, solusi eksak u1(t), dan error:
ans =
1.000000000000000 0 0 0
1.100000000000000 0.116547765077132 0.116547953377741 0.000000188300609
1.200000000000000 0.272737593417178 0.272737913137213 0.000000319720036
1.300000000000000 0.479101055922200 0.479101624357037 0.000000568434836
1.400000000000000 0.746988331768006 0.746998073629463 0.000009741861457
1.500000000000000 1.088479331032411 1.088492594095847 0.000013263063436
1.600000000000001 1.516250804091531 1.516264730431065 0.000013926339534
1.700000000000001 2.043523756922286 2.043536416215900 0.000012659293614
1.800000000000001 2.684004508018369 2.684014851438298 0.000010343419929
1.900000000000001 3.451838703918476 3.451846252199066 0.000007548280589
2.000000000000001 4.361573101909957 4.361577799834785 0.000004697924828
Tabel aproksimasi w2,i, solusi eksak u2(t), dan error:
ans =
1.000000000000000 1.000000000000000 1.000000000000000 0
1.100000000000000 1.346897244698541 1.346898796867440 0.000001552168898
1.200000000000000 1.794476400848503 1.794479954480695 0.000003553632192
1.300000000000000 2.351739790653634 2.351745763551004 0.000005972897370
1.400000000000000 3.026328879302920 3.026307271933378 0.000021607369542
1.500000000000000 3.824765611199535 3.824727552609112 0.000038058590423
1.600000000000001 4.752808495899515 4.752761161714929 0.000047334184586
1.700000000000001 5.815576770936465 5.815525533513762 0.000051237422703
1.800000000000001 7.017677812981450 7.017626495142349 0.000051317839101
1.900000000000001 8.363300595016490 8.363252082824820 0.000048512191670
2.000000000000001 9.856287435428921 9.856243969447302 0.000043465981619
Tabel aproksimasi w3,i, solusi eksak u3(t), dan error:
ans =
Columns 1 through 3:
1.000000000000000e+00 3.000000000000000e+00 3.000000000000000e+00
1.100000000000000e+00 3.956010469157951e+00 3.956018195368995e+00
1.200000000000000e+00 5.010512494112985e+00 5.010526645695958e+00
1.300000000000000e+00 6.147399365577646e+00 6.147418750933507e+00
1.400000000000000e+00 7.354687175512593e+00 7.354710775454516e+00
1.500000000000000e+00 8.623223151179934e+00 8.623257706687671e+00
1.600000000000001e+00 9.945876374658745e+00 9.945922939388453e+00
1.700000000000001e+00 1.131696670232371e+01 1.131702545393904e+01
1.800000000000001e+00 1.273189177401384e+01 1.273196207929798e+01
1.900000000000001e+00 1.418686238954817e+01 1.418694334605300e+01
2.000000000000001e+00 1.567871426475001e+01 1.567880489040572e+01
Column 4:
0
7.726211044278841e-06
1.415158297302099e-05
1.938535586099022e-05
2.359994192246972e-05
3.455550773701077e-05
4.656472970765435e-05
5.875161532742368e-05
7.030528413842774e-05
8.095650483497252e-05
9.062565571049674e-05
Error total (norm L1) untuk w1,i:
7.325663886766087e-05
Error total (norm L1) untuk w2,i:
3.126122781038632e-04
Error total (norm L1) untuk w3,i:
4.466223892567456e-04