function [x, t, w] = parabolik_forward_fd(alph2, f, lb, rb, xb, xu, tb, tu, h, k)
x = xb : h : xu;
t = tb : k : tu;
m_plus_1 = length(x);
N_plus_1 = length(t);
w = zeros(m_plus_1, N_plus_1);
lambd = (alph2 * k) / h^2;
% memasang nilai awal
for i = 1 : m_plus_1
w(i, 1) = f(x(i));
endfor
% memasang syarat batas
for j = 2 : N_plus_1
w(1, j) = lb(t(j));
w(m_plus_1, j) = rb(t(j));
endfor
% menggunakan perumusan finite difference untuk mengisi sisanya
for j = 1 : (N_plus_1 - 1)
for i = 2 : (m_plus_1 - 1)
w(i, j+1) = (1 - 2 * lambd) * w(i, j) + lambd * (w(i+1, j) + w(i-1, j));
endfor
endfor
endfunctionModul 8 Persamaan Diferensial Numerik: PDP Parabolik (persamaan panas/difusi)
Kembali ke Persamaan Diferensial Numerik
Bentuk umum PDP parabolik (lebih tepatnya persamaan panas atau persamaan difusi) bisa ditulis sebagai berikut:
\[\frac{\partial u}{\partial t} (x,t) = \alpha^2 \frac{\partial^2 u}{\partial x^2}(x,t), \quad 0 < x < l, \quad 0 < t < T,\]
dengan syarat batas serta nilai awal
\[u(0,t) = u(l,t) = 0, \quad 0 < t \le T, \quad \text{dan} \quad u(x,0) = f(x), \quad 0 \le x \le l\]
Step size dalam variabel \(x\) bisa ditulis \(h = \Delta x = l/m\) untuk suatu bilangan bulat positif \(m\).
Step size dalam variabel \(t\) bisa ditulis \(k = \Delta t = T/N\) untuk suatu bilangan bulat positif \(N\).
Untuk kebutuhan praktikum, kita dapat menuliskan bentuk umum persamaan panas sebagai berikut:
\[\frac{\partial u}{\partial t} (x,t) = \alpha^2 \frac{\partial^2 u}{\partial x^2}(x,t), \quad \text{xb} < x < \text{xu}, \quad \text{tb} < t < \text{tu},\]
\[u(x,0) = f(x), \quad \text{xb} \le x \le \text{xu}\]
\[u(0,t) = \text{lb}(t) = 0, \quad \text{tb} < t \le \text{tu}\]
\[u(l,t) = \text{rb}(t) = 0, \quad \text{tb} < t \le \text{tu}\]
Metode Forward Difference / Metode Eksplisit untuk PDP Parabolik
Ide utama
Metode forward difference didasari oleh perumusan finite difference berikut,
\[\left(1 - 2 \lambda\right)w_{i,j} - w_{i,j+1} + \lambda \left(w_{i+1,j} + w_{i-1,j}\right) = 0\]
atau bisa ditulis
\[w_{i,j+1} = \left(1 - 2 \lambda\right)w_{i,j} + \lambda \left(w_{i+1,j} + w_{i-1,j}\right)\]
yang kemudian diubah ke dalam bentuk matriks.
Dalam bentuk matriks, langkah-langkah metode forward difference bisa ditulis sebagai berikut.
- Misalkan
\[\lambda = \alpha^2 \left(\frac{k}{h^2}\right)\]
- Susun matriks tridiagonal \(A\) berukuran \((m-1) \times (m-1)\) sebagai berikut:
\[A = \begin{bmatrix} (1-2\lambda) & \lambda & 0 & \cdots & \cdots & \cdots & \cdots & 0 \\ \lambda & (1-2\lambda) & \lambda & 0 & \ddots & \ddots & \ddots & \vdots \\ 0 & \lambda & (1-2\lambda) & \lambda & 0 & \ddots & \ddots & \vdots \\ \vdots & \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & \vdots \\ \vdots & \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & \vdots \\ \vdots & \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & \vdots \\ 0 & \cdots & \cdots & \cdots & 0 & \lambda & (1-2\lambda) & \lambda \\ 0 & \cdots & \cdots & \cdots & \cdots & 0 & \lambda & (1-2\lambda) \end{bmatrix}\]
Siapkan matriks grid \(w\) berukuran \((m+1) \times (N+1)\) untuk menyimpan \(w_{i,j}\).
Isi semua dengan nol terlebih dahulu, atau setidaknya, pastikan baris pertama dan baris terakhir terisi nol semua (sesuai syarat batas).
Misalkan kolom ke-\(j\), kecuali baris pertama dan baris terakhir, ditulis \(\textbf{w}^{(j)}\), yaitu
\[\textbf{w}^{(j)} = (w_{2,j}, w_{3,j}, \dots, w_{m,j})\]
Isi kolom pertama \(w\) berdasarkan nilai awal, yaitu
\[w_{i,1} = f(x_i)\]
atau bisa ditulis
\[\textbf{w}^{(1)} = (f(x_2), f(x_3), \dots, f(x_m))\]
Untuk \(j = 2, \dots, N+1\), isi kolom ke-\(j\) dengan perkalian matriks
\[\textbf{w}^{(j)} = A\textbf{w}^{(j-1)}\]
Function file (dengan perumusan finite difference)
Function file (dengan perumusan matriks)
function [x, t, w] = parabolik_forward_matriks(alph2, f, lb, rb, xb, xu, tb, tu, h, k)
x = xb : h : xu;
t = tb : k : tu;
m_plus_1 = length(x);
N_plus_1 = length(t);
w = zeros(m_plus_1, N_plus_1);
lambd = (alph2 * k) / h^2;
% memasang nilai awal
for i = 1 : m_plus_1
w(i, 1) = f(x(i));
endfor
% memasang syarat batas
for j = 2 : N_plus_1
w(1, j) = lb(t(j));
w(m_plus_1, j) = rb(t(j));
endfor
% menyusun matriks A
A = zeros(m_plus_1 - 2, m_plus_1 - 2); % isi dulu dengan nol semua
for i = 1 : (m_plus_1 - 2) % untuk tiap baris ke-i
% isi sebelah kiri/bawah diagonal (kecuali baris pertama)
if (i > 1)
A(i, i-1) = lambd;
endif
% isi diagonal
A(i, i) = 1 - 2 * lambd;
% isi sebelah kanan/atas diagonal (kecuali baris terakhir)
if (i < m_plus_1 - 2)
A(i, i+1) = lambd;
endif
endfor
% perkalian matriks untuk mengisi semua nilai lainnya
for j = 2 : N_plus_1 % untuk tiap waktu ke-j selain nilai awal
w(2 : m_plus_1 - 1, j) = A * w(2 : m_plus_1 - 1, j-1);
endfor
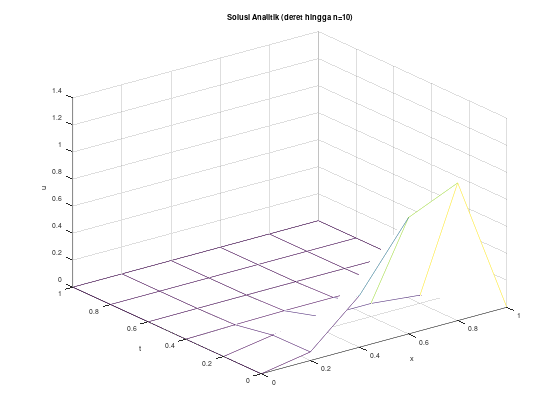
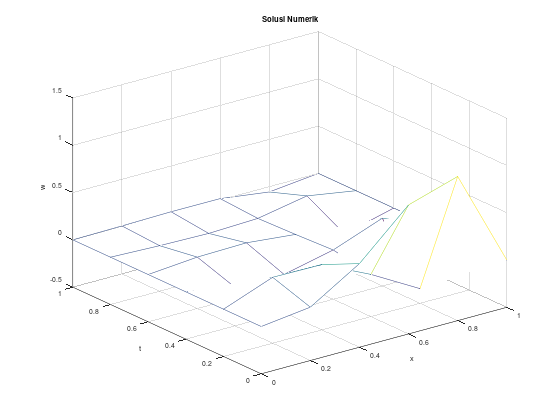
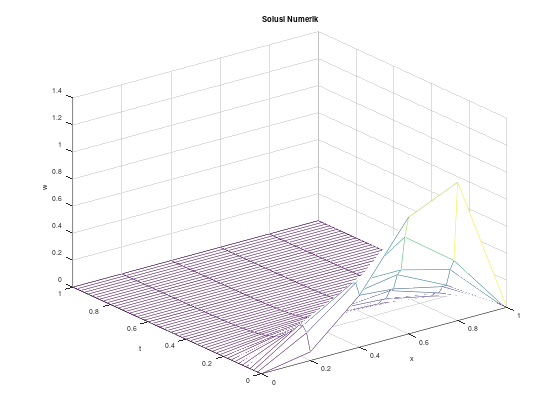
endfunctionContoh (stabil) dengan \(h = 0.2\), \(k = 0.02\), solusi eksak berupa deret
Akan kita uji menggunakan persamaan panas:
\[\begin{align*} u_t - u_{xx} &= 0, \quad 0 < x < 1, \quad t > 0 \\ u(0,t) &= u(1,t) = 0, \quad t \le 0 \\ u(x,0) &= 10x^3(1-x), \quad 0 \le x \le 1 \\ \end{align*}\]
Solusi eksak dari PDP tersebut adalah:
\[\begin{align*} u(x,t) &= \sum_{n=1}^{\infty} c_n e^{-n^2 \pi^2 t} \sin \left( n\pi x\right) \\ c_n &= 20 \int_0^1 x^3 (1-x) \sin \left( n\pi x \right) dx, \quad n = 1, 2, \dots \end{align*}\]
Untuk keperluan komputasi, untuk solusi eksak, akan kita ambil 10 suku pertama dari ekspansi deret Fourier dari u(x,t).
Perhatikan bahwa \(\alpha^2 = 1\) sehingga
\[\lambda = \frac{\alpha^2 k}{h^2} = \frac{(1)(0.02)}{(0.2)^2} = \frac{0.02}{0.04} = \frac{1}{2} \le \frac{1}{2}\]
Oleh karena itu, metode forward difference dijamin stabil untuk pemilihan step size ini.
Menggunakan pendekatan finite difference:
alph2 = 1;
f = @(x) 10 * x .^ 3 .* (1 - x);
lb = @(t) 0;
rb = @(t) 0;
xb = 0;
xu = 1;
tb = 0;
tu = 1;
h = 0.2;
k = 0.02;
[x, t, w] = parabolik_forward_fd(alph2, f, lb, rb, xb, xu, tb, tu, h, k);
u = zeros(length(x), length(t));
for i = 1 : length(x)
for j = 1 : length(t)
u(i, j) = 0;
for n = 1 : 10
F = @(x) x .^ 3 .* (1 - x) .* sin(n * pi .* x);
cn = 20 * integral(F, 0, 1);
u(i, j) += cn * exp(-n^2 * pi^2 .* t(j)) .* sin(n * pi .* x(i));
endfor
endfor
endfor
figure 1;
mesh(x, t, w');
title("Solusi Numerik");
xlabel("x");
ylabel("t");
zlabel("w");
figure 2;
mesh(x, t, u');
title("Solusi Analitik (deret hingga n=10)");
xlabel("x");
ylabel("t");
zlabel("u");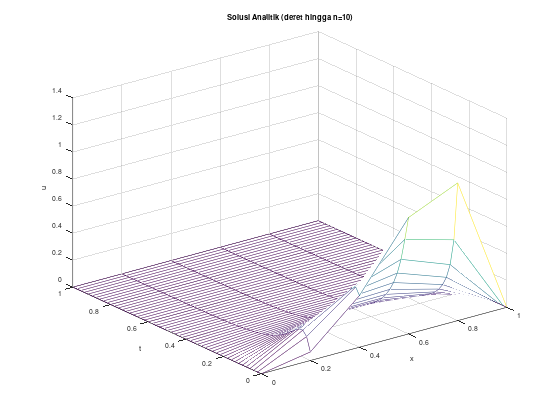
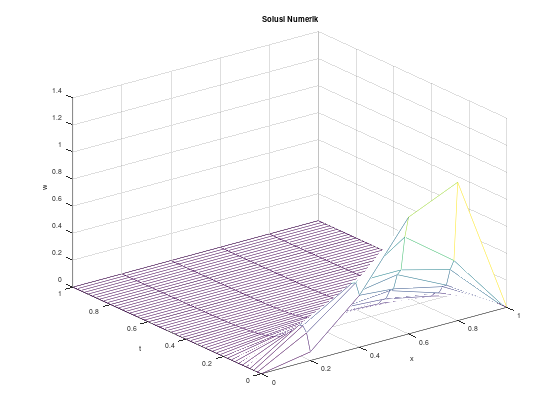
Alternatifnya, menggunakan bentuk matriks:
alph2 = 1;
f = @(x) 10 * x .^ 3 .* (1 - x);
lb = @(t) 0;
rb = @(t) 0;
xb = 0;
xu = 1;
tb = 0;
tu = 1;
h = 0.2;
k = 0.02;
[x, t, w] = parabolik_forward_matriks(alph2, f, lb, rb, xb, xu, tb, tu, h, k);
u = zeros(length(x), length(t));
for i = 1 : length(x)
for j = 1 : length(t)
u(i, j) = 0;
for n = 1 : 10
F = @(x) x .^ 3 .* (1 - x) .* sin(n * pi .* x);
cn = 20 * integral(F, 0, 1);
u(i, j) += cn * exp(-n^2 * pi^2 .* t(j)) .* sin(n * pi .* x(i));
endfor
endfor
endfor
figure 1;
mesh(x, t, w');
title("Solusi Numerik");
xlabel("x");
ylabel("t");
zlabel("w");
figure 2;
mesh(x, t, u');
title("Solusi Analitik (deret hingga n=10)");
xlabel("x");
ylabel("t");
zlabel("u");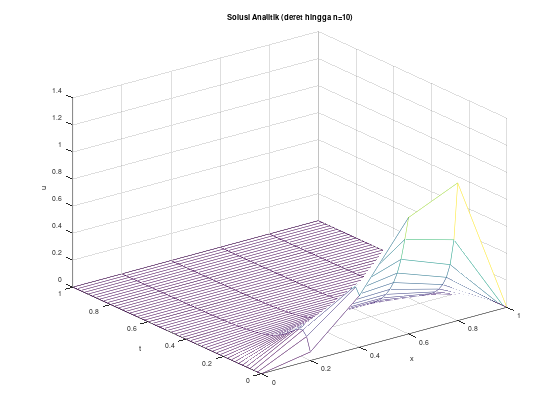
Baik menggunakan pendekatan finite difference maupun bentuk matriks, Anda juga bisa menampilkan animasi persebaran suhu yang terus menurun, dengan menambahkan kode berikut di akhir script file:
figure(3);
for j = 1:length(t)
plot(x, u(:, j), 'k', 'linewidth', 1.5);
ylim([0, 1.5]);
title("Animasi solusi aproksimasi u(x, t) seiring berjalannya t");
drawnow;
pause(0.1);
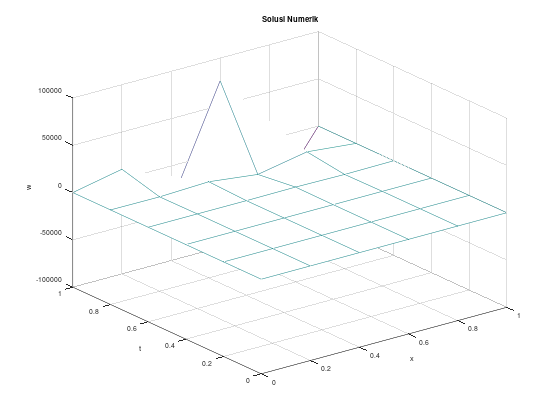
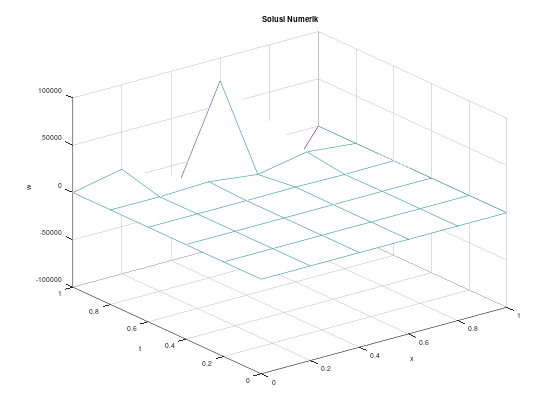
endforContoh (tidak stabil) dengan \(h = k = 0.2\), solusi eksak berupa deret
Menggunakan soal yang sama,
\[\begin{align*} u_t - u_{xx} &= 0, \quad 0 < x < 1, \quad t > 0 \\ u(0,t) &= u(1,t) = 0, \quad t \le 0 \\ u(x,0) &= 10x^3(1-x), \quad 0 \le x \le 1 \\ \end{align*}\]
Solusi eksak dari PDP tersebut adalah:
\[\begin{align*} u(x,t) &= \sum_{n=1}^{\infty} c_n e^{-n^2 \pi^2 t} \sin \left( n\pi x\right) \\ c_n &= 20 \int_0^1 x^3 (1-x) \sin \left( n\pi x \right) dx, \quad n = 1, 2, \dots \end{align*}\]
Perhatikan bahwa \(\alpha^2 = 1\) sehingga
\[\lambda = \frac{\alpha^2 k}{h^2} = \frac{(1)(0.2)}{(0.2)^2} = \frac{0.2}{0.04} = 5 > \frac{1}{2}\]
Oleh karena itu, metode forward difference tidak dijamin stabil untuk pemilihan step size ini. Mari kita lihat.
Untuk pendekatan finite difference:
alph2 = 1;
f = @(x) 10 * x .^ 3 .* (1 - x);
lb = @(t) 0;
rb = @(t) 0;
xb = 0;
xu = 1;
tb = 0;
tu = 1;
h = 0.2;
k = 0.2;
[x, t, w] = parabolik_forward_fd(alph2, f, lb, rb, xb, xu, tb, tu, h, k);
u = zeros(length(x), length(t));
for i = 1 : length(x)
for j = 1 : length(t)
u(i, j) = 0;
for n = 1 : 10
F = @(x) x .^ 3 .* (1 - x) .* sin(n * pi .* x);
cn = 20 * integral(F, 0, 1);
u(i, j) += cn * exp(-n^2 * pi^2 .* t(j)) .* sin(n * pi .* x(i));
endfor
endfor
endfor
figure 1;
mesh(x, t, w');
title("Solusi Numerik");
xlabel("x");
ylabel("t");
zlabel("w");
figure 2;
mesh(x, t, u');
title("Solusi Analitik (deret hingga n=10)");
xlabel("x");
ylabel("t");
zlabel("u");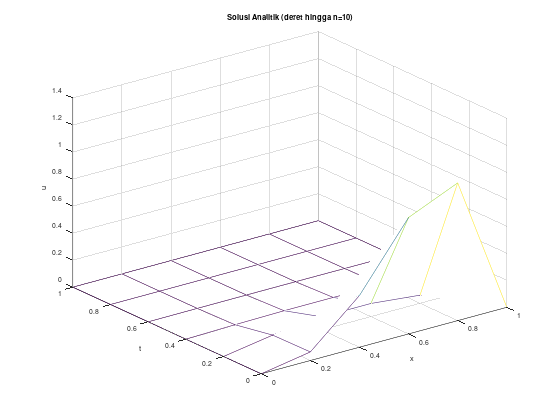
Untuk pendekatan bentuk matriks:
alph2 = 1;
f = @(x) 10 * x .^ 3 .* (1 - x);
lb = @(t) 0;
rb = @(t) 0;
xb = 0;
xu = 1;
tb = 0;
tu = 1;
h = 0.2;
k = 0.2;
[x, t, w] = parabolik_forward_matriks(alph2, f, lb, rb, xb, xu, tb, tu, h, k);
u = zeros(length(x), length(t));
for i = 1 : length(x)
for j = 1 : length(t)
u(i, j) = 0;
for n = 1 : 10
F = @(x) x .^ 3 .* (1 - x) .* sin(n * pi .* x);
cn = 20 * integral(F, 0, 1);
u(i, j) += cn * exp(-n^2 * pi^2 .* t(j)) .* sin(n * pi .* x(i));
endfor
endfor
endfor
figure 1;
mesh(x, t, w');
title("Solusi Numerik");
xlabel("x");
ylabel("t");
zlabel("w");
figure 2;
mesh(x, t, u');
title("Solusi Analitik (deret hingga n=10)");
xlabel("x");
ylabel("t");
zlabel("u");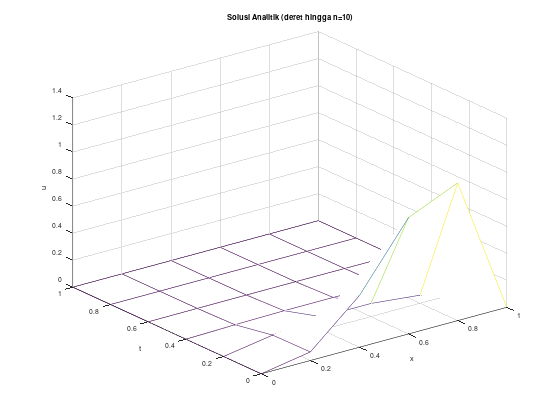
Contoh lain, solusi eksak berupa fungsi
Akan kita uji dengan persamaan difusi:
\[\begin{align*} u_t - u_{xx} &= 0, \quad 0 < x < 1, \quad t > 0, \\ u(0,t) &= u(1,t) = 0, \quad t > 0, \\ u(x,0) &= \sin \left(\pi x\right), \quad 0 \le x \le 1 \end{align*}\]
dengan solusi eksak:
\[u(x,t) = e^{-\pi^2 t} \sin \left(\pi x\right)\]
Gunakan \(h = 0.2\), \(k = 0.01\), dan \(T = 0.5\).
Apabila digunakan pendekatan finite difference:
alph2 = 1;
f = @(x) sin(pi * x);
lb = @(t) 0;
rb = @(t) 0;
xb = 0;
xu = 1;
tb = 0;
tu = 0.5; % T
h = 0.2;
k = 0.01;
[x_arr, t_arr, w] = parabolik_forward_fd(alph2, f, lb, rb, xb, xu, tb, tu, h, k);
% solusi eksak
u = zeros(length(x_arr), length(t_arr));
sln = @(x, t) exp(-pi^2.*t) * sin(pi.*x);
for i = 1 : length(x_arr)
for j = 1 : length(t_arr)
u(i, j) = sln(x_arr(i), t_arr(j));
endfor
endfor
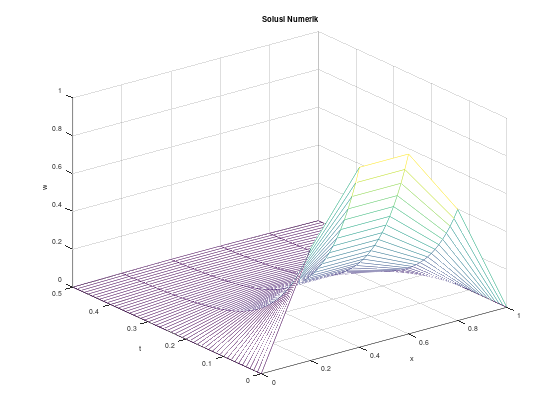
figure 1;
mesh(x_arr, t_arr, w');
title("Solusi Numerik");
xlabel("x");
ylabel("t");
zlabel("w");
figure 2;
mesh(x_arr, t_arr, u');
title("Solusi Analitik");
xlabel("x");
ylabel("t");
zlabel("u");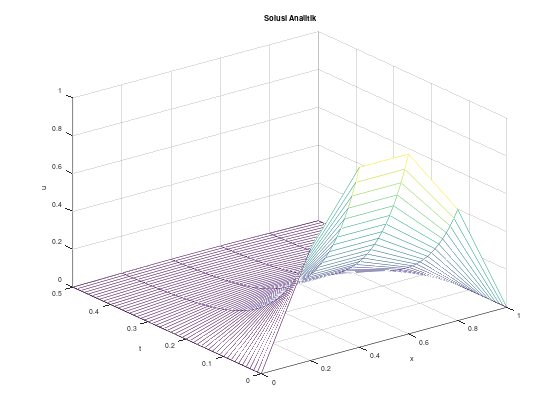
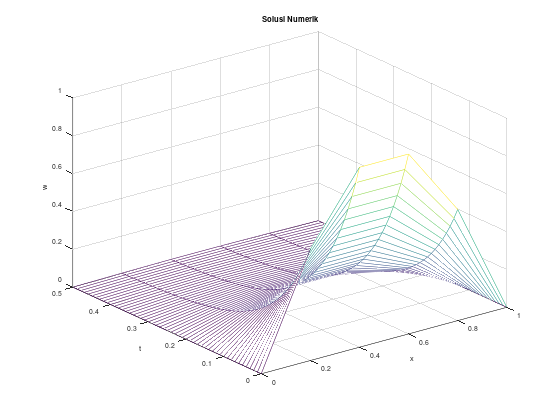
Apabila digunakan pendekatan matriks:
alph2 = 1;
f = @(x) sin(pi * x);
lb = @(t) 0;
rb = @(t) 0;
xb = 0;
xu = 1;
tb = 0;
tu = 0.5; % T
h = 0.2;
k = 0.01;
[x_arr, t_arr, w] = parabolik_forward_matriks(alph2, f, lb, rb, xb, xu, tb, tu, h, k);
% solusi eksak
u = zeros(length(x_arr), length(t_arr));
sln = @(x, t) exp(-pi^2.*t) * sin(pi.*x);
for i = 1 : length(x_arr)
for j = 1 : length(t_arr)
u(i, j) = sln(x_arr(i), t_arr(j));
endfor
endfor
figure 1;
mesh(x_arr, t_arr, w');
title("Solusi Numerik");
xlabel("x");
ylabel("t");
zlabel("w");
figure 2;
mesh(x_arr, t_arr, u');
title("Solusi Analitik");
xlabel("x");
ylabel("t");
zlabel("u");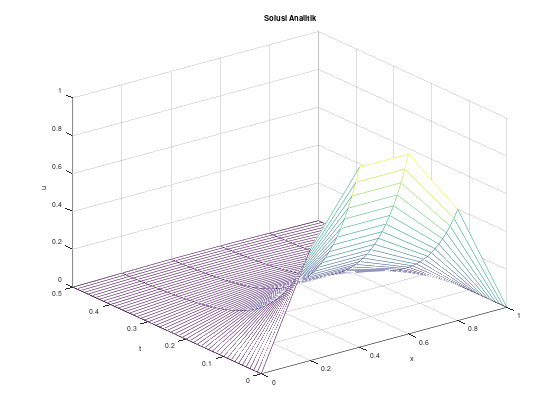
Metode Backward Difference untuk PDP Parabolik
Ide utama
Function file (dengan faktorisasi Crout sesuai pseudocode)
function [x, t, w] = parabolik_backward_crout(d, f, lb, rb, xb, xu, tb, tu, dx, dt)
x = xb:dx:xu;
t = tb:dt:tu;
nx = length(x);
nt = length(t);
% Nilai lambda
lambd = (d * dt) / (dx^2);
% Nilai awal dan syarat batas
for i = 1:nx
w(i, 1) = f(x(i));
endfor
for j = 2:nt
w(1, j) = lb(t(j));
w(nx, j) = rb(t(j));
endfor
% Penyelesaian SPL dengan faktorisasi Crout
l(2) = 1 + 2*lambd;
u(2) = -lambd / l(2);
for i = 3:nx-2
l(i) = 1 + 2*lambd + lambd*u(i-1);
u(i) = -lambd / l(i);
endfor
l(nx-1) = 1 + 2*lambd + lambd*u(nx-2);
for j = 2:nt
z(2) = w(2, j-1) / l(2);
for i = 3:nx-1
z(i) = (w(i, j-1) + lambd*z(i-1)) / l(i);
endfor
w(nx-1, j) = z(nx-1);
for i = nx-2:-1:2
w(i, j) = z(i) - u(i)*w(i+1, j);
endfor
endfor
endfunctionFunction file (dengan solusi SPL secara langsung)
function [x, t, u] = parabolik_backward_langsung(alph2, f, lb, rb, xb, xu, tb, tu, h, k)
x = xb : h : xu;
t = tb : k : tu;
m_plus_1 = length(x);
N_plus_1 = length(t);
u = zeros(m_plus_1, N_plus_1);
lambd = (alph2 * k) / h^2;
% memasang nilai awal
for i = 1 : m_plus_1
u(i, 1) = f(x(i));
endfor
% memasang syarat batas
for j = 2 : N_plus_1
u(1, j) = lb(t(j));
u(m_plus_1, j) = rb(t(j));
endfor
% menyusun matriks A
A = zeros(m_plus_1 - 2, m_plus_1 - 2);
for i = 1 : (m_plus_1 - 2)
% isi sebelah kiri/atas diagonal
if (i > 1)
A(i, i-1) = -lambd;
endif
% isi diagonal
A(i, i) = 1 + 2 * lambd;
% isi sebelah kanan/bawah diagonal
if (i < m_plus_1 - 2)
A(i, i+1) = -lambd;
endif
endfor
% mengisi semua nilai lainnya dengan penyelesaian SPL
for j = 2 : N_plus_1
u(2 : m_plus_1 - 1, j) = A \ u(2 : m_plus_1 - 1, j-1);
endfor
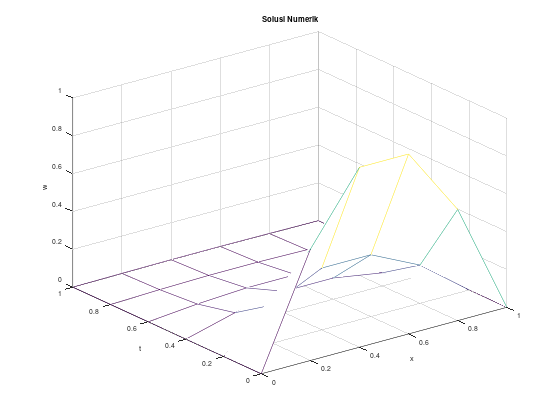
endfunctionContoh 1, solusi eksak berupa fungsi
Akan kita uji dengan persamaan difusi:
\[\begin{align*} u_t - u_{xx} &= 0, \quad 0 < x < 1, \quad t > 0, \\ u(0,t) &= u(1,t) = 0, \quad t > 0, \\ u(x,0) &= \sin \left(\pi x\right), \quad 0 \le x \le 1 \end{align*}\]
dengan solusi eksak:
\[u(x,t) = e^{-\pi^2 t} \sin \left(\pi x\right)\]
Kita batasi \(t\) menjadi \(0 \le t \le 1\) dan gunakan \(\Delta x = 0.2\) dan \(\Delta t = 0.2\), di mana kondisinya tidak stabil untuk metode eksplisit.
Menggunakan function file dari pseudocode:
d = 1;
f = @(x) sin(pi*x);
lb = rb = @(t) 0;
xb = 0;
xu = 1;
tb = 0;
tu = 1;
dx = 0.2;
dt = 0.2;
[x, t, w] = parabolik_backward_crout(d, f, lb, rb, xb, xu, tb, tu, dx, dt);
u = @(x, t) exp(-pi^2.*t) * sin(pi.*x);
for i = 1:length(x)
for j = 1:length(t)
ufig(i, j) = u(x(i), t(j));
endfor
endfor
figure(1);
mesh(x, t, ufig');
xlabel("x");
ylabel("t");
zlabel("u");
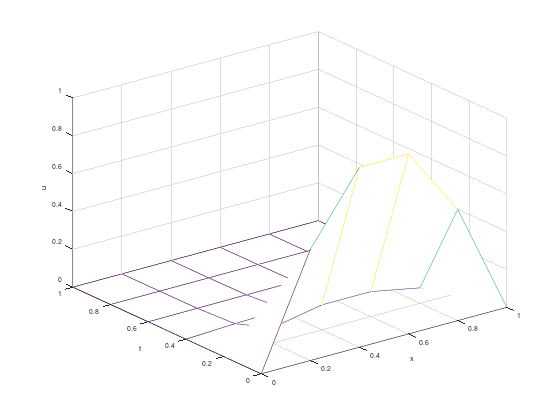
figure(2);
mesh(x, t, w');
xlabel("x");
ylabel("t");
zlabel("u");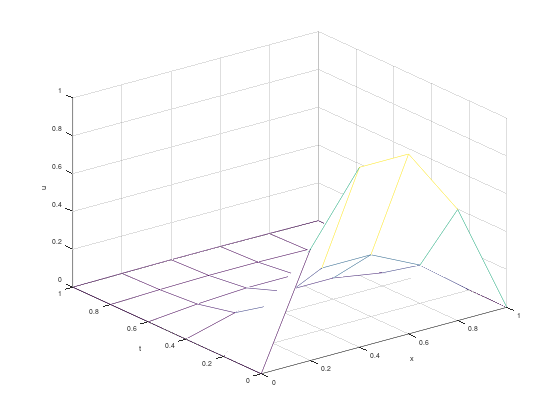
Menggunakan function file dengan solusi SPL secara langsung:
d = 1;
f = @(x) sin(pi*x);
lb = rb = @(t) 0;
xb = 0;
xu = 1;
tb = 0;
tu = 1;
h = 0.2;
k = 0.2;
[x_arr, t_arr, w] = parabolik_backward_langsung(alph2, f, lb, rb, xb, xu, tb, tu, h, k);
% solusi eksak
u = zeros(length(x_arr), length(t_arr));
sln = @(x, t) exp(-pi^2.*t) * sin(pi.*x);
for i = 1 : length(x_arr)
for j = 1 : length(t_arr)
u(i, j) = sln(x_arr(i), t_arr(j));
endfor
endfor
figure 1;
mesh(x_arr, t_arr, w');
title("Solusi Numerik");
xlabel("x");
ylabel("t");
zlabel("w");
figure 2;
mesh(x_arr, t_arr, u');
title("Solusi Analitik");
xlabel("x");
ylabel("t");
zlabel("u");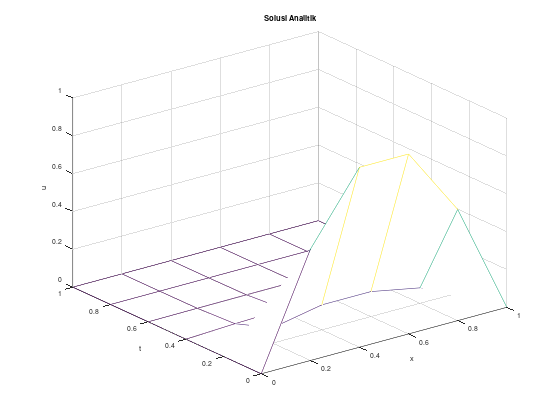
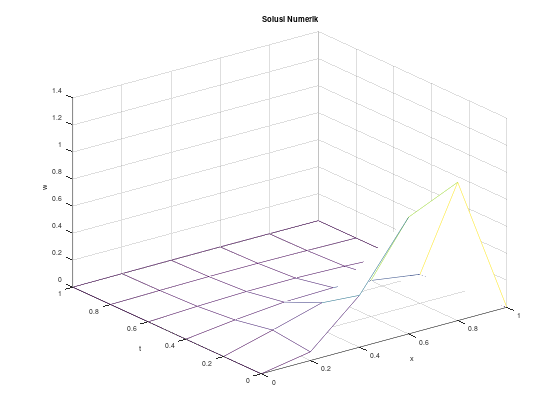
Contoh 2, solusi eksak berupa deret
Akan kita uji menggunakan persamaan panas:
\[\begin{align*} u_t - u_{xx} &= 0, \quad 0 < x < 1, \quad t > 0 \\ u(0,t) &= u(1,t) = 0, \quad t \le 0 \\ u(x,0) &= 10x^3(1-x), \quad 0 \le x \le 1 \\ \end{align*}\]
Solusi eksak dari PDP tersebut adalah:
\[\begin{align*} u(x,t) &= \sum_{n=1}^{\infty} c_n e^{-n^2 \pi^2 t} \sin \left( n\pi x\right) \\ c_n &= 20 \int_0^1 x^3 (1-x) \sin \left( n\pi x \right) dx, \quad n = 1, 2, \dots \end{align*}\]
Untuk keperluan komputasi, untuk solusi eksak, akan kita ambil 10 suku pertama dari ekspansi deret Fourier dari u(x,t).
alph2 = 1;
f = @(x) 10 * x .^ 3 .* (1 - x);
lb = @(t) 0;
rb = @(t) 0;
xb = 0;
xu = 1;
tb = 0;
tu = 1;
h = 0.2;
k = 0.2;
[x, t, w] = parabolik_backward_langsung(alph2, f, lb, rb, xb, xu, tb, tu, h, k);
u = zeros(length(x), length(t));
for i = 1 : length(x)
for j = 1 : length(t)
u(i, j) = 0;
for n = 1 : 10
F = @(x) x .^ 3 .* (1 - x) .* sin(n * pi .* x);
cn = 20 * integral(F, 0, 1);
u(i, j) += cn * exp(-n^2 * pi^2 .* t(j)) .* sin(n * pi .* x(i));
endfor
endfor
endfor
figure 1;
mesh(x, t, w');
title("Solusi Numerik");
xlabel("x");
ylabel("t");
zlabel("w");
figure 2;
mesh(x, t, u');
title("Solusi Analitik (deret hingga n=10)");
xlabel("x");
ylabel("t");
zlabel("u");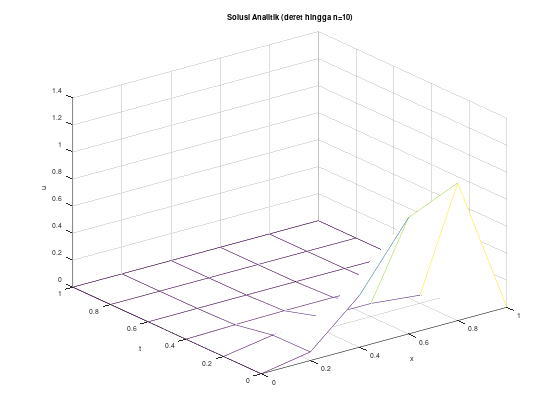
Metode Crack-Nicolson untuk PDP Parabolik
Ide utama
Function file (dengan faktorisasi Crout sesuai pseudocode)
function [x, t, w] = crank_nicolson_crout(d, f, lb, rb, xb, xu, tb, tu, dx, dt)
x = xb:dx:xu;
t = tb:dt:tu;
nx = length(x);
nt = length(t);
% Nilai lambda
lambd = (d * dt) / (dx^2);
% Nilai awal dan syarat batas
for i = 1:nx
w(i, 1) = f(x(i));
endfor
for j = 2:nt
w(1, j) = lb(t(j));
w(nx, j) = rb(t(j));
endfor
% Penyelesaian SPL menggunakan faktorisasi Crout
l(2) = 1 + lambd;
u(2) = -lambd / (2*l(2));
for i = 3:nx-2
l(i) = 1 + lambd + (lambd*u(i-1))/2;
u(i) = -lambd / (2*l(i));
endfor
l(nx-1) = 1 + lambd + (lambd*u(nx-2))/2;
for j = 2:nt
z(2) = ((1-lambd)*w(2, j-1) + (lambd/2)*w(3, j-1)) / l(2);
for i = 3:nx-1
z(i) = ((1-lambd)*w(i, j-1) + (lambd/2)*(w(i+1, j-1) + w(i-1, j-1) + z(i-
1))) / l(i);
endfor
w(nx-1, j) = z(nx-1);
for i = nx-2:-1:2
w(i, j) = z(i) - u(i)*w(i+1, j);
endfor
endfor
endfunctionFunction file (dengan solusi SPL secara langsung)
function [x, t, w] = crank_nicolson_langsung(alph2, f, lb, rb, xb, xu, tb, tu, h, k)
x = xb : h : xu;
t = tb : k : tu;
m_plus_1 = length(x);
N_plus_1 = length(t);
w = zeros(m_plus_1, N_plus_1);
lambda = (alph2 * k) / h^2;
% memasang nilai awal
for i = 1 : m_plus_1
w(i, 1) = f(x(i));
endfor
% memasang syarat batas
for j = 2 : N_plus_1
w(1, j) = lb(t(j));
w(m_plus_1, j) = rb(t(j));
endfor
% menyusun matriks A
A = zeros(m_plus_1 - 2, m_plus_1 - 2);
for i = 1 : (m_plus_1 - 2)
% isi sebelah kiri/atas diagonal
if (i > 1)
A(i, i-1) = -lambda/2;
endif
% isi diagonal
A(i, i) = 1 + lambda;
% isi sebelah kanan/bawah diagonal
if (i < m_plus_1 - 2)
A(i, i+1) = -lambda/2;
endif
endfor
% menyusun matriks B
B = zeros(m_plus_1 - 2, m_plus_1 - 2);
for i = 1 : (m_plus_1 - 2)
% isi sebelah kiri/atas diagonal
if (i > 1)
B(i, i-1) = lambda/2;
endif
% isi diagonal
B(i, i) = 1 - lambda;
% isi sebelah kanan/bawah diagonal
if (i < m_plus_1 - 2)
B(i, i+1) = lambda/2;
endif
endfor
% penyelesaian Aw^(j) = Bw^(j-1):
% misalkan z = Bw^(j-1), lalu selesaikan Aw^(j) = z
for j = 2 : N_plus_1
z = B * w(2 : m_plus_1 - 1, j-1);
w(2 : m_plus_1 - 1, j) = A \ z;
endfor
endfunctionContoh 1, solusi eksak berupa fungsi
Sama seperti untuk backward difference, akan kita uji dengan persamaan difusi:
\[\begin{align*} u_t - u_{xx} &= 0, \quad 0 < x < 1, \quad t > 0, \\ u(0,t) &= u(1,t) = 0, \quad t > 0, \\ u(x,0) &= \sin \left(\pi x\right), \quad 0 \le x \le 1 \end{align*}\]
dengan solusi eksak:
\[u(x,t) = e^{-\pi^2 t} \sin \left(\pi x\right)\]
Kita batasi \(t\) menjadi \(0 \le t \le 1\) dan gunakan \(\Delta x = 0.2\) dan \(\Delta k = 0.2\), di mana kondisinya tidak stabil untuk metode eksplisit.
Menggunakan function file dari pseudocode:
d = 1;
f = @(x) sin(pi*x);
lb = rb = @(t) 0;
xb = 0;
xu = 1;
tb = 0;
tu = 1;
dx = 0.2;
dt = 0.2;
[x, t, w] = crank_nicolson_crout(d, f, lb, rb, xb, xu, tb, tu, dx, dt);
u = @(x, t) exp(-pi^2.*t) * sin(pi.*x);
for i = 1:length(x)
for j = 1:length(t)
ufig(i, j) = u(x(i), t(j));
endfor
endfor
figure(1);
mesh(x, t, ufig');
xlabel("x");
ylabel("t");
zlabel("u");
figure(2);
mesh(x, t, w');
xlabel("x");
ylabel("t");
zlabel("u");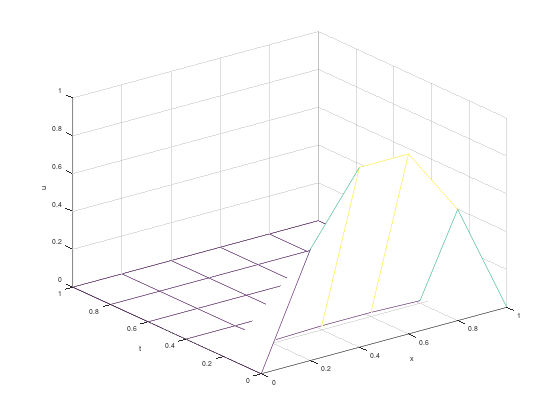
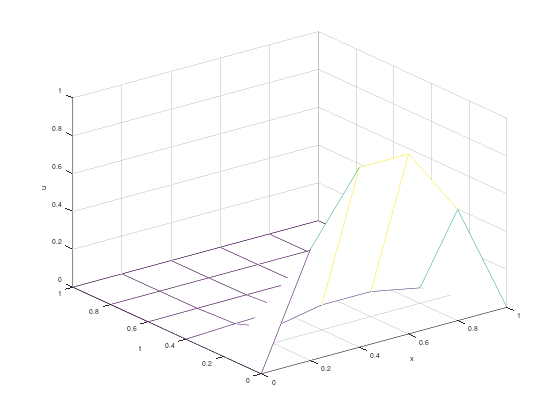
Menggunakan function file dengan penyelesaian SPL secara langsung:
alph2 = 1;
f = @(x) sin(pi*x);
lb = @(t) 0;
rb = @(t) 0;
xb = 0;
xu = 1;
tb = 0;
tu = 1;
h = 0.2;
k = 0.2;
[x, t, w] = crank_nicolson_langsung(alph2, f, lb, rb, xb, xu, tb, tu, h, k);
u = zeros(length(x), length(t));
sln = @(x, t) exp(-pi^2.*t) * sin(pi.*x);
for i = 1:length(x)
for j = 1:length(t)
u(i, j) = sln(x(i), t(j));
endfor
endfor
figure 1;
mesh(x, t, w');
title("Solusi Numerik");
xlabel("x");
ylabel("t");
zlabel("w");
figure 2;
mesh(x, t, u');
title("Solusi Analitik (deret hingga n=10)");
xlabel("x");
ylabel("t");
zlabel("u");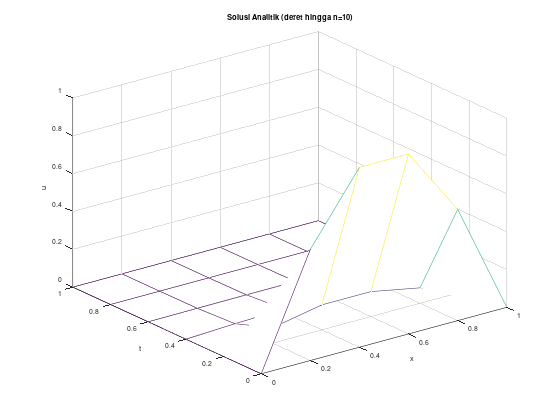
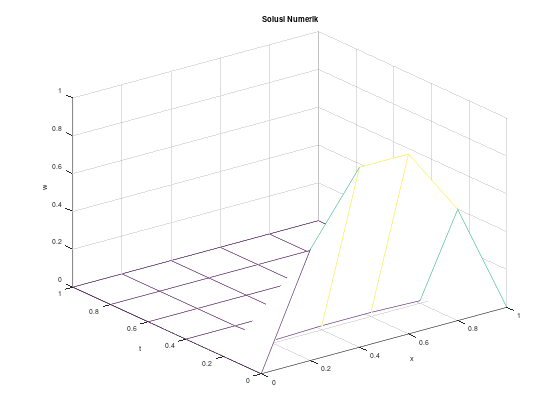
Contoh 2, solusi eksak berupa deret
Akan kita uji menggunakan persamaan panas:
\[\begin{align*} u_t - u_{xx} &= 0, \quad 0 < x < 1, \quad t > 0 \\ u(0,t) &= u(1,t) = 0, \quad t \le 0 \\ u(x,0) &= 10x^3(1-x), \quad 0 \le x \le 1 \\ \end{align*}\]
Solusi eksak dari PDP tersebut adalah:
\[\begin{align*} u(x,t) &= \sum_{n=1}^{\infty} c_n e^{-n^2 \pi^2 t} \sin \left( n\pi x\right) \\ c_n &= 20 \int_0^1 x^3 (1-x) \sin \left( n\pi x \right) dx, \quad n = 1, 2, \dots \end{align*}\]
Menggunakan function file dengan solusi SPL secara langsung:
alph2 = 1;
f = @(x) 10 * x .^ 3 .* (1 - x);
lb = @(t) 0;
rb = @(t) 0;
xb = 0;
xu = 1;
tb = 0;
tu = 1;
h = 0.2;
k = 0.2;
[x, t, w] = crank_nicolson_langsung(alph2, f, lb, rb, xb, xu, tb, tu, h, k);
u = zeros(length(x), length(t));
for i = 1 : length(x)
for j = 1 : length(t)
u(i, j) = 0;
for n = 1 : 10
F = @(x) x .^ 3 .* (1 - x) .* sin(n * pi .* x);
cn = 20 * integral(F, 0, 1);
u(i, j) += cn * exp(-n^2 * pi^2 .* t(j)) .* sin(n * pi .* x(i));
endfor
endfor
endfor
figure 1;
mesh(x, t, w');
title("Solusi Numerik");
xlabel("x");
ylabel("t");
zlabel("w");
figure 2;
mesh(x, t, u');
title("Solusi Analitik (deret hingga n=10)");
xlabel("x");
ylabel("t");
zlabel("u");