Latihan 1 Praktikum Persamaan Diferensial Biasa: Metode Euler

Soal

Diberikan suatu masalah nilai awal (Initial Value Problem):

\[ \begin{align*} y' &= 1 + \cfrac{y}{t} + \left(\cfrac{y}{t}\right)^2\\ & y(1) = 0 \nonumber \end{align*} \]

Diberikan pada interval \(1\leq t\leq 3\) dengan stepsize \(h = 0.2\)

Diketahui bahwa solusi eksak dari model diberikan oleh

\[ \begin{align*} y(t) = t \tan{(\ln t)} \end{align*} \]

Buatlah script file nama_kelas_npm.m (contoh: Pandu Adjie_C_1234567890.m) berisi penggunaan metode Euler untuk mengaproksimasi solusi dari model secara numerik !
Tunjukkan solusi aproksimasi anda dalam bentuk plot dan tentukan 1 dari aproksimasi dibandingkan dengan solusi eksak !

Solusi

Pertama, buat function file euler.m terlebih dahulu pada direktori anda, misalnya seperti pada folder **F:*.

Function file euler.m - nama file harus sama dengan nama fungsi

function [t, w] = euler(f, a, b, N, alpha)
    h = (b - a) / N;
    t = zeros(N + 1, 1);
    w = zeros(N + 1, 1);
    t(1) = a;
    w(1) = alpha;

    for i = 1 : N
        t(i + 1) = t(i) + h;
        m1 = f(t(i), w(i));
        w(i + 1) = w(i) + h * m1;
    endfor
endfunction

Langkah berikutnya anda membuat script file dengan nama file bebas, berisi instruksi untuk menjalankan metode euler berdasarkan nilai awal yang diketahui sebagai berikut.

% full-setup
f = @(t, y) (1 + y/t + (y/t)^2);
a = 1;
b = 3;
N = 10;
alpha= 0;


[t_euler, w_euler] = euler(f, a, b, N, alpha);


sln = @(t) (t).*tan(log(t));
y_eksak = sln(t_euler); 


err_euler = abs(y_eksak - w_euler);

err_euler_total = sum(err_euler);


disp("Tabel aproksimasi w, solusi eksak y, dan error:");
[t_euler, w_euler, y_eksak, err_euler]

disp("Error total (norm L1):");
disp(err_euler_total);


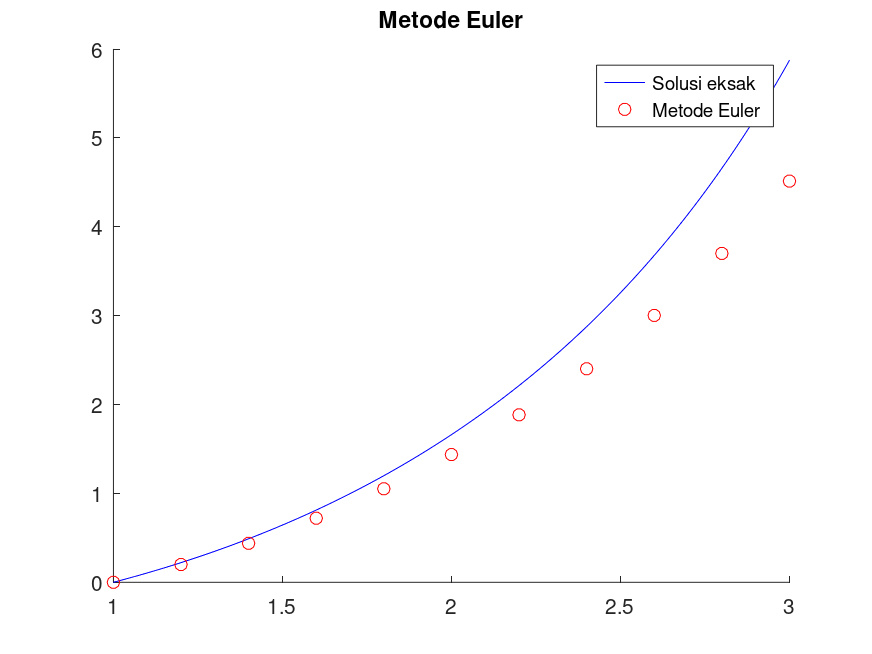
hold on;
fplot(sln, [a, b], 'b');
scatter(t_euler, w_euler, 'r');
legend('Solusi eksak', 'Metode Euler');
title("Metode Euler");

Tabel aproksimasi w, solusi eksak y, dan error:
ans =

   1.0000        0        0        0
   1.2000   0.2000   0.2212   0.0212
   1.4000   0.4389   0.4897   0.0508
   1.6000   0.7212   0.8128   0.0915
   1.8000   1.0520   1.1994   0.1474
   2.0000   1.4373   1.6613   0.2240
   2.2000   1.8843   2.2135   0.3292
   2.4000   2.4023   2.8766   0.4743
   2.6000   3.0028   3.6785   0.6756
   2.8000   3.7006   4.6587   0.9581
   3.0000   4.5143   5.8741   1.3598

Error total (norm L1):
4.3320