Petunjuk Umum:
Kerjakan secara Individu
Kerjakan tugas ini menggunakan bahasa pemrograman Python dengan file format berupa interactive Python notebook (yaitu file berbentuk .ipynb BUKAN .py), yang bisa dibuat misalnya menggunakan Jupyter Notebook atau Google Colaboratory.
Harap sertakan penjelasan untuk setiap variabel yang digunakan dan setiap proses secara singkat di samping potongan kode (dengan comment, ‘#’). Selain itu, sertakan juga penjelasan program (yang bisa mencakupi idenya apa, bagaimana cara eksekusi program, atau tentang algoritma program yang digunakan) pada cell di sebelah (atas/bawah) program.
Format nama file untuk Tugas 1 ini adalah:
Nama Lengkap_NPM_Kelas SIAK_Tugas1PrakMetnum.ipynb
Contoh penamaan yang benar:
Luthfi Athallah Herdita Wiryaman_2206826980_Kelas G_Tugas1PrakMetnum_OnSite.ipynb
Luthfi Athallah Herdita Wiryaman_2206826980_Kelas G_Tugas1PrakMetnum_OnSite_revisi1.ipynb
Pengumpulan tugas dilakukan ke Google Forms berikut ini, sesuai dengan kelas Anda di SIAK NG (link akan selalu sama untuk semua tugas praktikum metode numerik):
Durasi pengerjaan Tugas 1 On-Site ini adalah 1 (satu) hari, dan tenggat waktu (deadline) pengumpulan Tugas 1 On-Site ini adalah pukul 23.59 WIB. Mohon manfaatkan waktu Anda dengan baik (seperti mencicil pengerjaan, bahkan sudah selesai dari jauh-jauh hari) agar mengumpulkan tugas sebelum deadline. Keterlambatan pengumpulan bisa dikenakan pengurangan nilai atau bahkan dianggap tidak mengumpulkan, tergantung kesepakatan dari dosen. Meskipun demikian, lebih baik terlambat mengumpulkan daripada tidak mengumpulkan sama sekali.
Sesuai standar Universitas Indonesia, plagiarisme dilarang keras dan bisa menyebabkan nilai tugas praktikum menjadi nol untuk semua pihak yang terlibat, tanpa peringatan apapun.
Module atau package Python yang boleh digunakan (di-import) untuk Tugas 1 On-Site ini hanyalah numpy, tabulate, dan sympy. Apabila Anda berniat ingin menggunakan module lain, harap konfirmasikan ke narahubung terlebih dahulu (bisa saja diperbolehkan). Narahubung untuk Tugas 1 Praktikum Metode Numerik adalah:
Soal:
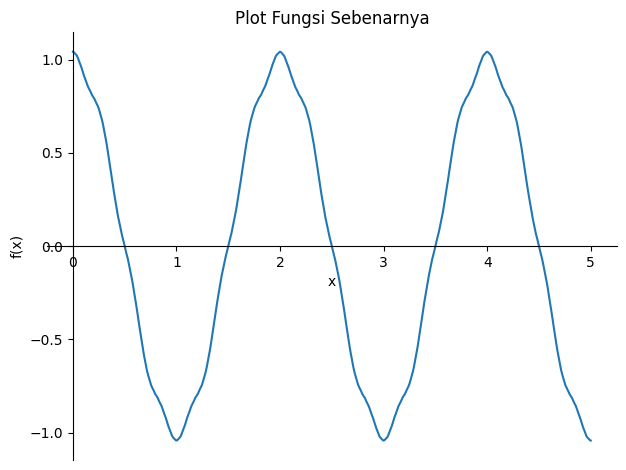
Diberikan suatu fungsi yang berbentuk sebagai berikut:
\[\begin{align*}
∑^6_{i=0}(ae^{-c})^i\cos(7^i \pi x)
\end{align*}\] di mana nilai \(a\) dan \(c\) diberikan pada sesi praktikum Anda.
Berikut adalah hal yang perlu Anda lakukan.
- [10] Pada interval [0, 5] cari nilai \(f(x)\) di mana \(x\) adalah kelipatan dari 0.25! Contoh: \((x, y) = (1.25, 1000)\)
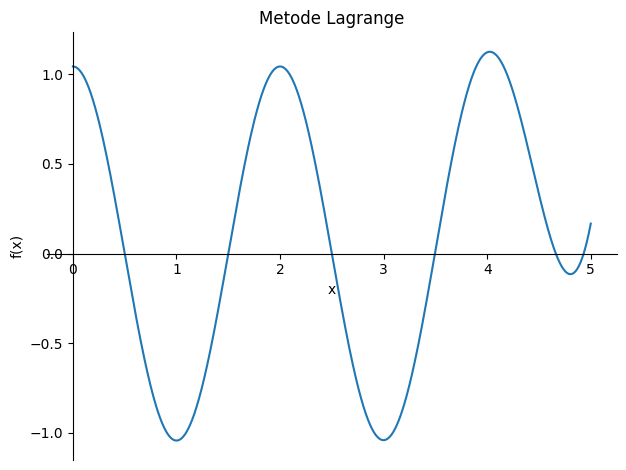
- [30] Gunakan Metode Lagrange untuk menebak fungsi polinomial yang cocok dengan titik-titik yang telah dihasilkan!
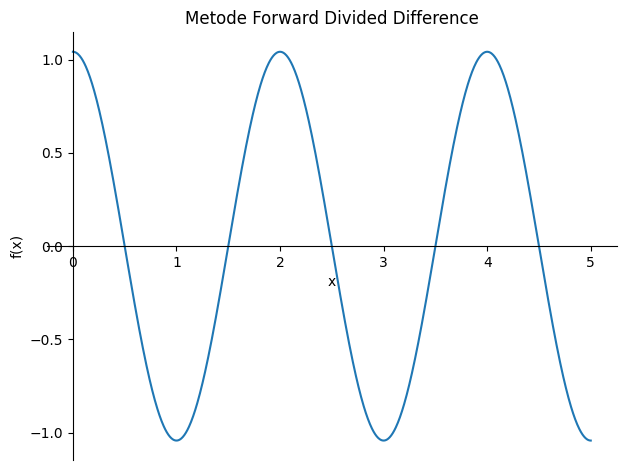
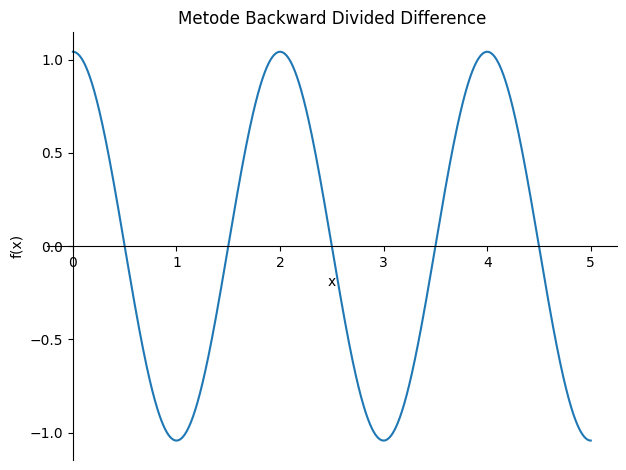
- [30] Gunakan Metode Divided Difference untuk menebak fungsi polinomial yang cocok dengan titik-titik yang telah dihasilkan (bebas menggunakan forward maupun backward)!
- [10] Buatlah plot pada dua bidang yang berbeda fungsi polinomial yang Anda dapatkan dari kedua Metode tadi!
- [10] Aproksimasikan nilai fungsi pada titik yang diberikan pada waktu praktikum menggunakan fungsi yang didapatkan pada dua Metode tadi!
- [10] Menggunakan Metode Neville, cari nilai aproksimasi fungsi pada titik 0.11!
Contoh Output Program:
Berikut adalah titik-titik yang didapatkan menggunakan parameter a dan c yang sudah diberikan
(0.0, 1.04)
(0.25, 0.74)
(0.5, 0.00)
(0.75, -0.74)
(1.0, -1.04)
(1.25, -0.74)
(1.5, -0.00)
(1.75, 0.74)
(2.0, 1.04)
(2.25, 0.74)
(2.5, 0.00)
(2.75, -0.74)
(3.0, -1.04)
(3.25, -0.74)
(3.5, -0.00)
(3.75, 0.74)
(4.0, 1.04)
(4.25, 0.74)
(4.5, 0.00)
(4.75, -0.74)
(5.0, -1.04)
Berikut adalah hasil tebakan fungsi menggunakan Metode Lagrange.
20 19 18 ↪
- 6.47446044497178e-17⋅x + 1.35264783312149e-8⋅x - 6.42507582329925e-7⋅x + 1.37219064397518e ↪
↪ 17 16 15 14 ↪
↪ -5⋅x - 0.000173582451748894⋅x + 0.00144601409105694⋅x - 0.00839415652149755⋅x + 0.035500 ↪
↪ 13 12 11 10 ↪
↪ 6263956135⋅x - 0.115336532015291⋅x + 0.304263569975504⋅x - 0.650473643340547⋅x + 1.01121 ↪
↪ 9 8 7 6 ↪
↪ 459478929⋅x - 1.04614835992595⋅x + 1.28524894381763⋅x - 2.37116713296643⋅x + 0.5562068401538 ↪
↪ 5 4 3 2 ↪
↪ 91⋅x + 4.00468827030339⋅x + 0.0612160233563763⋅x - 5.15342702114251⋅x + 0.000684890859124709 ↪
↪
↪ ⋅x + 1.04231875082799
Berikut adalah hasil tebakan fungsi menggunakan Metode Divided Difference.
Polinom hasil Foward Divided Difference:
20 19 18 ↪
- 7.20345015277778e-17⋅x + 1.352647687931e-8⋅x - 6.42507564496455e-7⋅x + 1.37219062203565e-5 ↪
↪ 17 16 15 14 ↪
↪ ⋅x - 0.000173582456200318⋅x + 0.00144601411720817⋅x - 0.00839415638595183⋅x + 0.03550062 ↪
↪ 13 12 11 10 ↪
↪ 5166286⋅x - 0.115336532734401⋅x + 0.304263560637935⋅x - 0.650473634490823⋅x + 1.01121459 ↪
↪ 9 8 7 6 ↪
↪ 351056⋅x - 1.04614829867763⋅x + 1.28524889093643⋅x - 2.37116707039543⋅x + 0.556206829469079⋅ ↪
↪ 5 4 3 2 ↪
↪ x + 4.00468827634438⋅x + 0.0612160202009252⋅x - 5.15342702061354⋅x + 0.000684890790066429⋅x ↪
↪
↪ + 1.04231875082799
Polinom hasil Backward Divided Difference:
20 19 18 ↪
- 7.20345015277778e-17⋅x + 1.352647687931e-8⋅x - 6.42507564496454e-7⋅x + 1.37219062203565e-5 ↪
↪ 17 16 15 14 ↪
↪ ⋅x - 0.000173582456200318⋅x + 0.00144601411720817⋅x - 0.00839415638595183⋅x + 0.03550062 ↪
↪ 13 12 11 10 ↪
↪ 5166286⋅x - 0.115336532734401⋅x + 0.304263560637936⋅x - 0.650473634490823⋅x + 1.01121459 ↪
↪ 9 8 7 6 ↪
↪ 351055⋅x - 1.04614829867764⋅x + 1.28524889093642⋅x - 2.37116707039513⋅x + 0.556206829467498⋅ ↪
↪ 5 4 3 2 ↪
↪ x + 4.00468827634613⋅x + 0.0612160201999213⋅x - 5.15342702061224⋅x + 0.000684890791792559⋅x ↪
↪
↪ + 1.04231875082758
Tabel Metode Neville:
| i | x_i | Q_{i,0} | Q_{i,1} | Q_{i,2} | Q_{i,3} | Q_{i,4} | Q_{i,5} | Q_{i,6} | Q_{i,7} | Q_{i,8} | Q_{i,9} | Q_{i,10} | Q_{i,11} | Q_{i,12} | Q_{i,13} | Q_{i,14} | Q_{i,15} | Q_{i,16} | Q_{i,17} | Q_{i,18} | Q_{i,19} | Q_{i,20} |
|-----+-------+--------------+---------------------+---------------------+---------------------+---------------------+---------------------+---------------------+--------------------+---------------------+---------------------+---------------------+---------------------+--------------------+---------------------+---------------------+--------------------+---------------------+--------------------+--------------------+--------------------+--------------------|
| 0 | 0 | 1.04232 | | | | | | | | | | | | | | | | | | | | |
| 1 | 0.25 | 0.737031 | 0.9079919894857508 | | | | | | | | | | | | | | | | | | | |
| 2 | 0.5 | 5.93437e-17 | 1.1497678247146421 | 0.9611826732361068 | | | | | | | | | | | | | | | | | | |
| 3 | 0.75 | -0.737031 | 1.1497678247146421 | 1.1497678247146421 | 0.9888418287862919 | | | | | | | | | | | | | | | | | |
| 4 | 1 | -1.04232 | 0.04450686366828194 | 2.011871374330803 | 0.9888418287862922 | 0.9888418287862919 | | | | | | | | | | | | | | | | |
| 5 | 1.25 | -0.737031 | -2.1291443653242523 | 2.826780436778726 | 1.5881186618578829 | 0.9049430721562695 | 0.9814587382028499 | | | | | | | | | | | | | | | |
| 6 | 1.5 | -2.53426e-16 | -4.097890452188084 | 1.3752236692933684 | 4.0654422116995645 | 0.6219624774196271 | 0.9366368987667734 | 0.978171803310871 | | | | | | | | | | | | | | |
| 7 | 1.75 | 0.737031 | -4.097890452188084 | -4.097890452188084 | 7.869985760118024 | 1.6305343407117503 | 0.30728805607248455 | 0.9953761240849069 | 0.9792532177595245 | | | | | | | | | | | | | |
| 8 | 2 | 1.04232 | -1.2656592395067854 | -11.971493223442094 | 7.869985760118009 | 7.869985760118037 | -1.5640647860242685 | 0.7938397950176403 | 1.0114990304102882 | 0.9810267374553164 | | | | | | | | | | | | |
| 9 | 2.25 | 0.737031 | 3.3502967411627544 | -16.405994856102875 | -3.752883530910784 | 21.120056751890836 | -1.5640647860241956 | -1.5640647860242993 | 1.3193156730784155 | 0.9899518654235194 | 0.9814630770448731 | | | | | | | | | | | |
| 10 | 2.5 | 1.8969e-16 | 7.046013079661527 | -10.619511018362601 | -29.05910618129495 | 31.422765953123204 | 11.723985960366923 | -9.448308228882926 | 1.3193156730782842 | 1.3193156730784412 | 0.9694581173916575 | 0.9809348588201316 | | | | | | | | | | |
| 11 | 2.75 | -0.737031 | 7.0460130796615195 | 7.046013079661552 | -55.136631745383475 | 13.708035743810228 | 51.121545945879234 | -18.218159628622427 | -4.988212374158266 | 3.3377246481939804 | 0.9694581173917479 | 0.9694581173916526 | 0.9804757891629925 | | | | | | | | | |
| 12 | 3 | -1.04232 | 2.486811615345296 | 28.838996079093068 | -55.136631745383035 | -55.13663174538432 | 104.03223948963348 | 2.0909699286669743 | -31.44810688308524 | 6.786440682314239 | 2.356756531821996 | 0.7530395647406293 | 0.9804757891629774 | 0.980475789162992 | | | | | | | | |
| 13 | 3.25 | -0.737031 | -4.571449117001265 | 39.75442828213514 | -5.944847874600991 | -160.4070492288566 | 104.03223948962575 | 104.03223948964194 | -78.87952417976456 | -4.41219902397804 | 11.216124832803184 | 0.08875824677081212 | 0.8472467334708944 | 0.9866931450952747 | 0.9806862227483925 | | | | | | | |
| 14 | 3.5 | -2.34471e-16 | -9.994135707134959 | 26.771679373971484 | 85.45370443887118 | -224.38738790379952 | -50.87270941735437 | 299.2124751124207 | -78.87952417970499 | -78.87952417980597 | 33.3179123883081 | 3.3478884630434336 | -0.6697302399253616 | 1.0444537400124076 | 0.9842049963911521 | 0.980796812777165 | | | | | | |
| 15 | 3.75 | 0.737031 | -9.994135707134957 | -9.99413570713498 | 168.4426201531684 | -133.63703304687346 | -397.9020663902422 | 444.2225065306323 | 142.60164118075213 | -260.49407977527983 | 33.317912388064514 | 33.317912388419174 | -6.3515010982599875 | 0.5423808765193585 | 1.1047024836315735 | 0.9793850969015353 | 0.9807554024448132 | | | | | |
| 16 | 4 | 1.04232 | -3.7079639911838047 | -52.61437994128377 | 168.44262015316795 | 168.44262015316968 | -771.6292606053646 | 197.5699297258528 | 745.843371880477 | -427.46179433048775 | -138.79316783281723 | 129.01167299087476 | -6.351501097689678 | -6.351501098429179 | 1.8999453269707631 | 1.0160897096594925 | 0.9780147913585716 | 0.9806800356399415 | | | | |
| 17 | 4.25 | 0.737031 | 5.792601492839768 | -72.87208071487542 | 38.95042755535053 | 575.0481049103146 | -771.6292606053494 | -771.6292606053911 | 1521.2191096639515 | -83.80866754784097 | -716.1304208279109 | 239.94007013196423 | 72.94241043592409 | -36.48318748046291 | 1.899945326189288 | 1.8999453271136613 | 0.924168725444259 | 0.9798994036655726 | 0.9806598310476637 | | | |
| 18 | 4.5 | 7.15028e-16 | 12.942258334608388 | -49.8317287361201 | -184.69458898510126 | 797.1070336274821 | 17.236075972789695 | -2291.5098090792303 | 1521.2191096637155 | 1521.219109664233 | -1610.3684200962134 | -40.08649338107425 | 406.9377298270127 | -81.8087542152803 | -20.584373302711576 | 7.617386348966936 | 0.9241687260507023 | 0.9241687253851306 | 0.9817352377736341 | 0.9806861187676318 | | |
| 19 | 4.75 | -0.737031 | 12.942258334608399 | 12.942258334608297 | -375.4194750096314 | 509.54399614418844 | 1576.9779912821746 | -3247.8236667415226 | -712.2257812826439 | 4469.366365712909 | -1610.3684200941389 | -1610.3684200979887 | 1039.1254489807325 | 61.34177668964586 | -143.0331351253872 | 19.29893769095991 | 4.84496483046727 | 0.2968413493440514 | 0.9817352375394885 | 0.9817352377809185 | 0.9807104141553078 | |
| 20 | 5 | -1.04232 | 4.9291163670223135 | 83.29764481001422 | -375.4194750096324 | -375.4194750096276 | 3086.5576241441004 | -1834.6719789857787 | -5783.4215522004 | 6615.652107693513 | 1951.0577617890003 | -5015.09184997442 | 1039.125448969489 | 1039.1254489878158 | -432.0629071777384 | -28.247025653167707 | 33.75291054757471 | -1.5870530915891354 | 0.5805336886845782 | 1.0165060384402473 | 0.9807104141825383 | 0.9807104141559068 |
Nilai aproksimasi fungsi f(x) = 0.9807104141559068
Terima kasih telah menggunakan program.