import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as snsModul 3 Sains Data: Model Regresi
Regresi Linier Sederhana, Regresi Linier Berganda, dan Regresi Logistik
Kembali ke Sains Data
Pada pertemuan kali ini, kita akan membahas tentang salah satu metode machine learning, yaitu regresi.
Metode regresi yang paling sering digunakan adalah regresi linier (linear regression).
Inti sari dari regresi linier adalah, diberikan sekumpulan data (meliputi satu fitur target yang ingin diprediksi, biasa disebut \(y\), serta minimal satu variabel bebas), ingin ditemukan garis yang paling mendekati semua titik.
“Paling mendekati” bisa diukur dengan menjumlahkan (kuadrat dari) semua selisih antara nilai \(y\) pada tiap titik dengan nilai \(y\) pada garis. (Misalkan fungsi garis ditulis \(y = \hat{y}\left(x\right)\). Maka, nilai \(y\) pada garis ditulis \(\hat{y}\left(x_i\right)\) untuk titik ke-\(i\).)
Jika hasil jumlah ini makin kecil, maka garis makin mendekati titik-titiknya. Hasil jumlah ini disebut error, atau di sini lebih tepatnya SSE (sum of squared errors):
\[\text{SSE = } \sum_{i=1}^{n} \left( y_i - \hat{y}\left(x_i\right) \right)^2\]
Maka, tujuan dari regresi linier adalah menemukan garis yang meminimalkan error, yaitu meminimalkan SSE. Fungsi yang ingin diminimalkan (di sini SSE) biasa disebut fungsi objektif (objective function) di dunia optimasi, atau seringkali disebut loss function di dunia sains data / pembelajaran mesin (machine learning).
Regresi linier umumnya terbagi lagi menjadi dua jenis, yaitu
- regresi linier sederhana (simple linear regression) ketika hanya ada satu variabel bebas \(x\)
- regresi linier berganda (multiple linear regression) ketika ada sejumlah variabel bebas \(x_1, x_2, \dots, x_n\)
Banyak metode regresi lainnya yang sebenarnya dibangun di atas regresi linier, contohnya regresi polinomial (polynomial regression). Intinya sama: mencoba mencari bentuk fungsi tertentu yang paling cocok dengan sekumpulan data yang diberikan, baik untuk urusan deskripsi maupun prediksi.
Import Dataset
Sebelum mulai, seperti biasa, kita perlu meng-import dataset terlebih dahulu.
Untuk praktikum kali ini, kita akan melanjutkan dataset minggu lalu, California Housing Prices, yang sudah dilakukan imputasi. Silakan download housing_modified.csv berikut:
Kemudian read dengan pandas seperti biasa:
df = pd.read_csv("./housing_modified.csv")df| Unnamed: 0 | longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | median_house_value | <1H OCEAN | INLAND | ISLAND | NEAR BAY | NEAR OCEAN | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | -122.23 | 37.88 | 41.0 | 880.0 | 129.0 | 322.0 | 126.0 | 8.3252 | 452600.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 1 | 1 | -122.22 | 37.86 | 21.0 | 7099.0 | 1106.0 | 2401.0 | 1138.0 | 8.3014 | 358500.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 2 | 2 | -122.24 | 37.85 | 52.0 | 1467.0 | 190.0 | 496.0 | 177.0 | 7.2574 | 352100.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 3 | 3 | -122.25 | 37.85 | 52.0 | 1274.0 | 235.0 | 558.0 | 219.0 | 5.6431 | 341300.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 4 | 4 | -122.25 | 37.85 | 52.0 | 1627.0 | 280.0 | 565.0 | 259.0 | 3.8462 | 342200.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 20635 | 20635 | -121.09 | 39.48 | 25.0 | 1665.0 | 374.0 | 845.0 | 330.0 | 1.5603 | 78100.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 20636 | 20636 | -121.21 | 39.49 | 18.0 | 697.0 | 150.0 | 356.0 | 114.0 | 2.5568 | 77100.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 20637 | 20637 | -121.22 | 39.43 | 17.0 | 2254.0 | 485.0 | 1007.0 | 433.0 | 1.7000 | 92300.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 20638 | 20638 | -121.32 | 39.43 | 18.0 | 1860.0 | 409.0 | 741.0 | 349.0 | 1.8672 | 84700.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 20639 | 20639 | -121.24 | 39.37 | 16.0 | 2785.0 | 616.0 | 1387.0 | 530.0 | 2.3886 | 89400.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
20640 rows × 15 columns
df = df.drop(df.columns[0], axis=1)df| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | median_house_value | <1H OCEAN | INLAND | ISLAND | NEAR BAY | NEAR OCEAN | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -122.23 | 37.88 | 41.0 | 880.0 | 129.0 | 322.0 | 126.0 | 8.3252 | 452600.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 1 | -122.22 | 37.86 | 21.0 | 7099.0 | 1106.0 | 2401.0 | 1138.0 | 8.3014 | 358500.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 2 | -122.24 | 37.85 | 52.0 | 1467.0 | 190.0 | 496.0 | 177.0 | 7.2574 | 352100.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 3 | -122.25 | 37.85 | 52.0 | 1274.0 | 235.0 | 558.0 | 219.0 | 5.6431 | 341300.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 4 | -122.25 | 37.85 | 52.0 | 1627.0 | 280.0 | 565.0 | 259.0 | 3.8462 | 342200.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 20635 | -121.09 | 39.48 | 25.0 | 1665.0 | 374.0 | 845.0 | 330.0 | 1.5603 | 78100.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 20636 | -121.21 | 39.49 | 18.0 | 697.0 | 150.0 | 356.0 | 114.0 | 2.5568 | 77100.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 20637 | -121.22 | 39.43 | 17.0 | 2254.0 | 485.0 | 1007.0 | 433.0 | 1.7000 | 92300.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 20638 | -121.32 | 39.43 | 18.0 | 1860.0 | 409.0 | 741.0 | 349.0 | 1.8672 | 84700.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 20639 | -121.24 | 39.37 | 16.0 | 2785.0 | 616.0 | 1387.0 | 530.0 | 2.3886 | 89400.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
20640 rows × 14 columns
Pastikan sudah tidak ada missing value:
df.isna().sum()longitude 0
latitude 0
housing_median_age 0
total_rooms 0
total_bedrooms 0
population 0
households 0
median_income 0
median_house_value 0
<1H OCEAN 0
INLAND 0
ISLAND 0
NEAR BAY 0
NEAR OCEAN 0
dtype: int64Untuk dataset ini, fitur target utama yang ingin diprediksi adalah harga rumah, yaitu median_house_value. Kita bisa memisahkan antara fitur target tersebut, misal \(y\), dengan fitur-fitur lainnya, misal \(X\) besar.
X = df.drop(columns=["median_house_value"])
y = df[["median_house_value"]]X| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | <1H OCEAN | INLAND | ISLAND | NEAR BAY | NEAR OCEAN | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -122.23 | 37.88 | 41.0 | 880.0 | 129.0 | 322.0 | 126.0 | 8.3252 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 1 | -122.22 | 37.86 | 21.0 | 7099.0 | 1106.0 | 2401.0 | 1138.0 | 8.3014 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 2 | -122.24 | 37.85 | 52.0 | 1467.0 | 190.0 | 496.0 | 177.0 | 7.2574 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 3 | -122.25 | 37.85 | 52.0 | 1274.0 | 235.0 | 558.0 | 219.0 | 5.6431 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 4 | -122.25 | 37.85 | 52.0 | 1627.0 | 280.0 | 565.0 | 259.0 | 3.8462 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 20635 | -121.09 | 39.48 | 25.0 | 1665.0 | 374.0 | 845.0 | 330.0 | 1.5603 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 20636 | -121.21 | 39.49 | 18.0 | 697.0 | 150.0 | 356.0 | 114.0 | 2.5568 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 20637 | -121.22 | 39.43 | 17.0 | 2254.0 | 485.0 | 1007.0 | 433.0 | 1.7000 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 20638 | -121.32 | 39.43 | 18.0 | 1860.0 | 409.0 | 741.0 | 349.0 | 1.8672 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 20639 | -121.24 | 39.37 | 16.0 | 2785.0 | 616.0 | 1387.0 | 530.0 | 2.3886 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
20640 rows × 13 columns
y| median_house_value | |
|---|---|
| 0 | 452600.0 |
| 1 | 358500.0 |
| 2 | 352100.0 |
| 3 | 341300.0 |
| 4 | 342200.0 |
| ... | ... |
| 20635 | 78100.0 |
| 20636 | 77100.0 |
| 20637 | 92300.0 |
| 20638 | 84700.0 |
| 20639 | 89400.0 |
20640 rows × 1 columns
Train-Test Split
Inti sari dari machine learning adalah membuat “model” yang bisa belajar dari pola, dan kemudian bisa menghasilkan prediksi yang akurat berdasarkan pola tersebut.
Sehingga, untuk menguji apakah model kita sudah bagus, fokus kita adalah menguji seberapa baik model bisa memprediksi.
- Di satu sisi, model machine learning memerlukan data, yang dengan data tersebut, model akan terbentuk dengan “latihan”, mencoba memahami pola yang ada di data tersebut.
- Di sisi lain, untuk menguji kemampuan model memprediksi, perlu ada juga data acuan sehingga hasil prediksi model bisa dibandingkan dengan data aslinya (yaitu data acuan tersebut).
Data untuk “latihan” disebut data training (training data), dan data acuan untuk menguji kemampuan prediksi disebut data testing (test data).
Tentunya, kedua data ini harus saling lepas (tidak memiliki irisan), agar tidak terjadi yang namanya data leakage. Semisal ada data training yang sama persis muncul di data testing, kan prediksinya jadi hafalan doang, kegampangan :D
Sebenarnya, regresi tidak terbatas machine learning. Kebetulan, regresi juga menjadi pembahasan yang mendalam di kalangan statistika, hingga ada mata kuliah tersendiri yang membahas regresi (Model Linier / Model Linear).
Dalam konteks machine learning, regresi linier (sebagai model) mencoba mencari garis yang meminimalkan SSE menggunakan data training saja, yaitu data yang dimaksudkan untuk membentuk model. Kemudian, garis yang ditemukan (model yang terbentuk) akan diuji kemampuan prediksinya menggunakan data testing.
Di dunia nyata, data yang kita peroleh biasanya utuh, satu kesatuan. Padahal, untuk menggunakan machine learning, kita memerlukan data training dan data testing.
Sehingga, dataset yang utuh tersebut bisa kita pecah sendiri menjadi data training dan data testing, namanya train-test split.
Kebetulan, scikit-learn menyediakan fungsi untuk melakukan train-test split. Mari kita coba. Import dulu:
from sklearn.model_selection import train_test_splitBiasanya, dataset dipisah menjadi data training sebanyak 80% dan data testing sebanyak 20%. Dalam penggunaan fungsi train_test_split, ditulis test_size=0.2.
Rasio 80-20 ini sebenarnya hanya kebiasaan saja; paling sering begitu, tapi boleh saja misalnya 70-30 atau bahkan 90-10.
Mengapa jauh lebih banyak data training? Tujuannya agar model bisa memahami pola pada data dengan lebih mendalam. Namun, perlu hati-hati juga: kalau data testing terlalu sedikit, kita kurang bisa menguji kemampuan prediksi model.
Kalau ragu, langsung gunakan saja rasio 80-20. Sepertinya memang sudah standar, digunakan di mana-mana.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)Apa itu random state?
Tentunya, kita berharap bahwa train-test split dilakukan secara random atau sembarang, yaitu tidak berdasarkan pola tertentu, agar apapun pola yang terkandung dalam data training itu kurang lebih juga terkandung dalam data testing.
Di sisi lain, apabila orang lain ingin mencoba model yang kita buat, tentunya kita juga berharap bahwa dia mendapatkan hasil yang sama.
Apabila train-test split benar-benar selalu random tiap kali dijalankan, kemungkinan hasil yang diperoleh orang lain akan cukup berbeda dengan hasil yang kita peroleh, padahal modelnya sama.
Oleh karena itu, meskipun kita menginginkan train-test split dilakukan secara random, kita juga menginginkan cara random tersebut adalah selalu cara yang sama. Hal ini bisa kita atur dengan memasang nilai random_state yang selalu sama.
Biasanya, random_state dipasang nilai 42. Namun, itu hanya kebiasaan saja. Apapun boleh, asalkan konsisten.
Mari kita lihat hasilnya:
X_train| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | <1H OCEAN | INLAND | ISLAND | NEAR BAY | NEAR OCEAN | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 14196 | -117.03 | 32.71 | 33.0 | 3126.0 | 627.0 | 2300.0 | 623.0 | 3.2596 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 8267 | -118.16 | 33.77 | 49.0 | 3382.0 | 787.0 | 1314.0 | 756.0 | 3.8125 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 17445 | -120.48 | 34.66 | 4.0 | 1897.0 | 331.0 | 915.0 | 336.0 | 4.1563 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 14265 | -117.11 | 32.69 | 36.0 | 1421.0 | 367.0 | 1418.0 | 355.0 | 1.9425 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 2271 | -119.80 | 36.78 | 43.0 | 2382.0 | 431.0 | 874.0 | 380.0 | 3.5542 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 11284 | -117.96 | 33.78 | 35.0 | 1330.0 | 201.0 | 658.0 | 217.0 | 6.3700 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 11964 | -117.43 | 34.02 | 33.0 | 3084.0 | 570.0 | 1753.0 | 449.0 | 3.0500 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 5390 | -118.38 | 34.03 | 36.0 | 2101.0 | 569.0 | 1756.0 | 527.0 | 2.9344 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 860 | -121.96 | 37.58 | 15.0 | 3575.0 | 597.0 | 1777.0 | 559.0 | 5.7192 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 15795 | -122.42 | 37.77 | 52.0 | 4226.0 | 1315.0 | 2619.0 | 1242.0 | 2.5755 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
16512 rows × 13 columns
X_test| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | <1H OCEAN | INLAND | ISLAND | NEAR BAY | NEAR OCEAN | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 20046 | -119.01 | 36.06 | 25.0 | 1505.0 | 537.870553 | 1392.0 | 359.0 | 1.6812 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 3024 | -119.46 | 35.14 | 30.0 | 2943.0 | 537.870553 | 1565.0 | 584.0 | 2.5313 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 15663 | -122.44 | 37.80 | 52.0 | 3830.0 | 537.870553 | 1310.0 | 963.0 | 3.4801 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 20484 | -118.72 | 34.28 | 17.0 | 3051.0 | 537.870553 | 1705.0 | 495.0 | 5.7376 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 9814 | -121.93 | 36.62 | 34.0 | 2351.0 | 537.870553 | 1063.0 | 428.0 | 3.7250 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 15362 | -117.22 | 33.36 | 16.0 | 3165.0 | 482.000000 | 1351.0 | 452.0 | 4.6050 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 16623 | -120.83 | 35.36 | 28.0 | 4323.0 | 886.000000 | 1650.0 | 705.0 | 2.7266 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 18086 | -122.05 | 37.31 | 25.0 | 4111.0 | 538.000000 | 1585.0 | 568.0 | 9.2298 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2144 | -119.76 | 36.77 | 36.0 | 2507.0 | 466.000000 | 1227.0 | 474.0 | 2.7850 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 3665 | -118.37 | 34.22 | 17.0 | 1787.0 | 463.000000 | 1671.0 | 448.0 | 3.5521 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 |
4128 rows × 13 columns
y_train| median_house_value | |
|---|---|
| 14196 | 103000.0 |
| 8267 | 382100.0 |
| 17445 | 172600.0 |
| 14265 | 93400.0 |
| 2271 | 96500.0 |
| ... | ... |
| 11284 | 229200.0 |
| 11964 | 97800.0 |
| 5390 | 222100.0 |
| 860 | 283500.0 |
| 15795 | 325000.0 |
16512 rows × 1 columns
y_test| median_house_value | |
|---|---|
| 20046 | 47700.0 |
| 3024 | 45800.0 |
| 15663 | 500001.0 |
| 20484 | 218600.0 |
| 9814 | 278000.0 |
| ... | ... |
| 15362 | 263300.0 |
| 16623 | 266800.0 |
| 18086 | 500001.0 |
| 2144 | 72300.0 |
| 3665 | 151500.0 |
4128 rows × 1 columns
Regresi Linier Sederhana
Untuk satu variabel bebas \(x\), rumus garis untuk regresi linier sederhana adalah sebagai berikut:
\[y = \beta_0 + \beta_1 x + \varepsilon \sim NIID(0, \sigma^2)\]
Ingin ditemukan nilai \(\beta_0\) dan \(\beta_1\) yang meminimalkan SSE.
(Ada juga yang menulis \(y = \theta_0 + \theta_1 x\), sama saja)
\(\varepsilon\) merupakan error dari model regresi. Error ini bersifat random dan diasumsikan mengikuti Normal Identic Independent Distribution (NIID) - Error berdistribusi normal, artinya memiliki pola sebaran probabilitas yang sesuai dengan distribusi normal dengan mean 0 dan variansi suatu konstan \(\sigma^2\). - Identik berarti error dari setiap observasi (baris) berdistribusi sama (yaitu normal dengan parameter yang sama) - Independen artinya error dari setiap observasi saling bebas, atau Cov \((\varepsilon_i, \varepsilon_j)=0\) untuk setiap observasi ke \(i\neq j\)
Perlu diperhatikan juga bahwa model yang dibangun diatas merupakan model untuk populasi data (jadi bisa dibilang kita mengasumsikan seluruh populasi data mengikuti model tersebut). Pada kenyataannya, kita tidak punya data yang mencakup keseluruhan populasi untuk memeriksa apakah modelnya berlaku. Sehingga kita perlu membuat model yang hanya digunakan untuk data sampel yang kita punya. Secara statistik, kita menyebut model tersebut sebagai model taksiran (dugaan) yang akan di fit dengan data sampel yang kita miliki, yaitu
\[\hat{y}=\hat{\beta}_0+\hat{\beta}_1x+e\]
Jadi tujuan kita sekarang adalah mencari taksiran untuk parameter \(\hat{\beta}_0\) dan \(\hat{\beta}_1\) tersebut kemudian melakukan prediksi dengan menggunakan model taksiran yang didapat. Setelah itu kita bandingkan hasil prediksi model dengan nilai aslinya menggunakan metrik evaluasi.
Mari kita pilih terlebih dahulu, variabel bebas apa yang ingin kita gunakan.
df| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | median_house_value | <1H OCEAN | INLAND | ISLAND | NEAR BAY | NEAR OCEAN | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -122.23 | 37.88 | 41.0 | 880.0 | 129.0 | 322.0 | 126.0 | 8.3252 | 452600.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 1 | -122.22 | 37.86 | 21.0 | 7099.0 | 1106.0 | 2401.0 | 1138.0 | 8.3014 | 358500.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 2 | -122.24 | 37.85 | 52.0 | 1467.0 | 190.0 | 496.0 | 177.0 | 7.2574 | 352100.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 3 | -122.25 | 37.85 | 52.0 | 1274.0 | 235.0 | 558.0 | 219.0 | 5.6431 | 341300.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 4 | -122.25 | 37.85 | 52.0 | 1627.0 | 280.0 | 565.0 | 259.0 | 3.8462 | 342200.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 20635 | -121.09 | 39.48 | 25.0 | 1665.0 | 374.0 | 845.0 | 330.0 | 1.5603 | 78100.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 20636 | -121.21 | 39.49 | 18.0 | 697.0 | 150.0 | 356.0 | 114.0 | 2.5568 | 77100.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 20637 | -121.22 | 39.43 | 17.0 | 2254.0 | 485.0 | 1007.0 | 433.0 | 1.7000 | 92300.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 20638 | -121.32 | 39.43 | 18.0 | 1860.0 | 409.0 | 741.0 | 349.0 | 1.8672 | 84700.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 20639 | -121.24 | 39.37 | 16.0 | 2785.0 | 616.0 | 1387.0 | 530.0 | 2.3886 | 89400.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
20640 rows × 14 columns
Sebelum membangun model, kita perlu menentukan fitur mana saja yang ingin kita gunakan sebagai prediktor. Dalam regresi linier sederhana, kita hanya menggunakan satu prediktor, sehingga untuk mendapatkan model yang bagus, kita harus pilih dengan baik fitur mana yang paling memiliki hubungan dengan variabel target. Cara paling sederhana adalah kita bisa melihat korelasi antar setiap fitur prediktor dengan variabel target.
corr = df.corr()
plt.figure(figsize=(14,10))
sns.heatmap(data=corr, vmin=-1, vmax=1, center=0, annot=True)
plt.show()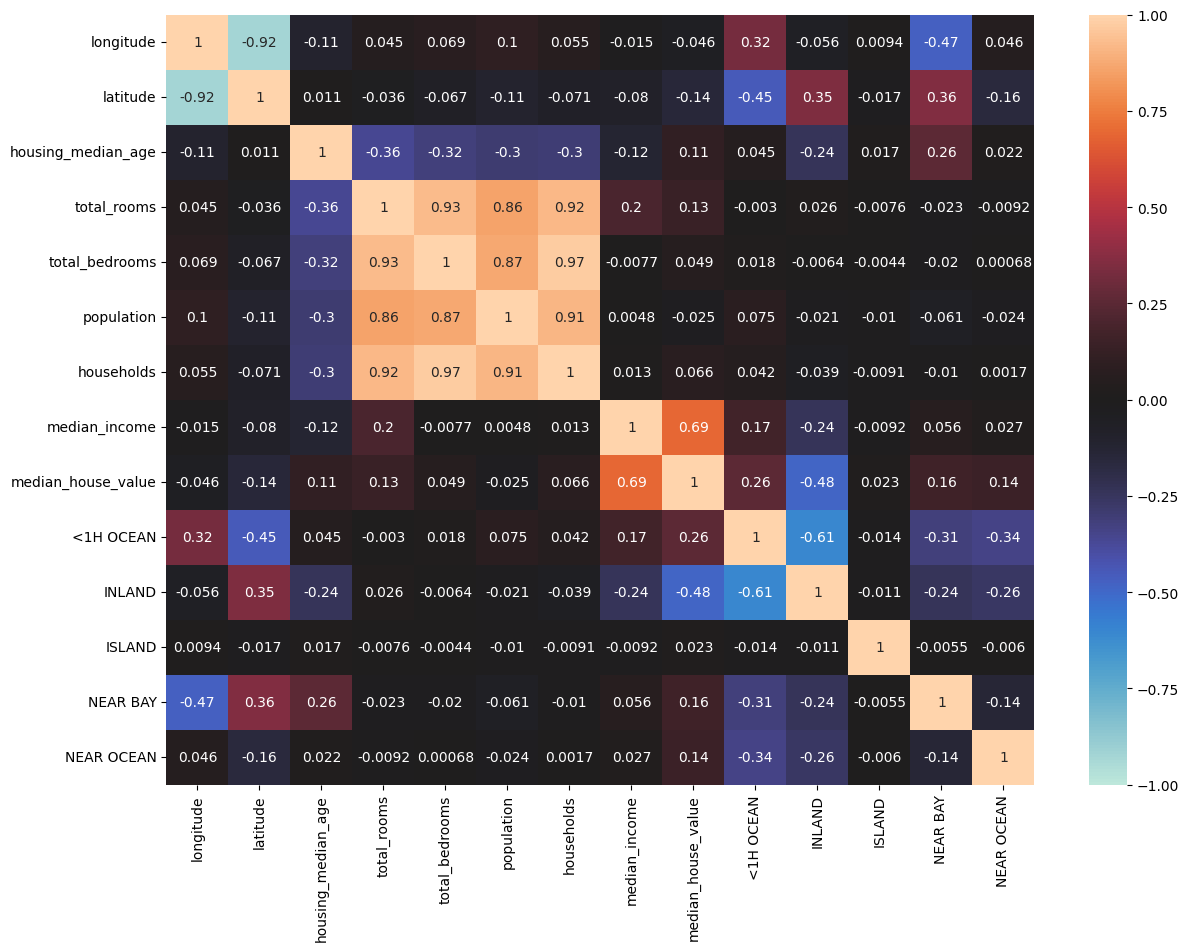
Dari heatmap diatas, kita bisa lihat bahwa fitur median_income memiliki korelasi paling tinggi dengan target median_house_value. Kita bisa coba menggunakan fitur median_income sebagai prediktor untuk mencoba memprediksi variabel target median_house_value. (Asumsinya, mungkin harga rumah kurang lebih berbanding lurus dengan penghasilan.)
x1_train = X_train[["median_income"]]
x1_test = X_test[["median_income"]]x1_train| median_income | |
|---|---|
| 14196 | 3.2596 |
| 8267 | 3.8125 |
| 17445 | 4.1563 |
| 14265 | 1.9425 |
| 2271 | 3.5542 |
| ... | ... |
| 11284 | 6.3700 |
| 11964 | 3.0500 |
| 5390 | 2.9344 |
| 860 | 5.7192 |
| 15795 | 2.5755 |
16512 rows × 1 columns
x1_test| median_income | |
|---|---|
| 20046 | 1.6812 |
| 3024 | 2.5313 |
| 15663 | 3.4801 |
| 20484 | 5.7376 |
| 9814 | 3.7250 |
| ... | ... |
| 15362 | 4.6050 |
| 16623 | 2.7266 |
| 18086 | 9.2298 |
| 2144 | 2.7850 |
| 3665 | 3.5521 |
4128 rows × 1 columns
Ada beberapa cara untuk melakukan regresi linier sederhana di Python.
Regresi Linier Sederhana dengan scikit-learn
from sklearn.linear_model import LinearRegressionLinearRegression adalah class yang dapat menghasilkan objek (inget-inget lagi materi OOP di praktikum Struktur Data :D), dengan tiap objek itu adalah model regresi linier tersendiri.
Sehingga, untuk membuat model regresi linier, kita buat objeknya terlebih dahulu:
linreg1 = LinearRegression()Training dilakukan dengan method .fit()
linreg1.fit(x1_train, y_train)LinearRegression()In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
LinearRegression()
Setelah dilakukan .fit(), model linreg1 sudah selesai training.
Kita bisa memperoleh nilai parameter \(\beta_0\) dan \(\beta_1\) melalui atribut .intercept_ dan .coef_
linreg1.intercept_array([44459.72916908])linreg1.coef_array([[41933.84939381]])linreg1_b0 = linreg1.intercept_[0]
linreg1_b1 = linreg1.coef_[0][0]Taksiran model regresi linier sederhana yang didapat (dalam bentuk \(\hat{y}=\hat{\beta_0}+\hat{\beta_1}x\))
print("y =", linreg1_b0, "+", linreg1_b1, "x")y = 44459.729169078666 + 41933.84939381274 xSetelah kita dapat taksirannya, kita bisa coba lakukan prediksi dengan method .predict()
y_pred1 = linreg1.predict(x1_test)y_pred1array([[114958.91676996],
[150606.88213964],
[190393.71844449],
...,
[431500.77230409],
[161245.49973085],
[193412.95560084]])Solusi Manual dengan Metode Least Squares
Metode least squares menyediakan “solusi eksak” (dijamin meminimalkan loss function) untuk regresi linier sederhana, sebagai berikut:
\[\hat{\beta}_1 = \frac{n \left( \sum_{i=1}^{n} x_i y_i \right) - \left( \sum_{i=1}^{n} x_i \right) \left( \sum_{i=1}^{n} y_i \right)}{n \left( \sum_{i=1}^{n} \left(x_i\right)^2 \right) - \left( \sum_{i=1}^{n} x_i \right)^2}\]
\[\hat{\beta}_0 = \bar{y} - \beta_1 \bar{x}\]
dengan
\[\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i\]
\[\bar{y} = \frac{1}{n} \sum_{i=1}^{n} y_i\]
def least_squares_sederhana(x, y):
n = len(y)
x = np.array(x)
y = np.array(y)
sum_x = sum(x)
sum_y = sum(y)
sum_x2 = sum(x**2)
sum_xy = sum(x*y)
atas = n*(sum_xy) - (sum_x)*(sum_y)
bawah = n * sum_x2 - (sum_x)**2
beta1 = atas/bawah
mean_x = sum_x / n
mean_y = sum_y / n
beta0 = mean_y - beta1 * mean_x
return (beta0[0], beta1[0])linreg2_betas = least_squares_sederhana(x1_train, y_train)linreg2_betas(44459.72916908396, 41933.849393811244)linreg2_beta0, linreg2_beta1 = linreg2_betasUntuk melakukan prediksi, ikuti rumus model (bentuk umum) \(y = \beta_0 + \beta_1 x\):
y_pred2 = np.array(linreg2_beta0 + linreg2_beta1 * x1_test)y_pred2array([[114958.91676996],
[150606.88213964],
[190393.71844449],
...,
[431500.77230408],
[161245.49973085],
[193412.95560084]])Regresi Linier Sederhana dengan statsmodels
scikit-learn adalah package di Python untuk kebutuhan sains data dan/atau machine learning dasar.
Karena regresi linier juga dibahas di dunia statistika, ada package statistika bernama “statsmodels” yang juga menyediakan model regresi linier, yang disebut OLS (ordinary least squares). Bedanya, model regresi linier dari statsmodels menyediakan lebih banyak statistik seputar model. Mari kita coba.
Kalau belum punya, install terlebih dahulu:
!pip install statsmodelsKemudian import:
import statsmodels.api as smSebelum membuat model, statsmodels memerlukan adanya kolom intercept di variabel prediktor, yaitu kolom yang berisi konstanta yaitu 1 semua.
x1_train_sm = sm.add_constant(x1_train)Model OLS bisa diakses melalui sm.OLS, yang lagi-lagi merupakan class
linreg3_OLS = sm.OLS(y_train, x1_train_sm)Agak berbeda dengan scikit-learn, statsmodels menghasilkan objek baru lagi (yang menyimpan hasilnya) ketika dilakukan training dengan .fit()
linreg3 = linreg3_OLS.fit()Kita bisa lihat hasilnya:
print(linreg3.summary()) OLS Regression Results
==============================================================================
Dep. Variable: median_house_value R-squared: 0.477
Model: OLS Adj. R-squared: 0.477
Method: Least Squares F-statistic: 1.506e+04
Date: Mon, 17 Mar 2025 Prob (F-statistic): 0.00
Time: 14:07:10 Log-Likelihood: -2.1058e+05
No. Observations: 16512 AIC: 4.212e+05
Df Residuals: 16510 BIC: 4.212e+05
Df Model: 1
Covariance Type: nonrobust
=================================================================================
coef std err t P>|t| [0.025 0.975]
---------------------------------------------------------------------------------
const 4.446e+04 1477.242 30.096 0.000 4.16e+04 4.74e+04
median_income 4.193e+04 341.735 122.709 0.000 4.13e+04 4.26e+04
==============================================================================
Omnibus: 3353.131 Durbin-Watson: 1.982
Prob(Omnibus): 0.000 Jarque-Bera (JB): 7339.541
Skew: 1.175 Prob(JB): 0.00
Kurtosis: 5.268 Cond. No. 10.2
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.Parameter \(\hat{\beta}_0\) dan \(\hat{\beta}_1\) bisa diperoleh melalui atribut .params
linreg3_betas = linreg3.paramslinreg3_betasconst 44459.729169
median_income 41933.849394
dtype: float64linreg3_beta0 = linreg3_betas["const"]
linreg3_beta1 = linreg3_betas["median_income"]print("y =", linreg3_beta0, "+", linreg3_beta1, "x")y = 44459.72916907856 + 41933.849393812736 xPrediksi dengan .predict()
x1_test_sm = sm.add_constant(x1_test)y_pred3 = linreg3.predict(x1_test_sm)y_pred320046 114958.916770
3024 150606.882140
15663 190393.718444
20484 285059.383451
9814 200663.318161
...
15362 237565.105628
16623 158796.562926
18086 431500.772304
2144 161245.499731
3665 193412.955601
Length: 4128, dtype: float64Metrik Evaluasi untuk Regresi
Setelah kita mendapat hasil prediksi, metrik evaluasi dalam regresi digunakan untuk mengukur seberapa baik model regresi dalam memprediksi nilai variabel dependen. Metrik ini membandingkan nilai sebenarnya (\(y_i\)) dengan nilai prediksi (\(\hat{y}_i\)) dari model. Ada beberapa metrik evaluasi yang bisa digunakan, yaitu
Mean Absolute Error (MAE): rata-rata error absolut antara nilai aktual dan prediksi. \[MAE = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i|\]
Mean Squared Error (MSE): rata-rata kuadrat error antara nilai aktual dan prediksi. \[MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2\]
Koefisien Determinasi (\(R^2\)): Ukuran seberapa baik model dalam menjelaskan variasi dalam data. \[R^2 = 1 - \frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{\sum_{i=1}^{n} (y_i - \bar{y})^2}\]
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_scoremean_absolute_error(y_test, y_pred1)62990.86530093761mean_squared_error(y_test, y_pred1)7091157771.76555r2_score(y_test, y_pred1)0.45885918903846656MAE dan MSE mengukur seberapa besar error dari model. Semakin kecil nilai MSE atau MAE, semakin bagus model taksiran yang dibuat. Dalam kasus ini bisa dibilang hasil MAE dan MSE yang didapat cukup besar, sehingga model masih kurang bagus untuk memprediksi data.
\(R^2\) digunakan untuk mengukur seberapa baik model bisa menjelaskan data. Dalam kasus ini, kita bisa bilang bahwa sebesar \(45.885\%\) variasi dari variabel target median_house_value bisa dijelaskan oleh prediktor median_income menggunakan model linier yang dibangun.
MAE dan MSE digunakan untuk melihat seberapa akurat hasil prediksi yang dilakukan oleh model. Sedangkan \(R^2\) digunakan untuk melihat seberapa bagus model yang dibagun dalam menjelaskan data.
Regresi Linier Berganda
Regresi linier berganda memiliki bentuk umum
\[ y=\beta_0+\beta_1x_1+\beta_2x_2+...+\beta_k x_k+\varepsilon\sim NIID(0, \sigma^2) \]
dimana \(x_1, x_2, ..., x_k\) merupakan variabel prediktor yang digunakan dan \(y\) merupakan variabel target. Tujuan kita masih sama, yaitu ingin mencari taksiran parameter \(\hat{\beta}_1, \hat{\beta}_2, ...,\hat{\beta}_k\) yang meminimalkan SSE.
linreg4 = LinearRegression()Misalkan kita coba menggunakan semua fitur pada dataset sebagai variabel prediktor pada model regresi linier berganda
X_train| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | <1H OCEAN | INLAND | ISLAND | NEAR BAY | NEAR OCEAN | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 14196 | -117.03 | 32.71 | 33.0 | 3126.0 | 627.0 | 2300.0 | 623.0 | 3.2596 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 8267 | -118.16 | 33.77 | 49.0 | 3382.0 | 787.0 | 1314.0 | 756.0 | 3.8125 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 17445 | -120.48 | 34.66 | 4.0 | 1897.0 | 331.0 | 915.0 | 336.0 | 4.1563 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 14265 | -117.11 | 32.69 | 36.0 | 1421.0 | 367.0 | 1418.0 | 355.0 | 1.9425 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 2271 | -119.80 | 36.78 | 43.0 | 2382.0 | 431.0 | 874.0 | 380.0 | 3.5542 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 11284 | -117.96 | 33.78 | 35.0 | 1330.0 | 201.0 | 658.0 | 217.0 | 6.3700 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 11964 | -117.43 | 34.02 | 33.0 | 3084.0 | 570.0 | 1753.0 | 449.0 | 3.0500 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 5390 | -118.38 | 34.03 | 36.0 | 2101.0 | 569.0 | 1756.0 | 527.0 | 2.9344 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 860 | -121.96 | 37.58 | 15.0 | 3575.0 | 597.0 | 1777.0 | 559.0 | 5.7192 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 15795 | -122.42 | 37.77 | 52.0 | 4226.0 | 1315.0 | 2619.0 | 1242.0 | 2.5755 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
16512 rows × 13 columns
y_train| median_house_value | |
|---|---|
| 14196 | 103000.0 |
| 8267 | 382100.0 |
| 17445 | 172600.0 |
| 14265 | 93400.0 |
| 2271 | 96500.0 |
| ... | ... |
| 11284 | 229200.0 |
| 11964 | 97800.0 |
| 5390 | 222100.0 |
| 860 | 283500.0 |
| 15795 | 325000.0 |
16512 rows × 1 columns
linreg4.fit(X_train, y_train)LinearRegression()In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
LinearRegression()
linreg4.intercept_array([-2256620.79885462])linreg4.coef_array([[-2.68382734e+04, -2.54683520e+04, 1.10218508e+03,
-6.02150567e+00, 1.02789395e+02, -3.81729064e+01,
4.82527528e+01, 3.94739752e+04, -1.89265829e+04,
-5.87132390e+04, 1.17198490e+05, -2.40632251e+04,
-1.54954428e+04]])\[\hat{y} = \hat{\beta}_0 + \hat{\beta}_1 x_1 + \hat{\beta}_2 x_2 + \dots + \hat{\beta}_{13} x_{13}\]
y_pred4 = linreg4.predict(X_test)y_pred4array([[ 64629.45079786],
[134799.34083607],
[266063.38139054],
...,
[439180.98341181],
[120797.55240621],
[183386.04993584]])y_test| median_house_value | |
|---|---|
| 20046 | 47700.0 |
| 3024 | 45800.0 |
| 15663 | 500001.0 |
| 20484 | 218600.0 |
| 9814 | 278000.0 |
| ... | ... |
| 15362 | 263300.0 |
| 16623 | 266800.0 |
| 18086 | 500001.0 |
| 2144 | 72300.0 |
| 3665 | 151500.0 |
4128 rows × 1 columns
Metrik evaluasi
mean_absolute_error(y_test, y_pred4)50701.77903133022mean_squared_error(y_test, y_pred4)4904399775.949286r2_score(y_test, y_pred4)0.6257351821159696Bandingkan dengan hasil regresi linier sederhana yang kita coba sebelumnya:
print("Hasil regresi linier sederhana (model linreg1)")
print("MAE:", mean_absolute_error(y_test, y_pred1))
print("MSE", mean_squared_error(y_test, y_pred1))
print("R^2:", r2_score(y_test, y_pred1))
print()
print("Hasil regresi linier berganda (model linreg4)")
print("MAE:", mean_absolute_error(y_test, y_pred4))
print("MSE", mean_squared_error(y_test, y_pred4))
print("R^2:", r2_score(y_test, y_pred4))Hasil regresi linier sederhana (model linreg1)
MAE: 62990.86530093761
MSE 7091157771.76555
R^2: 0.45885918903846656
Hasil regresi linier berganda (model linreg4)
MAE: 50701.77903133022
MSE 4904399775.949286
R^2: 0.6257351821159696Didapatkan ternyata hasil MAE dan MSE dari model regresi linier berganda lebih kecil dibandingkan pada regresi linier sederhana. Artinya model ini lebih bagus dalam melakukan prediksi data (meskipun sebenarnya masih kurang bagus karena nilainya yang sangat besar)
Selain itu, \(R^2\) pada model regresi linier berganda juga lebih tinggi. Sebesar \(62.57\%\) variasi dari variabel target median_house_value bisa dijelaskan oleh semua prediktor menggunakan model regresi linier berganda.
Regresi Logistik
Jika sebelumnya kita memiliki variabel target yang bersifat numerik, bagaimana jika kita memiliki variabel target yang bersifat biner? Dalam membuat model untuk melihat hubungan antara variabel target biner ( y ) dan satu variabel prediktor ( x ) kita bisa menggunakan model regresi logistik (atau logit).
\[ E(y) = \frac{\exp(\beta_0 + \beta_1 x)} {1 + \exp(\beta_0 + \beta_1 x)} \] dimana
\[ y = \begin{cases} 1, & \text{jika kategori A terjadi} \\ 0, & \text{jika kategori B terjadi} \end{cases} \]
\[ E(y) = P(\text{kategori A terjadi}) = \pi \]
dengan \(x\) merupakan variabel prediktor.
Jika kita ambil logit (log odds) dari probabilitas \(\pi\), kita mendapatkan persamaan linear:
\[ \log \left( \frac{\pi}{1 - \pi} \right) = \beta_0 + \beta_1 x \]
dimana: - $ $ adalah probabilitas kejadian. - \(\frac{\pi}{1 - \pi}\) adalah odds (peluang terjadinya kategori A dibanding kategori B). - \(\log(\text{odds})\) disebut logit function, yang mengubah probabilitas menjadi skala linear.
from sklearn.linear_model import LogisticRegressionlogreg1 = LogisticRegression()df.describe()| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | median_house_value | <1H OCEAN | INLAND | ISLAND | NEAR BAY | NEAR OCEAN | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 20640.000000 | 20640.000000 | 20640.000000 | 20640.000000 | 20640.000000 | 20640.000000 | 20640.000000 | 20640.000000 | 20640.000000 | 20640.000000 | 20640.000000 | 20640.000000 | 20640.000000 | 20640.000000 |
| mean | -119.569704 | 35.631861 | 28.639486 | 2635.763081 | 537.870553 | 1425.476744 | 499.539680 | 3.870671 | 206855.816909 | 0.442636 | 0.317393 | 0.000242 | 0.110950 | 0.128779 |
| std | 2.003532 | 2.135952 | 12.585558 | 2181.615252 | 419.266592 | 1132.462122 | 382.329753 | 1.899822 | 115395.615874 | 0.496710 | 0.465473 | 0.015563 | 0.314077 | 0.334963 |
| min | -124.350000 | 32.540000 | 1.000000 | 2.000000 | 1.000000 | 3.000000 | 1.000000 | 0.499900 | 14999.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 25% | -121.800000 | 33.930000 | 18.000000 | 1447.750000 | 297.000000 | 787.000000 | 280.000000 | 2.563400 | 119600.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 50% | -118.490000 | 34.260000 | 29.000000 | 2127.000000 | 438.000000 | 1166.000000 | 409.000000 | 3.534800 | 179700.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 75% | -118.010000 | 37.710000 | 37.000000 | 3148.000000 | 643.250000 | 1725.000000 | 605.000000 | 4.743250 | 264725.000000 | 1.000000 | 1.000000 | 0.000000 | 0.000000 | 0.000000 |
| max | -114.310000 | 41.950000 | 52.000000 | 39320.000000 | 6445.000000 | 35682.000000 | 6082.000000 | 15.000100 | 500001.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
df2 = df.copy()Misalkan kita buat fitur baru yang berisi apakah total ruangan di fitur total_rooms lebih dari \(2000\)
df2[["many_rooms"]] = (df2[["total_rooms"]] >= 2000)df2| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | median_house_value | <1H OCEAN | INLAND | ISLAND | NEAR BAY | NEAR OCEAN | many_rooms | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -122.23 | 37.88 | 41.0 | 880.0 | 129.0 | 322.0 | 126.0 | 8.3252 | 452600.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | False |
| 1 | -122.22 | 37.86 | 21.0 | 7099.0 | 1106.0 | 2401.0 | 1138.0 | 8.3014 | 358500.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | True |
| 2 | -122.24 | 37.85 | 52.0 | 1467.0 | 190.0 | 496.0 | 177.0 | 7.2574 | 352100.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | False |
| 3 | -122.25 | 37.85 | 52.0 | 1274.0 | 235.0 | 558.0 | 219.0 | 5.6431 | 341300.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | False |
| 4 | -122.25 | 37.85 | 52.0 | 1627.0 | 280.0 | 565.0 | 259.0 | 3.8462 | 342200.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | False |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 20635 | -121.09 | 39.48 | 25.0 | 1665.0 | 374.0 | 845.0 | 330.0 | 1.5603 | 78100.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | False |
| 20636 | -121.21 | 39.49 | 18.0 | 697.0 | 150.0 | 356.0 | 114.0 | 2.5568 | 77100.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | False |
| 20637 | -121.22 | 39.43 | 17.0 | 2254.0 | 485.0 | 1007.0 | 433.0 | 1.7000 | 92300.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | True |
| 20638 | -121.32 | 39.43 | 18.0 | 1860.0 | 409.0 | 741.0 | 349.0 | 1.8672 | 84700.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | False |
| 20639 | -121.24 | 39.37 | 16.0 | 2785.0 | 616.0 | 1387.0 | 530.0 | 2.3886 | 89400.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | True |
20640 rows × 15 columns
df2 = df2.drop(columns=["total_rooms"], axis=1)df2| longitude | latitude | housing_median_age | total_bedrooms | population | households | median_income | median_house_value | <1H OCEAN | INLAND | ISLAND | NEAR BAY | NEAR OCEAN | many_rooms | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -122.23 | 37.88 | 41.0 | 129.0 | 322.0 | 126.0 | 8.3252 | 452600.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | False |
| 1 | -122.22 | 37.86 | 21.0 | 1106.0 | 2401.0 | 1138.0 | 8.3014 | 358500.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | True |
| 2 | -122.24 | 37.85 | 52.0 | 190.0 | 496.0 | 177.0 | 7.2574 | 352100.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | False |
| 3 | -122.25 | 37.85 | 52.0 | 235.0 | 558.0 | 219.0 | 5.6431 | 341300.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | False |
| 4 | -122.25 | 37.85 | 52.0 | 280.0 | 565.0 | 259.0 | 3.8462 | 342200.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | False |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 20635 | -121.09 | 39.48 | 25.0 | 374.0 | 845.0 | 330.0 | 1.5603 | 78100.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | False |
| 20636 | -121.21 | 39.49 | 18.0 | 150.0 | 356.0 | 114.0 | 2.5568 | 77100.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | False |
| 20637 | -121.22 | 39.43 | 17.0 | 485.0 | 1007.0 | 433.0 | 1.7000 | 92300.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | True |
| 20638 | -121.32 | 39.43 | 18.0 | 409.0 | 741.0 | 349.0 | 1.8672 | 84700.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | False |
| 20639 | -121.24 | 39.37 | 16.0 | 616.0 | 1387.0 | 530.0 | 2.3886 | 89400.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | True |
20640 rows × 14 columns
Karena many_rooms merupakan fitur biner, kita bisa gunakan sebagai variabel target untuk model regresi logistik
X2 = df2.drop(columns=["many_rooms"], axis=1)
y2 = df2[["many_rooms"]]X2| longitude | latitude | housing_median_age | total_bedrooms | population | households | median_income | median_house_value | <1H OCEAN | INLAND | ISLAND | NEAR BAY | NEAR OCEAN | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -122.23 | 37.88 | 41.0 | 129.0 | 322.0 | 126.0 | 8.3252 | 452600.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 1 | -122.22 | 37.86 | 21.0 | 1106.0 | 2401.0 | 1138.0 | 8.3014 | 358500.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 2 | -122.24 | 37.85 | 52.0 | 190.0 | 496.0 | 177.0 | 7.2574 | 352100.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 3 | -122.25 | 37.85 | 52.0 | 235.0 | 558.0 | 219.0 | 5.6431 | 341300.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 4 | -122.25 | 37.85 | 52.0 | 280.0 | 565.0 | 259.0 | 3.8462 | 342200.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 20635 | -121.09 | 39.48 | 25.0 | 374.0 | 845.0 | 330.0 | 1.5603 | 78100.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 20636 | -121.21 | 39.49 | 18.0 | 150.0 | 356.0 | 114.0 | 2.5568 | 77100.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 20637 | -121.22 | 39.43 | 17.0 | 485.0 | 1007.0 | 433.0 | 1.7000 | 92300.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 20638 | -121.32 | 39.43 | 18.0 | 409.0 | 741.0 | 349.0 | 1.8672 | 84700.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 20639 | -121.24 | 39.37 | 16.0 | 616.0 | 1387.0 | 530.0 | 2.3886 | 89400.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
20640 rows × 13 columns
y2| many_rooms | |
|---|---|
| 0 | False |
| 1 | True |
| 2 | False |
| 3 | False |
| 4 | False |
| ... | ... |
| 20635 | False |
| 20636 | False |
| 20637 | True |
| 20638 | False |
| 20639 | True |
20640 rows × 1 columns
X2_train, X2_test, y2_train, y2_test = train_test_split(X2, y2, test_size=0.2, random_state=42)logreg1.fit(X2_train, y2_train)LogisticRegression()In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
LogisticRegression()
y2_pred = logreg1.predict(X2_test)y2_predarray([ True, True, True, ..., True, True, True])y2_test| many_rooms | |
|---|---|
| 20046 | False |
| 3024 | True |
| 15663 | True |
| 20484 | True |
| 9814 | True |
| ... | ... |
| 15362 | True |
| 16623 | True |
| 18086 | True |
| 2144 | True |
| 3665 | False |
4128 rows × 1 columns
from sklearn.metrics import confusion_matrixconfusion_matrix(y2_test, y2_pred)array([[1634, 272],
[ 254, 1968]], dtype=int64)from sklearn.metrics import log_loss, jaccard_scorelog_loss(y2_test, y2_pred)4.592771725454366jaccard_score(y2_test, y2_pred)0.789093825180433